Sıfır arasında sıfır belirsizlik (0/0)

Bu yazıda belirsizlik 0/0 veren bir fonksiyonun limitinin nasıl kaydedileceğini açıklıyoruz. Ayrıca sıfırın sıfır arasındaki belirsizliği konusunda çözümlü alıştırmalar yapabileceksiniz.

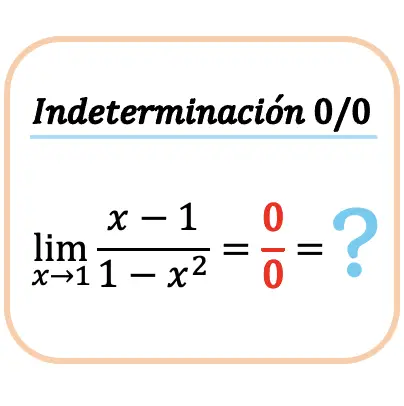
Sıfır (0/0) arasındaki sıfır belirsizliği nasıl çözülür?

Daha sonra sıfır (0/0) arasında sıfır belirsizlik veren bir fonksiyonun limitinin nasıl hesaplanacağını göreceğiz. Bunu yapmak için adım adım bir örnek hesaplayacağız:

\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}

İlk önce x’in değerini fonksiyona koyarak limiti hesaplamaya çalışırız:

\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}

Ancak 0 bölü 0 belirsizliğini elde ederiz.

Bir nokta fonksiyonunun limiti 0/0 belirsizliğini verdiğinde, pay ve paydanın polinomlarını çarpanlara ayırmak ve ardından ortak çarpanları basitleştirmek gerekir.

Bu nedenle kesrin pay ve paydasının polinomlarını çarpanlarına ayırmamız gerekir. Bunu yapmak için Ruffini kuralını kullanıyoruz:

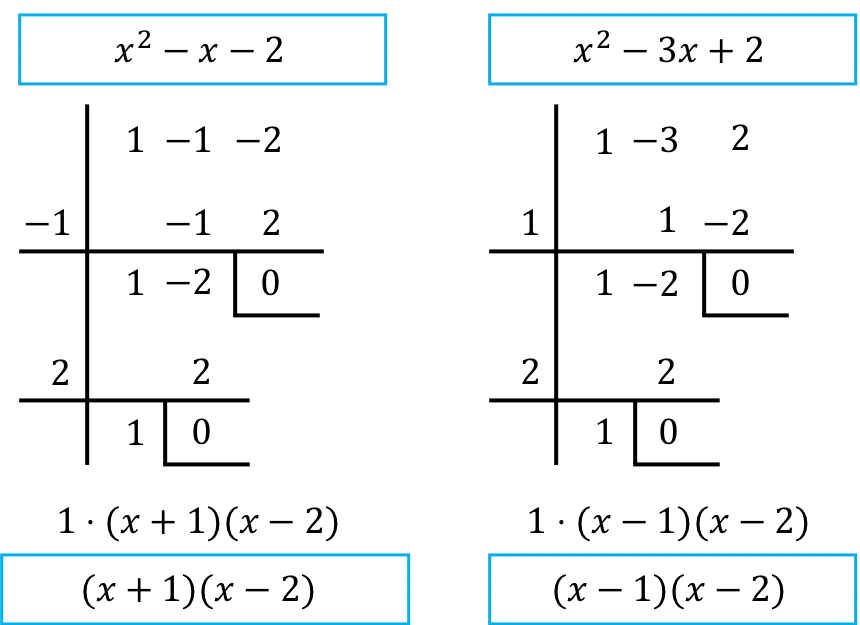
belirsizlik çarpanlarına ayırma 0/0

➤ Bir polinomu nasıl çarpanlara ayıracağınızı bilmiyorsanız polinomlar konusunda uzmanlaşmış sitemizdeki açıklamaya göz atmanızı öneririz: www.polinomios.org

Dolayısıyla polinomlar çarpanlarına ayrıldığında limit aşağıdaki gibidir:

\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}

Artık kesrin pay ve paydasında tekrar eden faktörleri ortadan kaldırarak limiti basitleştirebiliriz:

\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}

Ve son olarak limiti yeniden hesaplıyoruz:

\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}

Gördüğünüz gibi polinomları çarpanlara ayırıp basitleştirdiğimizde limitte çözümü bulmak çok kolay.

Köklerle belirsizlik 0/0

Az önce rasyonel fonksiyonların 0/0 belirsizliklerinin nasıl çözüldüğünü gördük. Ancak limit irrasyonel (veya köklü) bir fonksiyona aitse 0/0 belirsizliği farklı şekilde çözülür.

\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}

Öncelikle aşağıdaki işlemleri gerçekleştirerek limiti çözmeye çalışıyoruz:

\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}

Ancak sıfır üzeri sıfır belirsizliği elde ederiz.

Köklü bir fonksiyonun limiti 0/0 belirsizliği veriyorsa , kesrin pay ve paydasını radikal ifadenin eşleniğiyle çarpmanız gerekir.

➤ Eşleniğin aynı irrasyonel ifade olduğunu ancak ortadaki işaretin değiştirildiğini unutmayın.

Daha sonra kesrin hem payını hem de paydasını radikal ifadenin eşleniğiyle çarpıyoruz:

\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}

Bu tür sınırlar içerisinde bu adımı yaparak her zaman sadeleştirebileceğimiz dikkat çekici bir kimlik elde edeceğiz. Bu durumda paydada bir toplamın ve bir farkın çarpımı bulunur, dolayısıyla:

\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}

\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}

Pay ve paydada tekrarlanan faktörü basitleştiriyoruz:

\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)

Ve bu şekilde limitin sonucunu bulabiliriz:

\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2

Belirsizlikle ilgili çözülmüş alıştırmalar 0/0

Aşağıda 0/0 belirsizlik veren fonksiyonların limitleri üzerine adım adım çözümlü alıştırmalar hazırladık. Bunları yapmayı deneyebilir ve ardından çözümü kontrol edebilirsiniz.

Sınırların çözümü ile ilgili aklınıza takılan tüm soruları bize yorumlarda sorabileceğinizi unutmayın!

1. Egzersiz

Aşağıdaki rasyonel fonksiyonun x=-2 noktasındaki limitini hesaplayın.

\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}

Mantıksal olarak ilk önce limiti çözmeye çalışırız:

\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}

Ancak 0/0 belirsizlikle sonuçlanırız. Bu nedenle pay ve paydanın polinomlarını çarpanlarına ayırmamız gerekir:

\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}

Şimdi pay ve paydada tekrarlanan parantezleri kaldırarak kesri basitleştiriyoruz:

\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}

Ve son olarak limiti basitleştirilmiş kesirle yeniden hesaplıyoruz:

\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}

Alıştırma 2

x -1’e yaklaşırken aşağıdaki fonksiyonun limitini çözün:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}

Öncelikle limiti her zamanki gibi çözmeye çalışıyoruz:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}

Ancak 0 arasında 0 belirsizliğini elde ederiz. Bu nedenle kesrin 2 polinomunu çarpanlarına ayırmamız gerekir:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}

Artık polinomları basitleştirebiliriz:

\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}

Ve limiti çözüyoruz:

\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}

Alıştırma 3

Aşağıdaki radikal fonksiyonun limitinin çözümünü belirleyin:

\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}

Öncelikle limitin bir tür belirsizlik verip vermediğini kontrol ediyoruz:

\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}

Limit, sıfırın sıfıra bölünmesiyle oluşan belirsizliği verir ve fonksiyonda bir kökümüz vardır. Bu nedenle kesrin payını ve paydasını radikal ifadenin eşleniğiyle çarpmamız gerekir:

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}

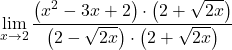
Payda, bir toplam ve bir farkın çarpımının dikkate değer kimliğinin gelişimine karşılık gelir, bu nedenle onu basitleştirebiliriz:

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}

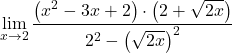
Ancak kesrin terimlerini henüz basitleştiremiyoruz. Bu nedenle polinomları çarpanlarına ayırmalıyız:

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}

Bu şekilde kesri sadeleştirebiliriz:

\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}

Artık limitin sonucunu belirleyebiliriz:

\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}

Alıştırma 4

Aşağıdaki radikal fonksiyonun x’i 0’a yaklaşırken limitini hesaplayın:

\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}

Öncelikle her zaman yaptığımız gibi fonksiyonun limitini hesaplamaya çalışıyoruz:

\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}

Ama 0/0’ın belirsiz biçimini elde ederiz. Bu nedenle, fonksiyonun payını ve paydasını irrasyonel ifadenin eşleniğiyle çarpıyoruz:

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}

Paydayı basitleştirmek için karşılık gelen dikkate değer kimlik formülünü uyguluyoruz:

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}

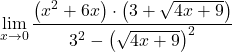
Şimdi ortak çarpanı alarak payın binomunu çarpanlarına ayırıyoruz:

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}

Fonksiyonun pay ve paydasında tekrarlanan faktörleri basitleştiriyoruz:

\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}

Ve son olarak fonksiyonun limitini çözüyoruz:

\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}

Alıştırma 5

0/0 belirsizlik yöntemini kullanarak aşağıdaki limiti çözün:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}

➤ Bakınız: bir fonksiyonun yanal limitleri nasıl hesaplanır

İlk önce limiti çözmeye çalışıyoruz:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}

Ancak limitte sıfıra sıfır belirsizliği elde ederiz. Bu nedenle pay ve paydanın polinomlarını çarpanlara ayırıyoruz:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}

Şimdi pay ve paydada tekrar eden faktörleri ortadan kaldırarak kesri basitleştiriyoruz:

\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}

Ve limiti tekrar hesaplıyoruz:

\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty

Ama şimdi kendimizi 0’a bölünen bir sayının belirsizliğiyle karşı karşıya buluyoruz. Dolayısıyla x -1’e doğru gittiğinde fonksiyonun yanal limitlerini hesaplamamız gerekiyor.

İlk önce fonksiyonun soldaki x=-1 noktasındaki yanal limitini çözüyoruz:

\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty

Daha sonra sağdaki x=-1 noktasında fonksiyonun yanal limitini hesaplıyoruz:

\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty

Bu nedenle, iki yanal limit çakışmadığı için fonksiyonun x=-1 noktasındaki limiti mevcut değildir:

\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top