Newton’un binom’u, belirli bir kuvvete yükseltilen iki terimin toplamını ifade etmek için kullanılan matematiksel bir formüldür. Adını İngiliz matematikçi Isaac Newton’dan alan bu formül matematiğin birçok alanında kullanılmaktadır.
Örneğin istatistikte, olasılık teorisinde ve diferansiyel ve integral hesapta faydası vardır. Binom teoremi, bir binomun gücünü basit bir şekilde hesaplamamızı sağlar.
Basitçe söylemek gerekirse, Newton’un binom’u , (a+b) n biçimindeki herhangi bir cebirsel ifadenin çözülebileceği bir formüle dayanmaktadır. Bu formül ismini Isaac Newton’dan alsa da kökeni konusunda tartışmaların olduğunu da belirtmekte fayda var.
Yani bazı araştırmalar binom teoreminin Orta Doğu’daki kullanımını bulmayı öneriyor.
Newton’un iki terimlisi ne zaman geliştirildi?
Newton’un binom teoremi, aynı zamanda Newton’un binom’u olarak da bilinir, 1665’te geliştirildi ve ilk olarak 1676’da Kraliyet Cemiyeti memurundan iki mektupla iletildi .
Bu mektuplar, sonsuz serilere ilişkin matematiksel araştırmaları daha iyi anlamaya çalışan Alman matematikçi Gottfried Wilhelm von Leibniz’e bir yanıttı. Newton teoreminin sonuçlarını paylaştı ve Leibniz bunun karesel veya serilerde sonuç elde etmek için yararlı bir teknik olduğunu fark etti.
Bu gözlem, Newton’un , sonlu polinom ifadeleriyle aynı şekilde sonsuz seriler üzerinde çalışmanın mümkün olduğu sonucuna varmasını sağladı. Newton teoremini hiçbir zaman yayınlamamasına rağmen, İngiliz matematikçi John Wallis bunu 1685’te Cebir’inde yayınladı ve yaratılışını Newton’a bağladı.
Buna neden Newton’un binom adı veriliyor?
Newton’un iki terimlisi, adını onu 17. yüzyılda geliştiren İngiliz matematikçi ve fizikçi Isaac Newton’dan almıştır. Newton bu teoremi keşfeden ilk kişi değildi ama herhangi bir pozitif n tamsayısı için geçerliliğini kanıtlayan ilk kişi oydu.
Newton’un binom’u cebir ve matematikte çok kullanışlı bir matematik aracıdır ve fizik, istatistik, mühendislik ve bilgisayar bilimi gibi alanlarda yaygın olarak kullanılır.
Newton’un binom formülü nedir?
Daha önce de belirttiğimiz gibi Newton’un binom’u, bir binomun kuvvetlerinin bulunabileceği formüldür. Söz konusu binom kuvvetini bulmak için “binom katsayıları” kullanılır. Önceki terim kombinasyon dizilerini ifade eder.
Bunu aklımızda tutarak Newton’un binom formüllerini şu şekilde parçalayabiliriz:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = a 3 + 3a 2 b + 3 ab 2 + b 3
(a+b) n’nin gelişimini ifade eden matematiksel ifadelere dikkate değer varlıklar denir ve herhangi bir “n” doğal sayısı için bu işlemi temsil eden genel bir formülün elde edilmesini mümkün kılar.
Ortaya çıkan her polinomun katsayılarını inceleyerek Pascal Üçgeni olarak bilinen diziyi takip eden bir dizi fark edebiliriz.
Pascal üçgeninin dizisi 1 rakamıyla başlar ve takip eden her satırda son rakamlar her zaman 1 olur. Ara değerler, bir önceki satırda hesaplanacak değerin hemen üzerindeki iki rakamın eklenmesiyle elde edilir.
Newton’un binomunda bir terim nasıl bulunur?
Newton binomunda belirli bir terimi bulmak için genel formül kullanılır:
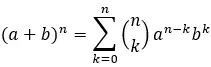
Altın:
a ve b binomun katsayılarıdır.
n, binomun üssüdür.
k bulmak istediğimiz spesifik terimdir.
Σ k=0’dan n’ye toplamını temsil eder.
[nk] aşağıdaki formülle hesaplanan binom katsayısıdır:
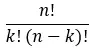
Bu nedenle, tamamen genişletilmiş formül şu şekildedir:
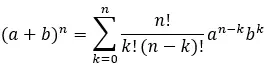
Çözülmüş Newton binom örneği
Bu değerler bulunduktan sonra formülde yerine konulur ve ifade çözülerek belirli bir terim elde edilir. Örneğin, (2x + 3) 6 binomunun beşinci terimini bulmak istersek şunu elde ederiz:
bir = 2x
b = 3
n=6
k = 5
Yani, formülü kullanarak:
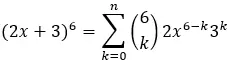
Beşinci terim k=5’e karşılık gelir, dolayısıyla elimizde:
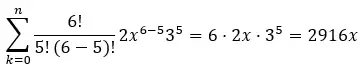
Dolayısıyla (2x + 3) 6 binomunun beşinci terimi 2916x’tir.
5. dereceden Newton binom değeri nedir?
Derecesi 5 olan bir Newton iki terimlisi, (a + b) 5 formunun cebirsel bir ifadesidir; burada “a” ve “b” değişkenlerdir ve üstel 5, iki terimlinin derecesini gösterir . Bu ifadeyi genişleterek altı terimi olan ikinci dereceden bir polinom elde ederiz:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Bu polinomun her terimi, binomun katsayılarının “a” ve “b” kuvvetleriyle birleştirilmesiyle elde edilir. Örneğin ikinci terim (5a 4 b), binom katsayısının (5 seç 1 = 5) dördüncü kuvvetine yükseltilmiş “a” ve birinci kuvvetine yükseltilmiş b ile çarpılmasıyla elde edilir.
Newton’un 5. derece binomları istatistik, olasılık teorisi ve kuantum mekaniği gibi matematik ve fiziğin farklı dallarında faydalıdır.
Newton binomunun uygulamaları nelerdir?
Newton’un binomunun çeşitli alanlarda geniş bir uygulama yelpazesi vardır:
- Olasılıkların hesaplanması : Binom teoremi, yazı tura atılması veya bir dizi testin başarısı veya başarısızlığı gibi binom olaylarının olasılıklarını hesaplamak için kullanılır.
- Sayı Teorisi – Newton’un binom’u, sayı teorisindeki polinomları genişletmek ve denklemleri basitleştirmek için kullanılır.
- İstatistik : Newton’un binom’u, binom dağılımlarını hesaplamak ve güven aralıklarının oluşturulmasında kullanılır.
- Fizik – Fizikte, binom teoremi diğer alanların yanı sıra görelilik teorisinde ve kuantum mekaniğinde kullanılır.
- Ekonomi ve Finans : Newton binomili, nakit akışlarının zaman içindeki mevcut ve gelecekteki değerini hesaplamak ve finansal opsiyonların değerlemesinde kullanılır.
- Programlama ve bilgisayar bilimi : Newton’un iki terimlisi algoritma geliştirmede ve bilgisayar programlamada kullanılır.
Newton’un binom’u neden önemlidir?
Newton’un iki terimlisi konuyla ilgilidir çünkü cebir ve sayılar teorisinin gelişimi için temel bir matematiksel araçtır. Denklemleri çözmek ve cebirsel ifadeleri basitleştirmek için çok yararlı olan, kare alma işleminin sonucunu veya bir binomun diğer herhangi bir kuvvetini hesaplamanıza olanak tanır.
Ayrıca istatistik, olasılık ve fizik gibi alanlarda da uygulamaları vardır. Özetle, Newton’un iki terimlisi matematikte önemli bir kavramdır ve bunu anlamak birçok çalışma alanında ilerlemek için çok önemlidir.
Newton’un binomunu ifade etmenin başka yolları var mı?
Evet, Newton binomunu ifade etmenin başka yolları da var. Örneğin, kombinatoryal gösterim kullanılarak binom katsayıları cinsinden ifade edilebilir.
Ayrıca Euler formülü kullanılarak üstel fonksiyonlar ve trigonometrik fonksiyonlar cinsinden de ifade edilebilir. Benzer şekilde, Legendre formülünü kullanarak gama fonksiyonu açısından. Bu alternatif ifadeler farklı bağlamlarda ve matematik problemlerinde faydalı olabilir.
Newton Binom Örnekleri
Daha sonra Newton binomunun bazı basit uygulama örneklerini görelim.
Örnek 1: (x + y) 5 açılımında 3. dereceden terimi hesaplayın.
Çözüm: (x + y) 5 açılımında birinci terimin katsayısı 1, ikinci terimin katsayısı 5, üçüncü terimin katsayısı 10, dördüncü terimin katsayısı 10, Beşinci terimin katsayısı 5, altıncı terimin katsayısı ise 1’dir.
Bu nedenle 3. derecenin terimi:
10×2 ve 3
Örnek 2: (2x – 1) 4 açılımındaki bağımsız terimi bulun.
Çözüm: (2x – 1) 4 açılımında bağımsız terim (2x) p (-1) (4-p) kombinasyonunda bulunur; burada p, (2x) p’nin üssünü yapan değerdir ve (-1) (4-p) toplamı 4 eder.
Dolayısıyla bağımsız terim şu şekildedir:
(2x) 2 (-1) 2 = 4
Örnek 3: (3x – 2y) 6 açılımındaki en yüksek dereceli terimi bulun.
Çözüm: (3x – 2y) 6 açılımındaki en yüksek dereceli terim (3x) p (-2y) (6-p) kombinasyonunda bulunur; burada p, (3x) p’nin üssünü yapan değerdir ve (-2y) (6-p), binomun derecesine eşittir, yani 6.
Bu nedenle en yüksek dereceli terim:
(3x) 3 (-2y) 3 = -216x 3 ve 3