▷ Ters veya karşılıklı fonksiyon nasıl bulunur (çözülmüş alıştırmalar)

Bu makalede ters (veya karşılıklı) fonksiyonun ne olduğunu ve bir fonksiyonun tersinin nasıl hesaplanacağını açıklıyoruz. Ayrıca bir fonksiyonun tersinin olup olmadığını ve bu tür fonksiyonların özelliklerini nasıl kolayca anlayacağınızı da keşfedeceksiniz. Son olarak ters fonksiyonlarla ilgili adım adım alıştırmalar yapabilirsiniz.

Ters fonksiyon nedir?

Karşılıklı fonksiyon olarak da adlandırılan ters fonksiyon, tanım kümesi başka bir fonksiyonun (orijinal fonksiyon) aralığı ve aralığı orijinal fonksiyonun tanım kümesi olan fonksiyondur. f fonksiyonunun ters fonksiyonu f ^-1 sembolüyle ifade edilir.

Dolayısıyla f(x)’ in ters fonksiyonu aşağıdaki koşulu sağlayan fonksiyondur:

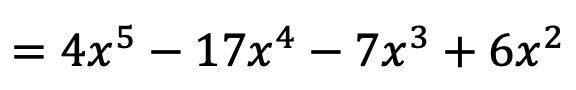
Altın

$f^{-1}$

ters fonksiyonudur

$f.$

Ters fonksiyon kavramı, fonksiyon bileşimi kullanılarak da tanımlanabilir, çünkü ters fonksiyonuyla oluşturulan herhangi bir fonksiyon, birim fonksiyona eşittir:

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

➤ Bakınız: fonksiyon bileşimi nedir?

Yani eğer önceki denklem yerine getirilirse, bu şu anlama gelir:

$f^{-1}$

ters fonksiyonudur (veya karşılıklı fonksiyondur)

$f.$

Ters fonksiyon örneği

Ters fonksiyonun tanımını verdikten sonra anlamını daha iyi anlamak için bir örnek çözelim.

Aşağıdaki fonksiyonların birbirinin tersi olup olmadığını belirleyin:

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Eğer iki fonksiyon birbirinin tersi ise aşağıdaki 2 koşul karşılanacaktır:

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Şimdi her iki denklemin de sağlanıp sağlanmadığını kontrol edelim. İlk önce kontrol ediyoruz

$(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

➤ Eğer az önce yaptığımız hesaplamayı anlamadıysanız yukarıdaki Fonksiyonların bileşimi nedir? bağlantısına gitmeniz gerekmektedir. Bu tip işlemleri fonksiyonlarla nasıl çözebileceğimizi açıklıyoruz.

Böylece

$(f \circ g)(x) = x$

evet gerçekleşti. ✅

Şimdi eşitliği kontrol edelim

$(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

Ve tersinirlik koşulu

$(g \circ f)(x) = x$

o da başarılmıştır. ✅

Sonuç olarak, her iki denklem de geçerli olduğundan, iki fonksiyon birbirinin tersidir.

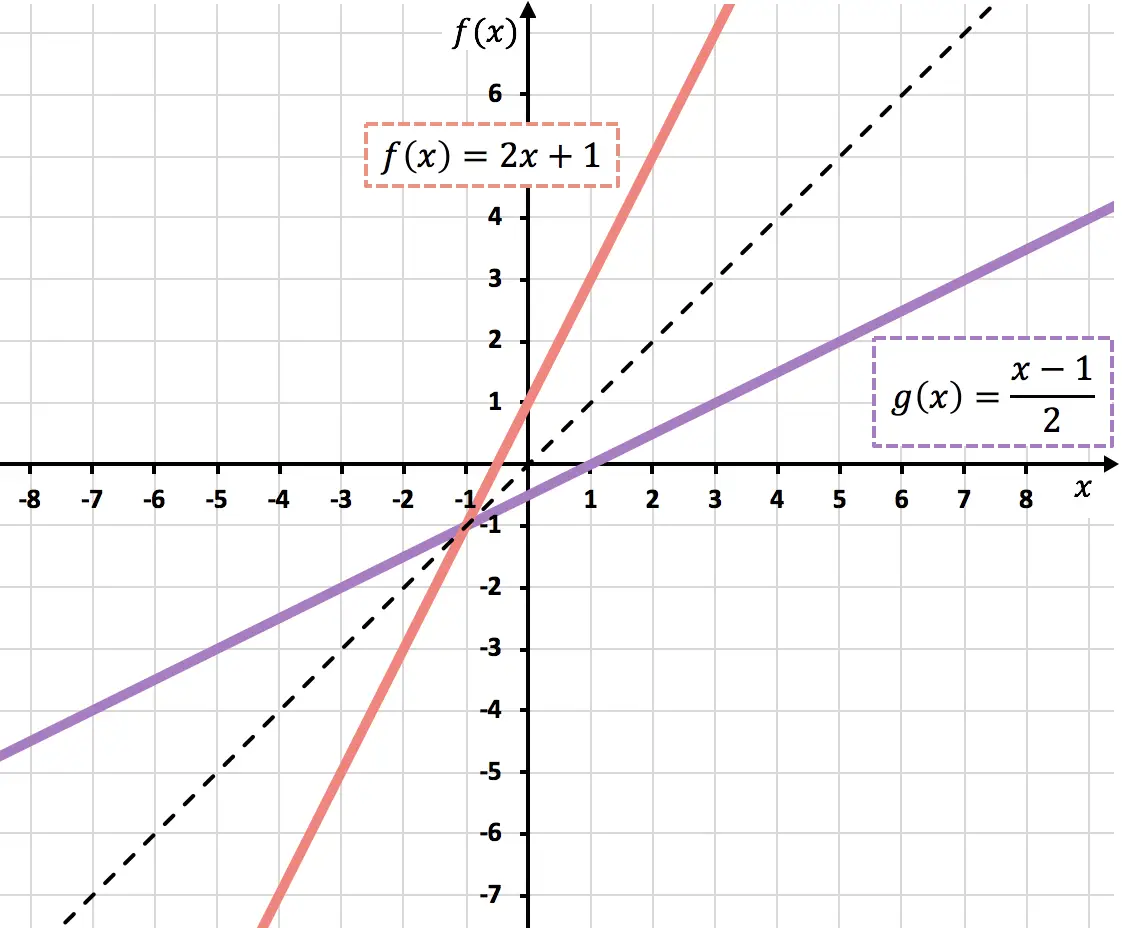
Aşağıda her iki fonksiyonun grafiğini görebilirsiniz. İki ters fonksiyonun grafiklerinin birinci ve üçüncü çeyreğin açıortaylarına göre simetrik olduğuna dikkat edin:

Bir fonksiyonun tersi olup olmadığı nasıl anlaşılır

Bir fonksiyon, eğer bir birebir fonksiyonsa, yani tüm etki alanındaki her değer, kendi aralığındaki tek bir değere karşılık geliyorsa, bir ters fonksiyona sahiptir .

Ters fonksiyonlu üstel fonksiyon

Ters fonksiyonu olmayan ikinci dereceden fonksiyon

Örneğin, sol üstel fonksiyonun bir ters fonksiyonu vardır çünkü her x , f(x) ‘in tek bir değerine karşılık gelir. Öte yandan, sağ ikinci dereceden fonksiyon, görüntüleri eşit olan birkaç x değerine sahip olduğundan ters bir fonksiyona sahip değildir (örneğin f(1)=f(3)=2) .

Benzer şekilde, bir öznel işlev hem birebir hem de örten bir işlevden oluşur, dolayısıyla herhangi bir öznel işlev aynı zamanda bir ters işleve de sahiptir.

Öte yandan, ters fonksiyonun bir fonksiyonun çarpımlı tersiyle aynı şey olmadığını, iki farklı kavram olduğunu unutmamalısınız. Bir fonksiyonun çarpımsal tersini bulmak için, söz konusu fonksiyonun 1 karşılığını hesaplamanız yeterlidir.

$f^{-1}(x) \neq \cfrac{1}{f(x)}$

Bir sonraki bölümde ters fonksiyonun nasıl belirleneceğini göreceğiz.

Ters fonksiyon nasıl bulunur

Bir fonksiyonun tersini hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

f(x)’ i y ile değiştirin.
Tüm x’i y olarak değiştirin ve bunun tersi de geçerlidir.
Y değişkenini temizleyin.
Y değişkenini f ^-1 (x) ile değiştirin. Ters fonksiyon f ^-1 (x) için bulunan ifadedir.

Ters fonksiyonun nasıl hesaplandığını tam olarak görebilmeniz için örnek olarak aşağıdaki fonksiyonun tersini belirleyeceğiz:

$f(x) =4x+5$

Öncelikle değiştirmemiz gerekiyor

$f(x)$

İçin

$y$

$y=4x+5$

Şimdi her şeyi değiştiriyoruz

$x$

tarafından fonksiyonun

$y$

ve tam tersi:

$y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5$

Daha sonra değişkeni temizliyoruz

$y:$

$x=4y+5$

$x-5=4y$

$\cfrac{x-5}{4}=y$

$y=\cfrac{x-5}{4}$

Ve son olarak ters fonksiyon

$f(x)$

izole ederek elde ettiğimiz cebirsel ifadedir

$y:$

$\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}$

Ters fonksiyonla ilgili çözülmüş alıştırmalar

Aşağıda, pratik yapabilmeniz için ters fonksiyonla ilgili birkaç adım adım alıştırma hazırladık.

👉Bir egzersizin nasıl çözüleceğini anlamadıysanız ya da sizin için bir problemi çözmemizi istiyorsanız yorumlarda bize yazabileceğinizi unutmayın!

1. Egzersiz

Aşağıdaki iki fonksiyonun ters (veya karşılıklı) olup olmadığını kontrol edin:

$f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}$

Çözümü görün

İki fonksiyonun birbirinin tersi olması için aşağıdakilerin doğru olması gerekir:

$(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x$

Bu nedenle iki koşulun karşılanıp karşılanmadığını kontrol etmek gerekir. İlk önce kontrol ediyoruz

$(f \circ g)(x)=x :$

$\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}$

Henüz,

$(f \circ g)(x) = x$

evet gerçekleşti. ✅

Şimdi diğer fonksiyon bileşimini kontrol edelim

$(g \circ f)(x)=x :$

$\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}$

Vasıtasıyla

$(g \circ f)(x) = x$

o da başarılmıştır. ✅

Bu nasıl oluyor

$(f \circ g)(x)=x$

$(g \circ f)(x)=x$

, iki fonksiyon birbirinin tersidir.

Alıştırma 2

Aşağıdaki birinci dereceden polinom fonksiyonunun tersini (veya karşılıklı fonksiyonunu) hesaplayın:

$f(x)=-2x-3$

Çözümü görün

Fonksiyonu tersine çevirmek için yapılacak ilk şey terimi değiştirmektir.

$f(x)$

İçin

$}y:$

$y=-2x-3$

Şimdi değiştiriyoruz

$x$

ile

$y$

ve tam tersi:

$y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3$

Ve sonra serbest bırakıyoruz

$y:$

$x =-2y-3$

$x +3=-2y$

$\cfrac{x +3}{-2}=y$

$y = \cfrac{x +3}{-2}$

Zaten yayınlamayı başardık

$y$

. Bu nedenle, ters fonksiyon

$f(x)$

Doğu:

$\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}$

Alıştırma 3

Aşağıdaki ikinci dereceden polinom fonksiyonunu ters çevirin:

$f(x)=x^2-1$

Çözümü görün

Ters fonksiyonu bulmak için yukarıda gördüğümüz prosedürü takip edeceğiz. Bu yüzden arayacağız

$y$

fonksiyona

$f(x):$

$y=x^2-1$

İkincisi, değiştiriyoruz

$x$

için

$y$

ve tam tersi:

$y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1$

Ve son olarak değişkeni izole ediyoruz

$y:$

$x =y^2-1$

$x+1=y^2$

$\sqrt{x+1}=y$

$y=\pm \sqrt{x+1}$

Ancak bu durumda elde edilen fonksiyon, etki alanının her elemanı için iki görüntüye sahiptir (pozitif görüntü ve negatif görüntü). Bu nedenle problem fonksiyonunun ters fonksiyonu yoktur .

Alıştırma 4

Aşağıdaki rasyonel fonksiyonun ters fonksiyonunu (veya karşılıklı fonksiyonunu) belirleyin:

$\displaystyle f(x)=\frac{x-1}{2x+3}$

Çözümü görün

İlk önce değiştiriyoruz

$f(x)$

İçin

$y:$

$y=\cfrac{x-1}{2x+3}$

Şimdi değiştiriyoruz

$x$

pay ve payda

$y$

ve tam tersi:

$y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}$

Ve sonra serbest bırakıyoruz

$y:$

$x=\cfrac{y-1}{2y+3}$

İfade

$2y +3$

Denklemin sağ tarafının tamamını böldüğü için bunu denklemin sol tarafının tamamını çarparak çarpabiliriz:

$x\cdot (2y+3)=y-1$

$2yx+3x=y-1$

Tüm şartları koyuyoruz

$y$

Denklemin bir tarafında, diğer terimler diğer tarafında:

$2yx-y=-3x-1$

Temizlemek için

$}y$

denklemin sol tarafından ortak faktörü çıkarıyoruz:

$y(2x-1)=-3x-1$

Ve bir postacı olarak

$(2x-1)$

denklemin sol tarafının tamamını çarpmak, bunu sağ tarafın tamamını bölerek yapabiliriz:

$y=\cfrac{-3x-1}{2x-1}$

Zaten yayınlamayı başardık

$y$

. Yani ters fonksiyonu

$f(x)$

Doğu:

$\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}$

Ters fonksiyonun özellikleri

Ters fonksiyon aşağıdaki özelliklere sahiptir:

Ters fonksiyon benzersizdir, yani bir fonksiyon tersinebilirse, bu fonksiyon için yalnızca bir ters fonksiyon vardır.

Ters fonksiyonun alanı orijinal fonksiyonun aralığıdır (veya aralığıdır).

Benzer şekilde, ters fonksiyonun yolu da orijinal fonksiyonun tanım kümesine eşdeğerdir.

Ters fonksiyonundan oluşan herhangi bir fonksiyon, özdeşlik fonksiyonunu (x) verir.

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

Bir fonksiyonun grafiği ile ters fonksiyonunun grafiği birinci ve üçüncü çeyreğin ortaortasına göre simetriktir.

Ters fonksiyonun tersi orijinal fonksiyona eşittir:

$\left(f^{-1}\right)^{-1}=f$

Bileşik bir fonksiyonun ters çevrilmesi, her fonksiyonun tersinin ayrı ayrı hesaplanmasına ve ardından ters fonksiyonların oluşturulmasına eşdeğerdir.

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Bir fonksiyon, ters fonksiyonuyla aynı anda süreklidir, yani bir fonksiyon sürekliyse ters fonksiyonu da sürekli olacaktır.

Bir fonksiyon türevlenebilirse ve türevi hiçbir zaman kaybolmuyorsa
$f'(x)\neq 0$

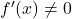
ters fonksiyonu da türevlenebilir olacaktır.

Ek olarak ters fonksiyonun türevi, formülü aşağıdaki gibi olan ters fonksiyon teoremi uygulanarak hesaplanabilir:

$\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}$

Ters (veya karşılıklı) fonksiyon

Ters fonksiyon nedir?

Ters fonksiyon örneği

Bir fonksiyonun tersi olup olmadığı nasıl anlaşılır

Ters fonksiyon nasıl bulunur

Ters fonksiyonla ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Ters fonksiyonun özellikleri

Yorum bırakın Yanıtı iptal et