Euler sayısı (Euler sabiti olarak da bilinir), sayı teorisi, topoloji, grup teorisi ve fonksiyon teorisi dahil olmak üzere matematiğin çeşitli alanlarında önemli ve temel bir matematiksel sayıdır. Yunanca “e” harfi ile temsil edilir ve yaklaşık değeri 2,71828’dir.
e sayısı üstel fonksiyonun formülünden gelir ve karmaşık sayılar teorisinde temel bir sayıdır.
Aynı zamanda olasılık hesaplaması ve büyüme ve bozulma süreçlerinin modellenmesi de dahil olmak üzere birçok matematik probleminin çözümünde ortaya çıkan bir doğal sayıdır.
Euler sayısının kökeni nedir?
Euler sayısı, adını tüm zamanların en büyük matematikçilerinden biri olan ve modern matematiğin babası olarak kabul edilen İsviçreli matematikçi Leonhard Euler’den (1707-1783) almaktadır.
Euler, sayılar teorisi, geometri, matematik, fizik ve astronomi dahil olmak üzere matematiğin birçok alanına değerli katkılarda bulundu.
Logaritmaların hesaplanması ve teorisi üzerine yaptığı çalışmada e sayısını (Euler sayısı olarak adlandırılır) ilk tanımlayan ve kullanan kişi oydu. Euler’in karmaşık sayılara ilişkin formülü aynı zamanda onun matematiğe en önemli katkılarından biridir.
Bu değer nasıl elde ediliyor?
Aslında Euler sayısını hesaplamanın birkaç yöntemi vardır. Ancak her iki yöntemin de kesin bir sonuç vermediğini belirtmekte fayda var. Dolayısıyla numaralandırması sürekli ve sonsuzdur ancak tekrarlanmaz.
Aslında şu anda e sayısını oluşturan 1 trilyondan fazla sayı bilinmektedir. Euler sayısını tanımlayan sonsuz seri:

Altın “!” o sayıya kadar olan tüm doğal sayıların çarpımı olarak tanımlanan faktöriyeldir. Örneğin:
5! = 5 4 3 2 1 = 120
Bu seriyi grafiksel olarak yüksekliği 1 ve azalan genişliği olan bir dizi dikdörtgenin toplamı olarak görebiliriz; burada her dikdörtgenin genişliği 1/n!’dir; burada n, faktöriyellerin sayısıdır.
Toplamdaki dikdörtgen sayısını arttırırsak üstel fonksiyonun eğrisinin altındaki alanın yaklaşımı Euler sayısına giderek yaklaşır.
Özetle Euler sayısı sonsuz bir serinin toplamından elde edilen ve matematiğin birçok alanı için temel olan bir sayıdır. İrrasyonel bir sayı olmasına rağmen yaklaşık değeri 2,71828’dir.
Euler’in e’den 18’e kadar olan basamağı hesaplamak için bu yöntemi kendisinin uyguladığını akılda tutmak önemlidir.
Bunu hesaplamanın başka bir yolu:
Euler sayısının bir doğru üzerindeki yaklaşık değerini bir dizi sonlu terim kullanarak hesaplayabiliriz. Örneğin yukarıda tanımlanan ilk sonsuz seriyi alırsak:

Serinin ilk terimlerini toplayarak yaklaşık değeri hesaplayabiliriz. Örneğin ilk 6 terimi toplarsak:
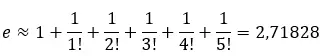
Bu seriyi bir doğru üzerinde çizerek yaklaşık 2,71828 değerine nasıl yaklaştığını görebiliriz.
Grafiksel olarak, Euler sayısını temsil eden çizgi, yüksekliği 1 ve azalan genişliği olan bir dikdörtgenler dizisi olarak çizilebilir; burada her dikdörtgenin genişliği 1/n!’dir; burada n, faktöriyellerin sayısıdır.
Toplamdaki dikdörtgen sayısını arttırırsak üstel fonksiyonun eğrisinin altındaki alanın yaklaşımı Euler sayısına giderek yaklaşır.
Euler sayısıyla üstel denklemler
Euler sayısına sahip üstel denklemler, diğerlerinin yanı sıra fizik, biyoloji, ekonomi gibi bilimlerdeki çok çeşitli olguları modellemek için kullanılabilir. İşte bazı örnekler:
Üstel büyüme ve bozulma
Bu model, bir popülasyonun büyüme veya azalma hızını veya toksik bir maddenin parçalanma hızını açıklar.
Örneğin, eğer bir popülasyon yılda %5 oranında artıyorsa, büyüklüğü şu formülle açıklanabilir:
P(t) = P0 · e 0,05t , burada P0 başlangıç popülasyon büyüklüğüdür.
Radyoaktif bozunma modelleri
Bu model, radyoaktif atomların zaman içinde bozunma hızını açıklar.
Formül aşağıdaki gibidir:
N(t) = N0 e -λt
burada N0 başlangıçtaki atom sayısıdır, λ radyoaktif malzemeye bağlı bir sabittir ve t zamandır.
Bunlar Euler sayılı üstel denklemlerin pratikte nasıl kullanılabileceğine dair sadece birkaç örnektir . Üstel denklemlerin kullanışlı ve alakalı olduğu başka birçok alan vardır.
Euler sayısının uygulamaları nelerdir?
Euler sayısının matematik ve bilimin farklı alanlarında geniş bir uygulama alanı vardır. e sayısının kullanıldığı alanlardan bazıları şunlardır:
- Hesaplama ve matematiksel analiz : Üstel ve logaritmik fonksiyonların incelenmesinde ve diferansiyel denklemlerin çözümünde kullanılır.
- Sayı teorisi – asal sayıların dağılımının incelenmesinde ve sayı teorisiyle ilgili problemlerin çözümünde kullanılır.
- Olasılık ve İstatistik : Olasılık dağılımı ile ilgili problemlerin çözümünde ve beklenen değerlerin tahmin edilmesinde kullanılır.
- Kriptografi – Şifreleme ve şifre çözme algoritmalarının incelenmesinde kullanılır.
- Fizik – termodinamik, kuantum mekaniği ve istatistiksel fizikle ilgili problemleri çözmek için kullanılır.
- Kimya : Kimyasal termodinamik ve kimyasal kinetiğe ilişkin problemlerin çözümünde kullanılır.
Karmaşık sayılar için Euler formülü
Euler’in karmaşık sayılara ilişkin formülü, trigonometrik ve üstel fonksiyonlar arasında bir ilişki kurar. Formül şöyle yazılmıştır:

Burada “e” doğal logaritmanın tabanını, “i” sanal birimi, “x” gerçek bir sayıyı ve “cos” ve “sin” sırasıyla kosinüs ve sinüs trigonometrik fonksiyonlarıdır.
Bu formül, sayılar teorisi, fonksiyon teorisi ve karmaşıklık teorisi dahil olmak üzere matematiğin birçok alanında çok faydalıdır ve mühendislik, fizik ve ekonomide çok çeşitli uygulamalara sahiptir.
Kullanımının pratik bir örneği, periyodik sinyallerin karmaşık sinüzoidal sinyallerin toplamı olarak temsil edildiği Fourier analizindeki sinyal ve sistemlerin temsilidir .
Euler formülü, bu karmaşık sinyallerin, bireysel sinüzoidal sinyalleri tanımlayan gerçek trigonometrik fonksiyonlarla nasıl ilişkili olduğunu açıklamak için kullanılır.
Euler sayısı ve bileşik faiz
Bileşik faiz, anapara adı verilen bir miktar paranın, zamanla artan faiz üzerinden faiz kazanması sürecini tanımlayan finansal bir kavramdır .
Yani bir yatırımdan kazanılan faiz sadece başlangıç sermayesinden değil aynı zamanda geçmiş dönemlerde kazanılan faizlerden de gelir.
Euler sayısı ve bileşik faiz ilişkilidir çünkü bileşik faizi hesaplamak için kullanılan formül Euler sayısını kullanır. Bileşik faizin formülü şu şekildedir:
A = P e rt
A nihai tutar, P ana para, r faiz oranı, t zaman ve e Euler sayısıdır. Bu şekilde Euler sayısı, bileşik faizin hesaplanmasına yönelik matematiksel formülasyonda önemli bir faktördür.
Bileşik faizin somut sayılarla hesaplanmasına bir örnek şöyle olabilir:
2 yıl boyunca yıllık %5 faiz oranıyla 1.000 € tutarında bir yatırımımız olduğunu varsayalım. Bileşik faizi hesaplamak için formül şöyle olacaktır:
A = P e rt = 1000 e 0,05 2 = 1000 1,1025 = 1102,5 €.
Bu, 2 yıl sonra oluşan bileşik faiz sayesinde 1.000€’luk başlangıç sermayemizin 1.102,5€’ya yükseleceği anlamına geliyor.
Euler sayısıyla matematik alıştırmalarına örnekler
Euler sayısını içeren çözülmüş matematik problemlerinin iki örneği:
1. X’in bir gerçel sayı olduğu “e ix ” değerini bulun:
Euler’in özdeşliği bize e ix = cos(x) + i · sin(x) olduğunu söyler. Dolayısıyla x’in değerini biliyorsak e ix’in değerini trigonometrik fonksiyonları kullanarak hesaplayabiliriz.
2. Belirli bir x değeri için e^(x 2 ) değerini hesaplayın:
e^(x 2 ) değerini hesaplamak için Taylor serisini kullanabiliriz. Taylor serisi e x, kullanılan terime bağlı olarak e x’in değerinin ardışık yaklaşımlarını hesaplamayı mümkün kılan sonsuz bir genişlemedir.

Bu seride x’in yerine x2 koyarsak e^( x2 ) için Taylor serisini elde ederiz.