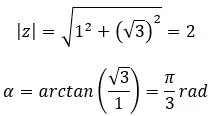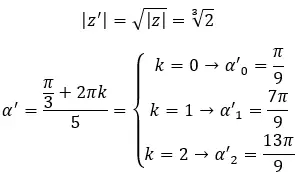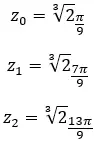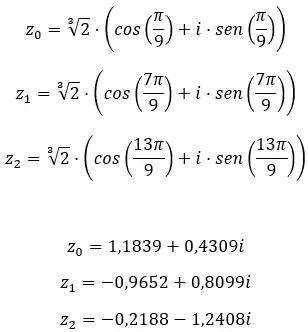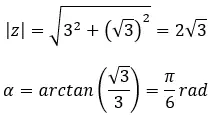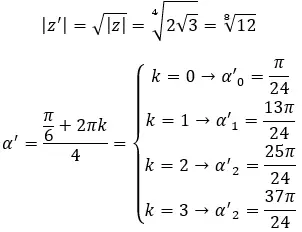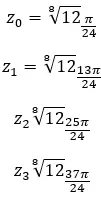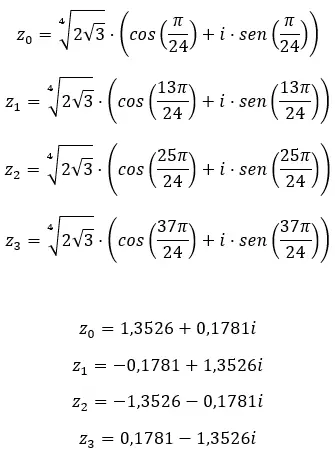Karmaşık sayıların köklerini hesaplamak oldukça basittir. Prosedürü bir kez anladığınızda, oldukça tekrarlayıcı oluyor. Daha sonra bunu açıklayacağız ve size bir örnek vereceğiz, böylece bunu gerçek egzersizlerde nasıl uygulayacağınızı öğrenebilirsiniz.
karmaşık sayıların n’inci kökleri
N’inci kök kavramı, n’inci dereceden kök demekle eşdeğer olduğundan, bir karmaşık sayının karekökünü ve beşinci kökünü hesaplamak için aynı yöntem kullanılır. Elbette bu sıraya göre çözüm sayısı da değişecektir.
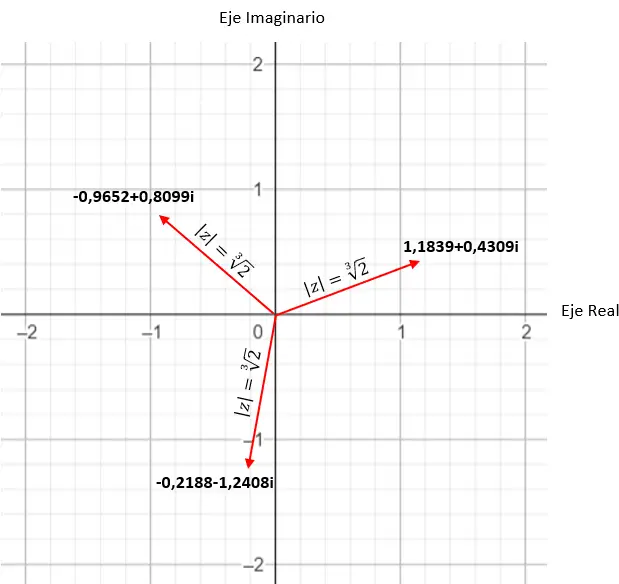
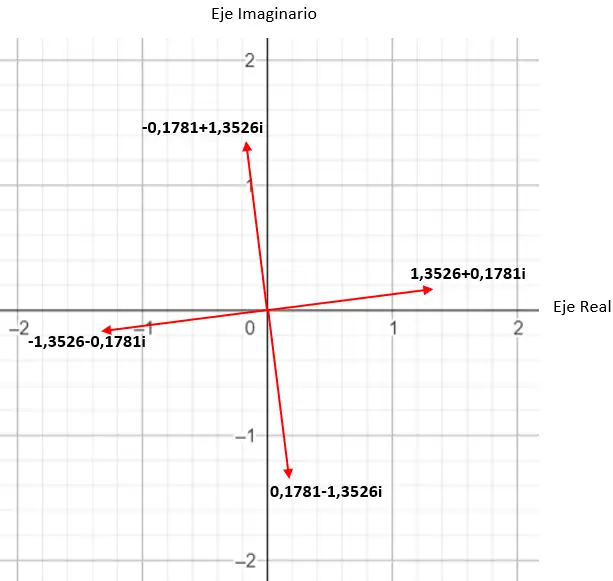
Örneğin bir kompleksin dördüncü kökünü hesaplarsak 4 farklı çözüm elde ederiz. Ve bunu karmaşık düzlemde ifade edersek, düzlemin orijini merkezli, 4 kenarı olan düzgün bir çokgenin oluştuğunu görürüz. Bu, daha sonra (örnekler bölümünde) ayrıntılı olarak göreceğimiz çok ilginç bir özelliktir.
Artık bu kavramı açıklığa kavuşturduğumuza göre, karmaşık bir sayının kökünün kutupsal biçimde nasıl hesaplanacağını göreceğiz (bir kökü çözmek için bu gösterimi kullanmak en rahat yöntemdir). Basitçe modülün kökünü hesaplamanız ve argümanı n cinsinden ifade etmeniz gerekir. Başka bir deyişle, aşağıdaki karmaşık sayının (z) kökü:
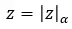
Hesaplanacak bu tutarlar:
- Modül: İlk modülün n’inci kökü.
- Bağımsız Değişken: Bağımsız değişkene radyan cinsinden 2πk veya derece cinsinden 360k ekleyin ve n’ye bölün.
Matematiksel olarak modülü ve argümanı hesaplamak için aşağıdaki iki formülü kullanırız:
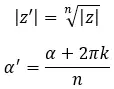
Burada, k = 0, 1, 2,…, n-1.
Dolayısıyla sonucu şu şekilde ifade ediyoruz:
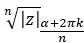
Açıkça söylemek gerekirse, bu kökü çözerek elde edeceğimiz n çözüm, aynı modül ve n farklı argümandan oluşacaktır.
Komplekslerin n’inci köklerini hesaplama örnekleri
Şimdi karmaşık sayıların n’inci köklerinin hesaplanmasına ilişkin bazı örnekler göreceğiz. Bunları kendi başınıza çözmeye çalışmanızı ve işiniz bittiğinde düzeltmeye bakmanızı öneririz. Yöntemin hemen yukarıda anlatıldığını unutmayın.
Karmaşık sayının üçüncü kökünü bulun: 1 + i √3 .
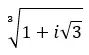
Karmaşık sayının dördüncü kökünü bulun: 3+i √ 3 .
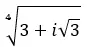
Karmaşık sayıların kökleri hakkında bilgi edinin
- Karışık sayılar
- Karmaşık sayılarla ilgili işlemler
- karmaşık güçler
- Karmaşık sayıların özellikleri