Karmaşık sayılar, gerçek sayılar ve sanal sayılardan oluşan bir kümedir. Bu son iki sayısal küme, gerçek çizgi ve sanal çizgi kullanılarak grafiksel olarak temsil edilebilir . Ve her iki doğruyu da aynı düzleme yerleştirdiğimizde, iyi bilinen karmaşık düzlem oluşur.
Karmaşık plan nedir?
Karmaşık düzlem, gerçek çizgiye eşdeğer olan gerçek eksen (X ekseni) ve diğer yandan sanal çizgiyi kavramsallaştıran sanal eksen (Y ekseni) tarafından oluşturulur.
Bu planın tüm karmaşık sayıları içerdiğini belirtmek gerekir. Dolayısıyla ne kadar küçük ya da küçük olursa olsun, karmaşık sayı hangi biçimde yazılırsa yazılsın plan üzerinde grafiksel olarak gösterilebilir. Şimdi bu sayıların karmaşık düzlemde nasıl temsil edildiğini görelim.
Karmaşık sayıların karmaşık düzlemde grafiği nasıl çizilir?
Zaten bildiğimiz gibi (ya da bilmiyorsanız karmaşık sayılar hakkındaki makalemizi okumanızı öneririz), bir kompleksi yazmanın üç yolu vardır: binom formu, kutupsal form ve trigonometrik form. Her biri karmaşık değeri farklı bir yapıya göre ifade eder, dolayısıyla grafik gösterimlerin yapılmasında izlenecek yöntem farklıdır.
Daha sonra, üç durumda izlenecek prosedürü açıklıyoruz:
Binom formunda temsil
En yaygın olanı olan binom gösteriminde karmaşık bir sayıya sahip olduğumuzda, sayının yapısına bakmamız gerekir:

burada a gerçek kısımdır ve b sanal kısımdır.
Bunu bilerek a’nın değerinin apsis için kullandığımız değer (gerçek eksen), b’nin değerinin de bilgisayar için kullandığımız değer (sanal eksen) olduğu sonucuna varırız. Aşağıdaki örnekle bunu daha iyi anlayacaksınız.
Sayıyı temsil etmeye çalışacağız: 3 + 2i.
İlk şey grafiği çizmektir (yatay eksenin gerçek, dikey eksenin sanal olduğunu unutmayın):

Daha sonra grafiğin noktasını karmaşık sayıdan çıkardığımız Kartezyen koordinatlarda (x, y) buluyoruz. Bu pratik örnekte, noktamız (3, 2)’dir.
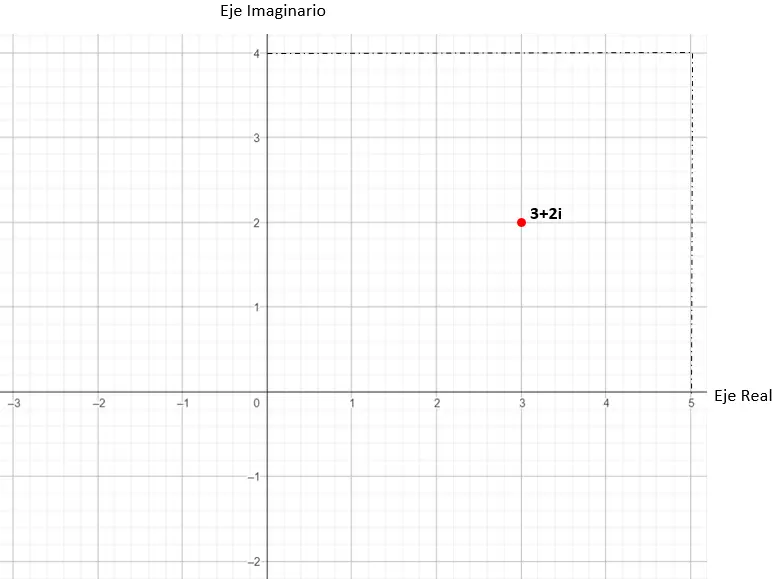
Böylece 3 + 2i değeri karmaşık düzlemde temsil edilecektir.
Kutupsal formda temsil
Şimdi karmaşık bir sayının kutupsal formda nasıl temsil edildiğini göreceğiz. Bu yöntemi tam olarak anlamak için kutupsal gösterimin modüle ve argümana dayalı bir karmaşık sayıyı tanımladığını bilmeniz gerekir. Grafiksel gösterimde kutupsal koordinatlar olarak kullanılırlar (Kartezyen koordinatlar olarak değil!).
Kutupsal koordinat sisteminin temel özelliği ise bir noktanın konumunun bir vektör ve bir açı aracılığıyla tanımlanmasıdır (önceki yöntemden farklı olarak). Bu, karmaşık sayıların modülüne ve argümanına karşılık gelir. Daha sonra size karmaşık bir sayının kutupsal formunun evrensel formülünü gösteriyoruz:

Nerede |z| modül ve α argümandır. Bu iki değişken planda şu şekilde çevrilir:
- Modül: Bir vektörü (başlangıç noktası ile sayımıza karşılık gelen nokta arasındaki) tanımlayan uzunluktur.
- Argüman: vektörün X ekseniyle yaptığı açıdır.
Bu nedenle karmaşık bir sayının modülü, grafiği oluşturmak için kullandığımız vektörün uzunluğuna karşılık gelir. Karmaşık sayının argümanı veya açısı, vektör ile X ekseni arasındaki açıdır. Aşağıda tüm değişkenlerin yerleştirildiği bir diyagramı görebilirsiniz:
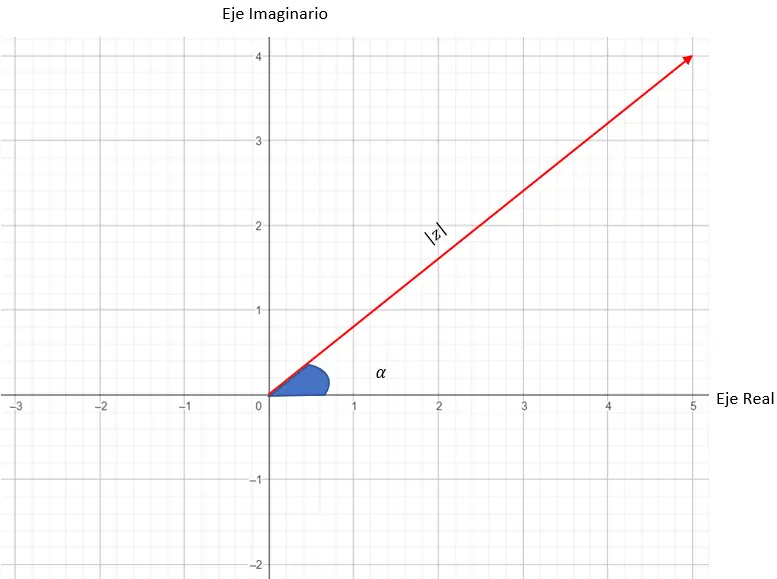
Şimdi şu sayıyı temsil etmeye çalışacağız: 3 45 .
Öncelikle modülü ve argümanı tanımlamamız gerekiyor:
- Modül: 3.
- Tartışma: 45 derece.
Daha sonra grafikte modülü 3’e eşit olan noktaları bulmamız gerekiyor, bu durumda yarıçapı 3 olan bir daire üzerindeki herhangi bir nokta işe yarayacaktır.
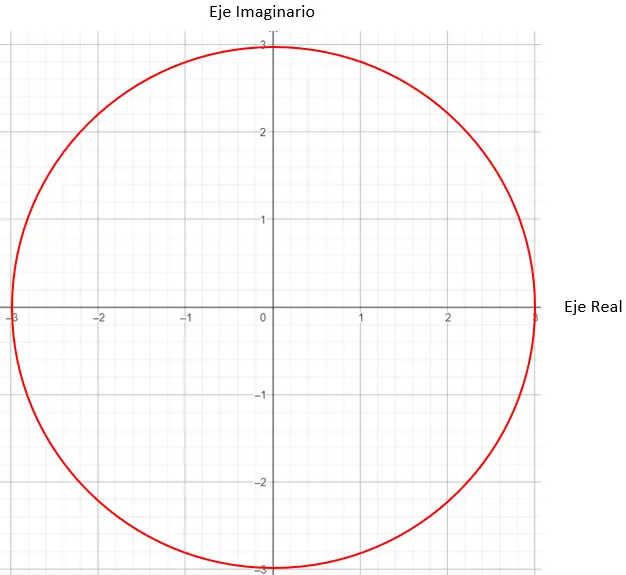
Ve kesin noktanın ne olduğunu belirlemeyi bitirmek için, modül tarafından oluşturulan vektörün ve orijinin X ekseniyle 45 derecelik bir açı yapması şartını koymalıyız.
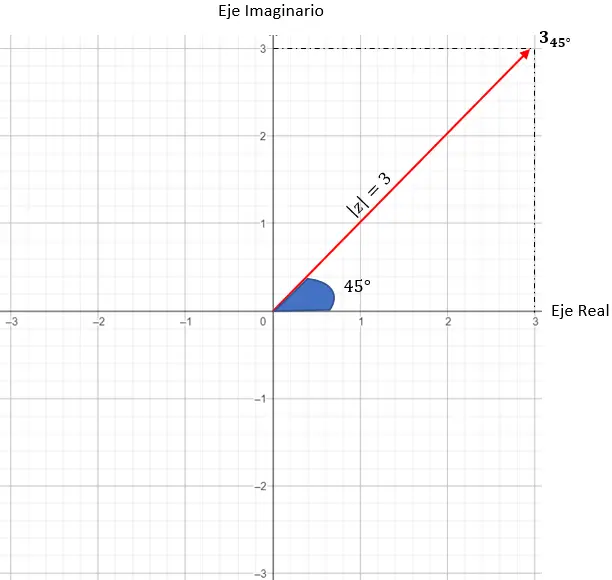
Ve zaten kutupsal gösterimle temsil edilen bir karmaşık sayıya sahibiz.
Trigonometrik formda gösterim
Son olarak, karmaşık bir sayının trigonometrik formda nasıl temsil edildiğini hala açıklamamız gerekiyor. Bu durum ve önceki durum hemen hemen aynıdır, çünkü kutupsal form ve trigonometrik form, karmaşık bir sayıyı ifade etmek için aynı verileri kullanır: modül ve argüman. Bu yalnızca ifadenin yapısını değiştirir:

Nerede, |z| modül ve α argümandır.
Bu nedenle, önceki durumda olduğu gibi aynı yöntemin avantajlarından yararlanmalıyız: modülü “uzunluk” olarak ve argümanı açı olarak kullanın. Aşağıdaki örneği görünce bunu daha iyi anlayacaksınız.
z = 4 · (cos (45) + i · sin(45)) ifadesini temsil edeceğiz.
İlk şey modülü ve açıyı tanımlamaktır:
- Modül: 4.
- Tartışma: 45 derece.
Daha sonra grafikte modülü 4’e eşit olan noktaları bulmamız gerekiyor, bu durumda yarıçapı 4 olan bir daire üzerindeki herhangi bir nokta işe yarayacaktır.
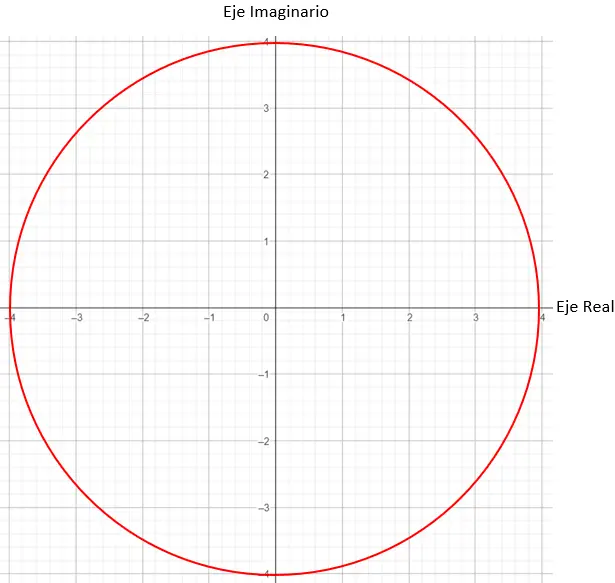
Ve son olarak, argümanın bize söylediği gibi, modül vektörü ile X ekseni arasında oluşan açının 45 derece olmasını gerektiren tam noktayı buluyoruz.
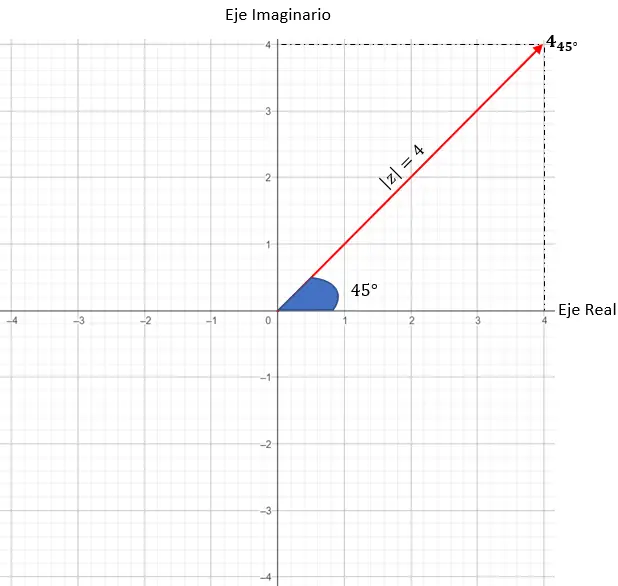
Ve böylece karmaşık bir sayıyı trigonometrik biçimde temsil ediyoruz.
Karmaşık uçak egzersizi
Bu yayını bitirmek için son bir alıştırma sunacağız. Bu sorunu çözmenizi şiddetle tavsiye ediyoruz, çünkü bu şekilde bu makale boyunca açıklanan bilgileri pekiştireceksiniz.
Aşağıdaki üç karmaşık sayının karmaşık düzlemde grafiksel gösteriminin kanıtı:
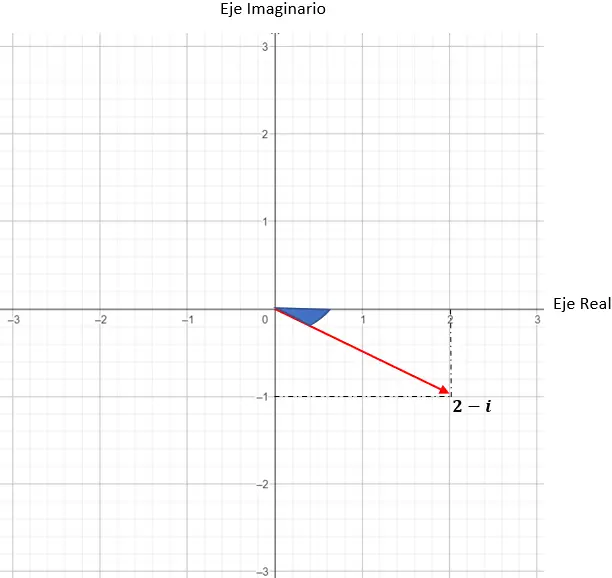
z = 2 – ben
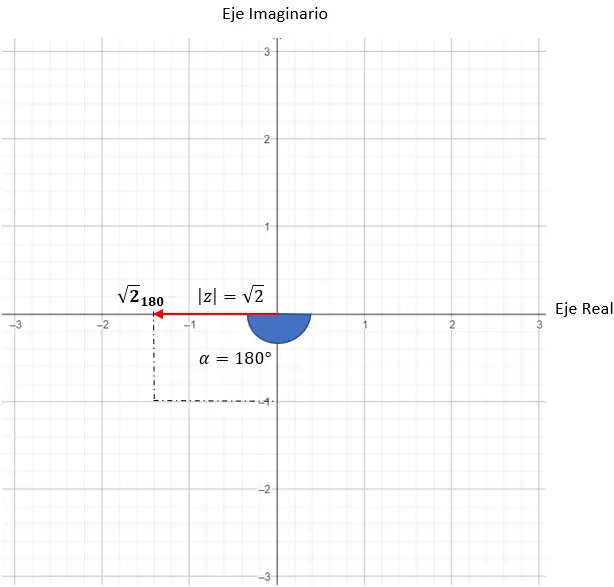
w = √2180
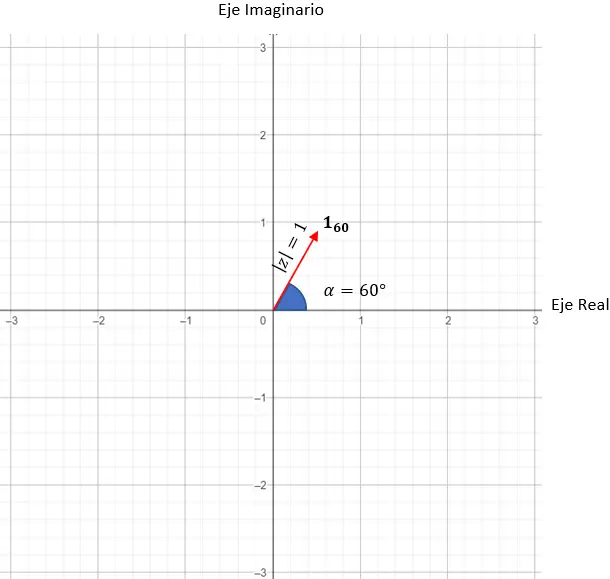
p = cos(60) + ben günah(60)
Karmaşık plan hakkında daha fazla bilgi edinin
- Karışık sayılar
- hayali sayılar