▷ Fonksiyonların bileşimi (veya bileşik fonksiyon)

Bu makalede bileşik fonksiyonun (veya fonksiyonların bileşiminin) ne olduğunu açıklıyoruz. Ek olarak, bileşik fonksiyonların birkaç örneğini ve bu tür fonksiyonların tanım alanlarının nasıl hesaplandığını görebileceksiniz. Son olarak, fonksiyon kompozisyonunun özelliklerini ve pratik yapabileceğiniz birkaç adım adım alıştırmayı bulacaksınız.

Fonksiyon bileşimi nedir?

Fonksiyon bileşimi, bağımsız değişkenin (x) aynı değerinin iki veya daha fazla fonksiyonda art arda değerlendirilmesinden oluşur. Örneğin, (gof)(x) fonksiyonlarının birleştirilmesi, g[f(x)] bileşik fonksiyonunu verir.

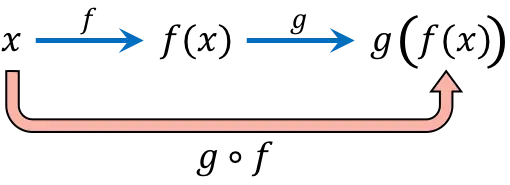
Bileşik fonksiyonun ifadesi

$g\circ f$

“f’nin g ile birleşimi” veya “f’nin ardından g” okuruz.

İşlev bileşiminde sıranın önemli olduğunu unutmayın; bileşim sembolünün sağındaki işlev ilk olarak uygulanır

$(f)$

ardından kompozisyon sembolünün solundaki işlev

$(g).$

Fonksiyon bileşimi örneği

Bileşik fonksiyonun tanımı göz önüne alındığında, iki fonksiyonun bileşiminin nasıl hesaplanacağına dair bir örnek görelim.

Aşağıdaki iki farklı fonksiyon göz önüne alındığında:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Bileşik fonksiyonunu hesaplayın

$\left(g \circ f\right)(x)$

ve bunu değerlendirin

$x=3.$

Fonksiyonların bileşimi

$\left(g \circ f\right)(x)$

Bu, aşağıdaki bileşik işlevi gerçekleştirmemiz gerektiği anlamına gelir:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Bunu çözmek için değiştiriyoruz

$f(x)$

cebirsel ifadesiyle:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

Ve şimdi fonksiyonunu alıyoruz

$g(x)=\cfrac{x+4}{2}$

ve ifadeyi koyuyoruz

$3x+1$

nerede bir tane var

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

Bu şekilde, g’den oluşan f fonksiyonunu zaten hesaplamıştık:

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Son olarak bileşik fonksiyonu değerlendirmek için

$x=3$

Basitçe fonksiyonun görüntüsünü söz konusu değerde hesaplayın:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Bileşik işlev alanı

Normalde, fonksiyonlar üzerinde işlemler yaptığımızda, ortaya çıkan fonksiyonun tanım kümesi, orijinal işlevlerin tanım kümelerinin kesişimidir. Ancak bu özellik fonksiyon bileşimi tarafından karşılanmamaktadır.

Fonksiyon kompozisyonunun alanı

$(g\circ f)(x)$

fonksiyonun tanım kümesindeki x’in tüm değerlerinin kümesine eşdeğerdir

$f$

örneğin

$f(x)$

fonksiyon alanına aittir

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Bu nedenle, bir bileşik fonksiyonun tanım kümesini hesaplamak için, önce her bir işlevin tanım kümesini ayrı ayrı bulmanız, ardından işlem sonucu ortaya çıkan işlevin tanım kümesini bulmanız gerekir. Böylece fonksiyonların bileşim alanı, önceki matematiksel koşulu karşılayan tüm değerlerden oluşacaktır.

👉Unutmayın, nasıl çözeceğinizi bilmediğiniz bir sorunla karşılaşırsanız aşağıdaki yorumlardan bize sorabilirsiniz!

Fonksiyon kompozisyonunun özellikleri

Bileşik işlevler aşağıdaki özelliklere sahiptir:

Fonksiyonların bileşimi ilişkisel özelliğe sahiptir, bu nedenle aşağıdaki denklem her zaman doğrudur:

$f\circ (g\circ h)=(f\circ g)\circ h$

Genel olarak fonksiyon bileşimi değişmeli değildir, dolayısıyla işlemin sırası sonucu belirler:

$f\circ g\neq g\circ f$

Fonksiyonların bileşiminin nötr elemanı kimlik fonksiyonuna karşılık gelir
$f(x)=x.$

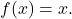
Böylece, kimlik işleviyle oluşturulan herhangi bir işlev, işlevin kendisiyle sonuçlanır:

$f\circ id = id \circ f = f$

$id = x$

İki fonksiyonun bileşkesinin tersini hesaplamak, önce her bir fonksiyonun tersini bulmaya, sonra da bileşik fonksiyonu bulmaya eşdeğerdir:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Ters fonksiyon aynı zamanda bileşik fonksiyonun simetrik bir elemanı olarak da hareket eder, çünkü bir fonksiyonun tersiyle bileşimi özdeş fonksiyona eşdeğerdir:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

İki fonksiyonun bileşiminin türevi zincir kuralı kullanılarak hesaplanır:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Bakınız: zincir kuralı nedir?

Fonksiyonların bileşimi ile ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki iki fonksiyon göz önüne alındığında:

$f(x)=x-2 \qquad g(x)= 5x + 4$

g ile birleştirilmiş f ve f ile birleştirilmiş g fonksiyonlarının bileşimlerini hesaplayın.

$(g\circ f)(x)$

$(f\circ g)(x)$

Çözümü görün

Fonksiyonların bileşimi

$\left(g \circ f\right)(x)$

aşağıdaki bileşik fonksiyonu hesaplamak anlamına gelir:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Yani çözmek için değiştiriyoruz

$f(x)$

ifadesi için:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$

Bu şu anlama gelir: ifadesinde

$g(x) =5x+4$

değişkeni değiştirmeniz gerekir

$x$

İçin

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Henüz:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Öte yandan, f’den oluşan g fonksiyonunu bulmak için aynı işlemi ters sırayla yapmanız gerekir:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Bu alıştırma aynı zamanda bileşik fonksiyonların değişmeli olmadığı özelliğini de gösterir, çünkü sonuç, fonksiyonların uygulanma sırasına bağlıdır.

Alıştırma 2

Aşağıdaki iki fonksiyon göz önüne alındığında:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

g ile oluşan f fonksiyonlarının bileşimini hesaplar.

$(g\circ f)(x)$

Çözümü görün

g’den oluşan f fonksiyonu, aşağıdaki bileşik fonksiyonun çözülmesi anlamına gelir:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Bu nedenle f(x) fonksiyonunu onun ifadesiyle değiştiririz:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

Ve şimdi değiştirmeliyiz

$x$

İçin

$x^2-3$

g(x) fonksiyonunun ifadesinde:

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

Kısaca fonksiyon bileşiminin sonucu:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Alıştırma 3

Aşağıdaki iki ikinci dereceden fonksiyon göz önüne alındığında:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Aşağıdaki fonksiyon bileşiminin sonucunu belirleyin:

$(g\circ f)(2)$

Çözümü görün

$\left(g \circ f\right)(2)$

aşağıdaki bileşik fonksiyonun bulunmasından oluşur:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Bileşik fonksiyonu çözmek için önce hesaplıyoruz

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Bu nedenle,

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Bileşik fonksiyonun değerini bulmak için hesaplamanız yeterlidir.

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

Özetle, fonksiyon kompozisyonu probleminin sonucu şudur:

$\bm{\left(g \circ f\right)(2) =8}$

Alıştırma 4

Aşağıdaki iki fonksiyon göz önüne alındığında:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

x=2’de f ile oluşturulan g’nin sonucunu bulun:

$(f\circ g)(2)$

Çözümü görün

Bu durumda aşağıdaki bileşik fonksiyonu hesaplamamız gerekir:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

O halde ilk önce buluyoruz

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

Ve böylece

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Bileşik fonksiyonu çözmek için hesaplamamız gerekir

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$