Bu yazımızda fonksiyonlarla hangi işlemlerin yapılabileceğini açıklıyoruz. Fonksiyonlu işlemlerle ilgili açıklamaların yanı sıra çözülmüş alıştırmaları da görebileceksiniz. Ve son olarak, fonksiyonlarla birlikte işlemlerin özelliklerini bulacaksınız.
Fonksiyonlu işlemler nelerdir?
Toplama, çıkarma, çarpım, bölme ve kompozisyon olmak üzere 5 farklı işlem türünü işlevlerle gerçekleştirebilirsiniz. Yani iki fonksiyon toplanabilir, çıkarılabilir, çarpılabilir, bölünebilir veya birleştirilebilir.
Daha sonra, her bir operasyon türünün nasıl yürütüldüğünü, her birinin işlevleri ve özellikleriyle birlikte göreceğiz.
Fonksiyonların toplamı
İki fonksiyonun toplamının (veya toplamının) değeri, her fonksiyonun değerinin toplamına eşittir. Başka bir deyişle, bir toplam fonksiyonunun görüntüsünü hesaplamak için, işlemde yer alan fonksiyonların görüntülerini eklemeniz yeterlidir.
![]()
Ayrıca, iki fonksiyonun toplamının alanı, her bir toplam fonksiyonun alanının kesişimidir.
![]()
Bir örnek kullanarak iki fonksiyonun nasıl eklendiğini görelim:
![]()
İlk önce iki işlevi ekliyoruz:
![]()
Şimdi toplam fonksiyonunun tanım kümesini buluyoruz. Bunu yapmak için her fonksiyonun tanım kümesini ayrı ayrı hesaplıyoruz:
![]()
➤ Bakınız: bir fonksiyonun tanım kümesi nasıl hesaplanır
O zaman işlem sonucunda ortaya çıkan fonksiyonun tanım kümesi şu şekilde olacaktır:
![]()
Sonucu tam olarak tanımlayabilmek için, işlevlere sahip her bir işleme kendi etki alanı eşlik etmelidir.
Fonksiyonların çıkarılması
İki fonksiyonun çıkarılmasının (veya farkının) görüntüsü, işleme katılan her fonksiyonun görüntülerinin çıkarılmasıdır:
![]()
Toplama fonksiyonunda olduğu gibi, iki fonksiyonun çıkarma tanım kümesi, her bir işlevin tanım kümesinin kesişimine eşdeğerdir.
![]()
Yani bağımsız x değişkeninin belirli bir değerinde bir fonksiyon tanımlanmamışsa, çıkarma sonucu ortaya çıkan fonksiyon da tanımlanmayacaktır.
Bir örnek üzerinden iki fonksiyonun nasıl çıkarıldığını görelim:
![]()
Önce iki fonksiyonu çıkarıyoruz:
![]()
Daha sonra çıkarma fonksiyonunun tanım kümesini belirleriz:
![]()
![]()
Amiral gemisi ürünü
İki fonksiyonun çarpımını veya (çarpmasını) hesaplamak için her fonksiyonun ifadesini çarpmanız yeterlidir.
![]()
Öte yandan, çarpım fonksiyonunun alanı, her çarpılmış fonksiyonun alanının kesişimlerinin kümesidir.
![]()
Örneğin, aşağıdaki iki fonksiyona sahipsek:
![]()
Öncelikle ürünün çalışmasını iki fonksiyonla gerçekleştiriyoruz:
![]()
Ve son olarak, işlemin sonucunda ortaya çıkan fonksiyonun tanım kümesini buluyoruz:
![]()
![]()
Fonksiyonların dağılımı
İki fonksiyonun bölünmesinin (veya bölümünün) sayısal sonucu aşağıdaki denkleme karşılık gelir:
![]()
Bununla birlikte, iki fonksiyonun bölme bölgesi, her fonksiyonun alanının kesişim kümesinden, bölen olarak görev yapan fonksiyonu iptal eden tüm x’lerin çıkarılmasıyla elde edilir, çünkü aksi takdirde bir belirsizlik elde ederiz.
![]()
Örnek olarak aşağıdaki işlevleri böleceğiz:
![]()
Fonksiyonların dağılımı aşağıdaki gibidir:
![]()
Öte yandan, her fonksiyonun tanım kümesi ayrı ayrı tüm gerçek sayılardan oluşur.
![]()
Ancak bir kesrin paydasında sıfır olamayacağından, elde edilen fonksiyonun tanım kümesinde paydayı (x=3) sıfırlayan tüm değerleri çıkarmamız gerekir.
![]()
Fonksiyonların bileşimi
Fonksiyonların bileşkesi çözülmesi en zor işlemdir çünkü en karmaşık kavramdır.
Fonksiyon bileşimi iki fonksiyonun ardışık uygulanmasından oluşur. Cebirsel olarak iki fonksiyonun bileşimi şu şekilde ifade edilir:
![]()
Öte yandan, fonksiyonların bileşkesi alanı
![]()
fonksiyonun tanım kümesindeki x’in tüm değerlerinin kümesine eşdeğerdir
![]()
örneğin
![]()
fonksiyon alanına aittir
![]()
![]()
Örneğin, aşağıdaki iki işlev verildiğinde:
![]()
Bileşik fonksiyonu bulmak için
![]()
bunu takiben
![]()
ifadesini değiştirmemiz gerekiyor
![]()
nerede bir tane var
![]()
ifadesinde
![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
Bu durumda her iki fonksiyonun tanım kümesi tamamen reel sayılardan oluştuğu için bileşik fonksiyonun tanım kümesi de reel sayılardan oluşacaktır.
![]()
Gördüğünüz gibi fonksiyonların oluşturulması anlaşılması kolay bir işlem değildir. Bu nedenle aşağıdaki fonksiyon kompozisyonu alıştırmalarını yapmanızı öneririz:
➤ Bakınız: fonksiyonların bileşimi ile ilgili çözümlü alıştırmalar
Fonksiyonlu işlemlerin özellikleri
Fonksiyonlu tüm işlemlerin toplamı ve çarpımı aşağıdaki özelliklerle karakterize edilir:
- İlişkisel özellik : 3 veya daha fazla fonksiyonun eklenme veya çarpılma sırası önemsizdir.
![]()
![]()
- Değişme özelliği : İki fonksiyonun toplama veya çarpma sırası sonucu değiştirmez.
![]()
![]()
- Nötr eleman: toplam işlemi ve çarpım işlemi sabit nötr eleman fonksiyonlarına sahiptir
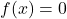
Ve
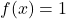
sırasıyla.
- Simetrik eleman : toplam fonksiyonunun zıt fonksiyonu vardır
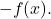
- Dağılma özelliği : Bu özellik, işlemlerin toplamını ve çarpımını birbirine bağlar ve aşağıdaki eşitliğe dayanır:
![]()