Bu sayfada fonksiyon dönüşümlerinin ne olduğu ve bunların nasıl bulunacağı açıklanmaktadır. Üç tür dönüşüm vardır: ötelemeler (veya yer değiştirmeler), simetriler ve genişlemeler (veya daralmalar). Ayrıca adım adım çözülmüş alıştırmalar da bulacaksınız, böylece hiçbir şüpheye yer bırakmadan pratik yapabilir ve kavramları anlayabilirsiniz.
Fonksiyon dönüşümleri nelerdir?
Bazen bizden zaten bildiğimiz diğerlerine çok benzeyen temel fonksiyonların grafiğini çizmemiz istenebilir. Benzer işlevi tekrar temsil etmek yerine, bir işlevi temsil etmekten diğerine kolay ve hızlı bir şekilde geçiş yapmak için teknikler kullanılabilir.
Dolayısıyla fonksiyon dönüşümleri , temel işlemler yoluyla bir fonksiyonun grafiksel gösteriminden çok benzer başka bir fonksiyonun grafiksel gösterimine geçmeyi mümkün kılan tekniklerdir.
Temel olarak, temel fonksiyonların üç tür dönüşümü vardır:
- Çeviriler veya hareketler : Bir işlev dikey ve yatay olarak hareket ettirilebilir.
- Yansımalar veya simetriler : Bir fonksiyon, simetri ekseni olarak X ekseni veya Y ekseni kullanılarak yansıtılabilir.
- Genişletmeler ve sıkıştırmalar : Bir işlev büyütülebilir veya küçültülebilir.
Bir işlevi dönüştürme kavramını gördükten sonra, her değişiklik türünü daha derinlemesine inceleyeceğiz.
İşlevlerin çevirileri veya hareketleri
Fonksiyon değişimleriyle başlayacağız. İki tür vardır: dikey çeviriler ve yatay çeviriler.
Bir fonksiyonun ötelenmesi veya dikey hareketi
Bir işlevi dikey olarak (Y ekseni boyunca) çevirmek veya taşımak için, işleve bir sabit eklemeniz veya çıkarmanız gerekir:
Bir fonksiyonu k birim yukarıya, fonksiyona ka ekleyerek taşırız:
![]()
Bir fonksiyonu k birim aşağı kaydırmak için ka’yı fonksiyondan çıkarırız:
![]()
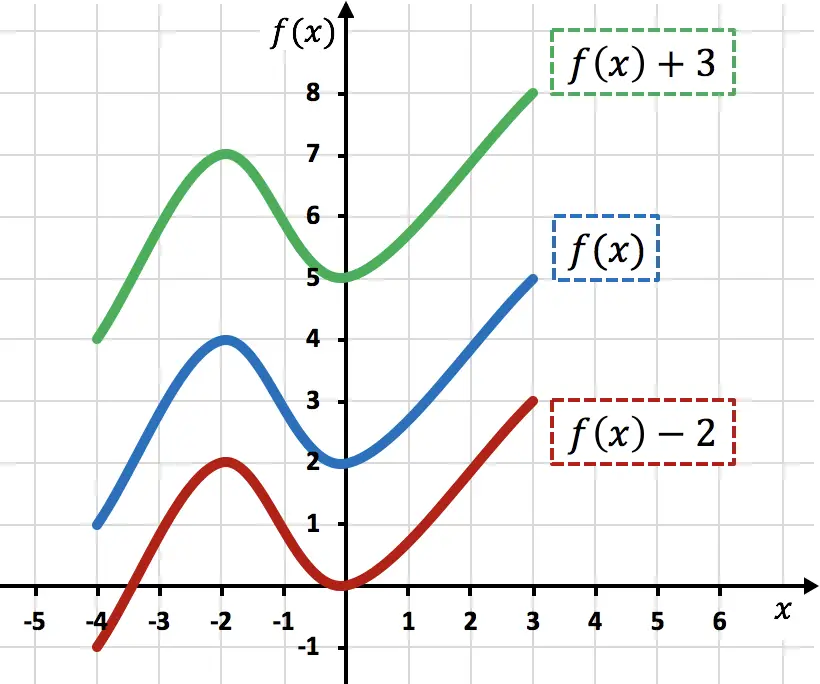
Grafikten de görebileceğiniz gibi, herhangi bir fonksiyona bir sabit eklemek, eklenen birimleri yukarı kaydırır (yeşil fonksiyon). Öte yandan bir fonksiyondan sayı çıkarırken çıkarılan birimler aşağı doğru kaydırılır (kırmızı fonksiyon).
Bu tür hareketlerde fonksiyon noktalarının yalnızca Y koordinatlarının değiştiğini, X koordinatlarının aynı kaldığını unutmayın.
Fonksiyonların ötelenmesi veya yatay hareketi
Bir fonksiyonu yatay olarak (X ekseni boyunca) çevirmek veya kaydırmak için bağımsız x değişkenine bir sabit eklemeniz veya çıkarmanız gerekir:
Grafiği
![]()
grafiği
![]()
k birim sola kaydırıldı.
Grafiği
![]()
grafiği
![]()
k birim sağa kaydırıldı.
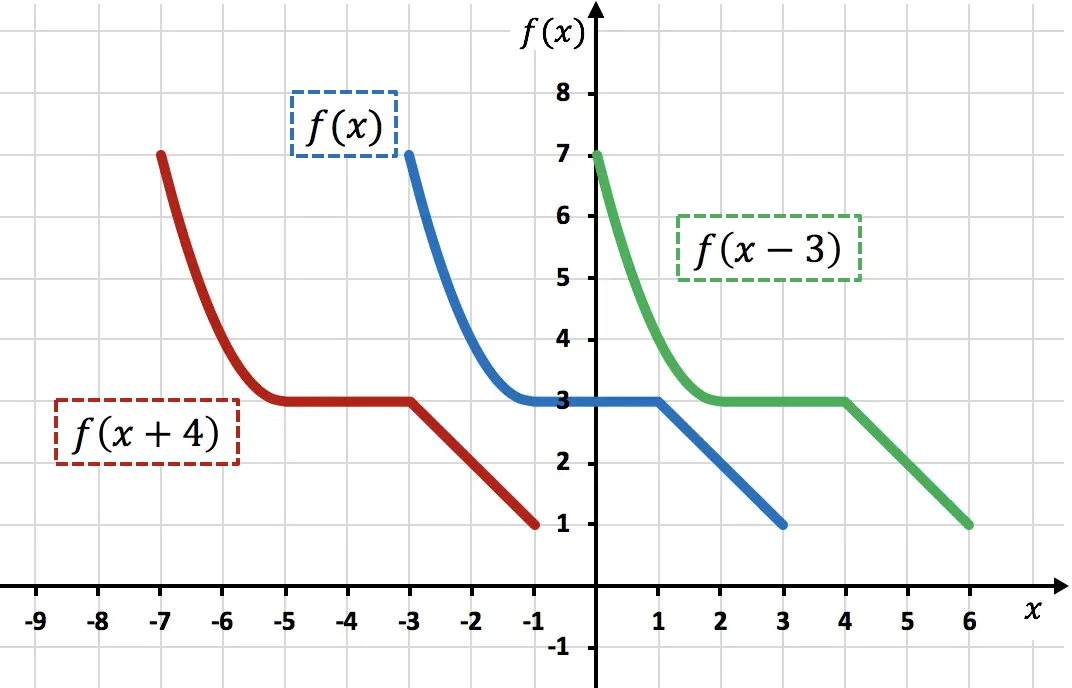
Grafikten de görebileceğiniz gibi x değişkenine doğrudan bir sabit eklerken fonksiyon eklenen birimleri sola kaydırır (kırmızı fonksiyon). Öte yandan, x değişkeninden bir sayı çıkarıldığında fonksiyon, çıkarılan birimleri sağa kaydırır (yeşil fonksiyon).
Bu tür hareketlerde fonksiyon noktalarının sadece X koordinatlarının değiştiğini, Y koordinatlarının ise aynı değerde devam ettiğini unutmayın.
Bir işlevi çevirme veya taşıma örneği
- Aşağıdaki fonksiyonu 4 birim yukarı ve 3 birim sağa taşıyın:
![]()
Fonksiyonu 4 birim yukarı taşımak için fonksiyona 4 birim eklememiz gerekir:
![]()
Ayrıca fonksiyonu 3 birim sağa kaydırmak için şunu hesaplamamız gerekir:
![]()
. Bu nedenle, nerede bir
![]()
yapabiliriz
![]()
![]()
Fonksiyon 4 birim yukarı ve 3 birim sağa kaydırıldığında şu şekilde olur:
![]()
Aşağıda orijinal fonksiyon ve dönüştürülmüş fonksiyonun grafiği verilmiştir, böylece aralarındaki farkı görebilirsiniz:
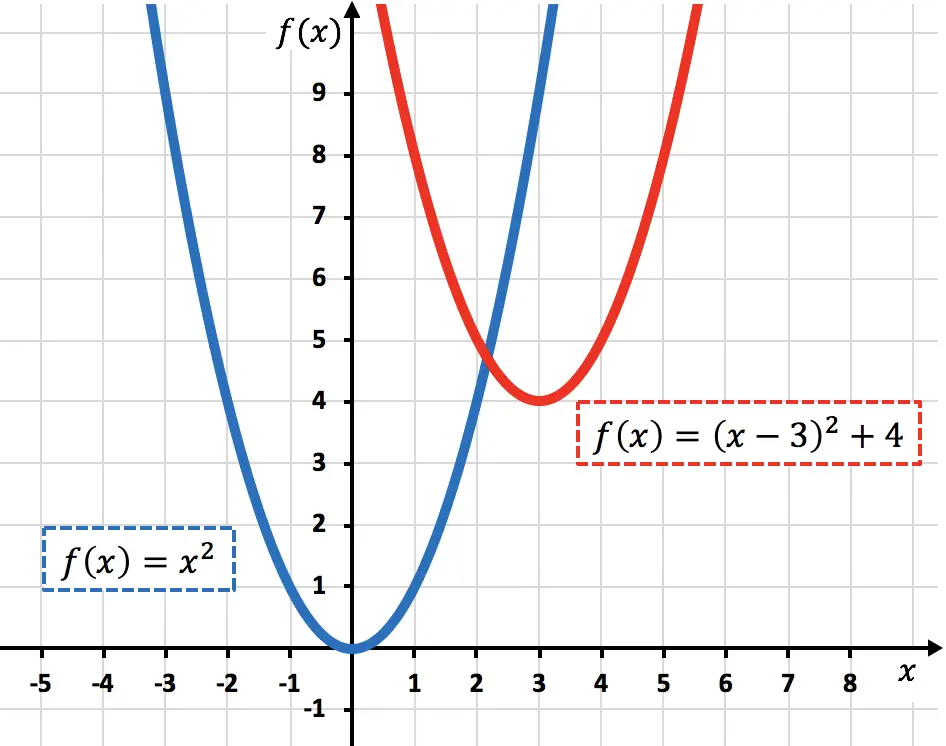
Bazı matematikçiler her iki hareket türü aynı anda meydana geldiğinde eğik yer değiştirme veya öteleme adını verirler.
Bir fonksiyonun koordinat eksenlerine göre yansıması veya simetrisi
Herhangi bir Kartezyen eksene göre simetrik fonksiyonu aşağıdaki şekilde temsil edebiliriz:
Bir fonksiyonu x eksenine göre yansıtmak için fonksiyonun işaretini değiştirmemiz gerekir, yani hesaplamamız gerekir.
![]()
Bir fonksiyonu y eksenine göre yansıtmak için bağımsız değişken x’i olumsuzlamamız gerekir, yani hesaplamamız gerekir
![]()

Önceki grafikte gördüğünüz gibi bir fonksiyonu -1 ile çarparak grafiksel olarak ters çevirmiş oluyoruz (turuncu fonksiyon), yani X eksenine göre aynalamış oluyoruz.
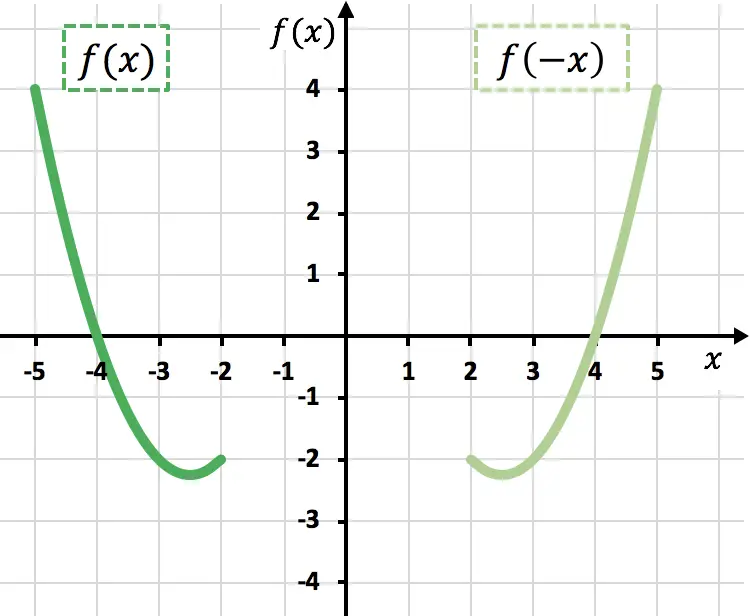
Önceki grafikte görülebileceği gibi x değişkenini olumsuzlayarak fonksiyonu Y eksenine göre yansıtıyoruz (açık yeşil fonksiyon).
Bir işlevi yansıtma örneği
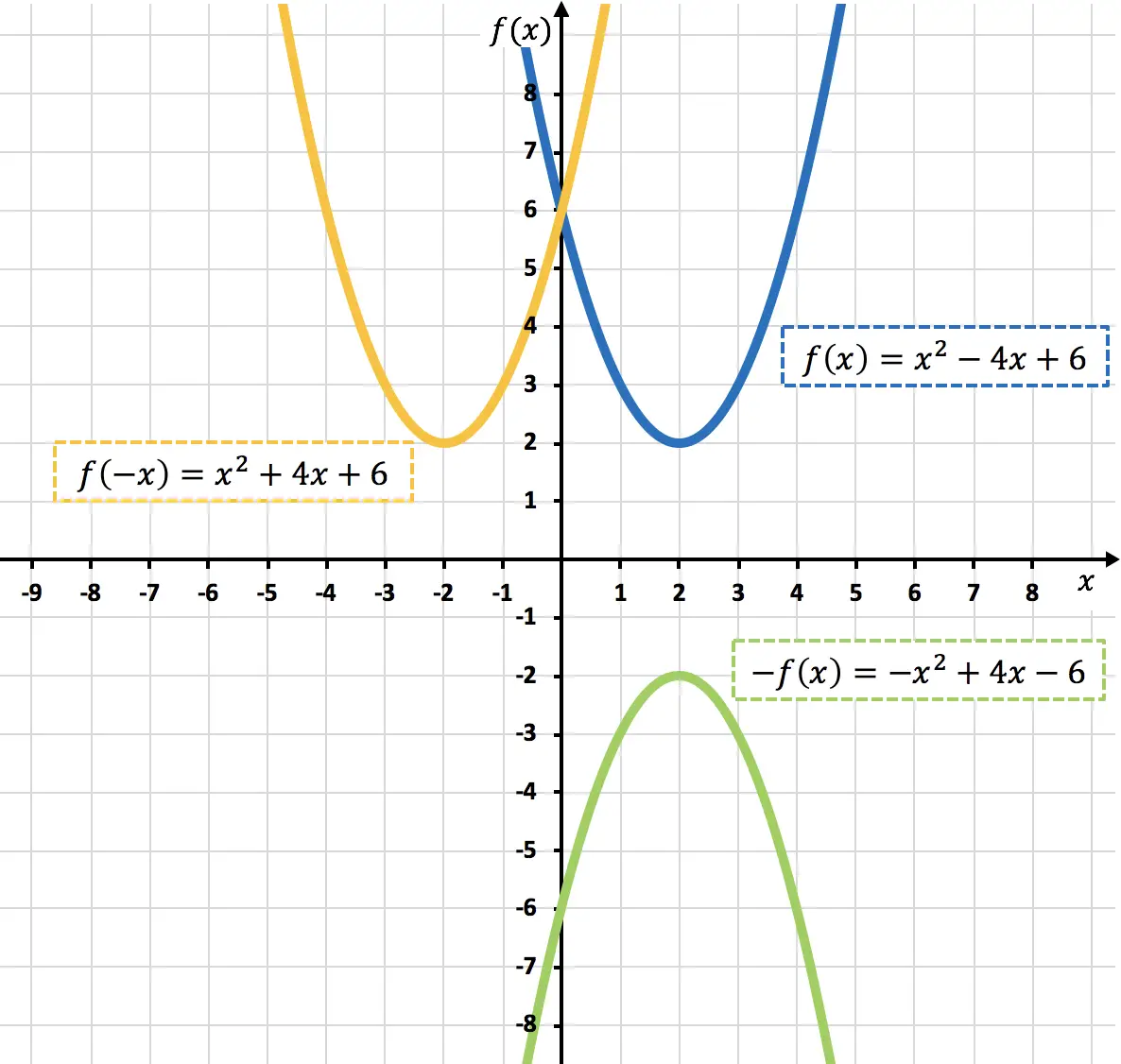
- Aşağıdaki ikinci dereceden fonksiyonun OX eksenine göre simetrik fonksiyonunu ve OY eksenine göre simetrik fonksiyonunu hesaplayın:
![]()
Fonksiyonu X eksenine göre simetrik bulmak için şunu yapmalıyız:
![]()
:
![]()
![]()
Fonksiyonu Y eksenine göre simetrik bulmak için şunu yapmalıyız:
![]()
. Bu nedenle, olduğu yeri değiştiririz.
![]()
terime göre orijinal fonksiyonda
![]()
![]()
![]()
![]()
![]()
Aşağıda hem orijinal fonksiyonu hem de bulunan simetrik fonksiyonları temsil ettiniz:
Fonksiyon genişlemeleri ve daralmaları
Çevirilerde olduğu gibi iki tür genişleme veya daralma vardır: dikey ve yatay.
Bir fonksiyonun dikey genişlemesi ve daralması
Bir tamsayı fonksiyonunu bir katsayı ile çarparak onun genişlemesini veya daralmasını sağlayabiliriz:
Bir fonksiyonu Y ekseninde genişletmek (veya genişletmek) için onu 1’den büyük bir sayıyla çarpmamız gerekir:
 Y eksenindeki bir fonksiyonu azaltmak için onu 1’den küçük pozitif bir sayıyla çarpmamız gerekir:
Y eksenindeki bir fonksiyonu azaltmak için onu 1’den küçük pozitif bir sayıyla çarpmamız gerekir:
 X eksenindeki bir fonksiyonu azaltmak için tüm x’leri 1’den büyük bir sayıyla çarpmamız gerekir:
X eksenindeki bir fonksiyonu azaltmak için tüm x’leri 1’den büyük bir sayıyla çarpmamız gerekir:

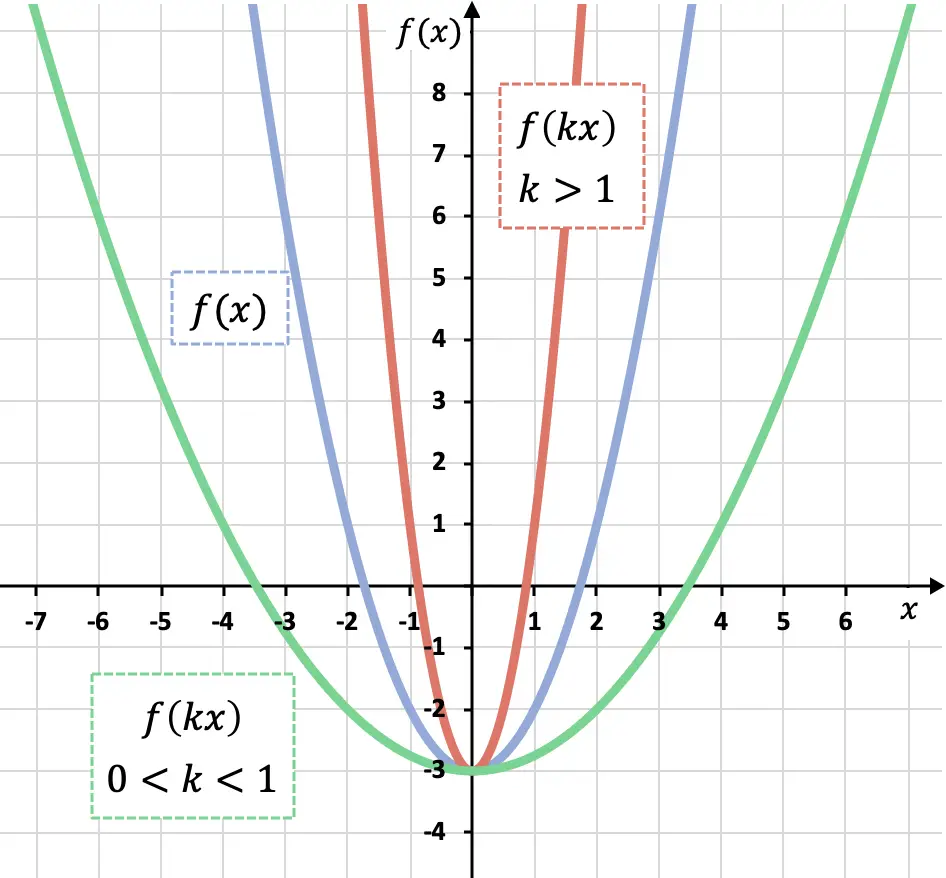
Önceki grafikte de görebileceğiniz gibi, bir fonksiyonun tüm x’lerini 0’dan büyük ancak 1’den küçük bir katsayı (yeşil fonksiyon) ile çarparsak, onu OX ekseni boyunca büyütürüz; 1’den büyük bir katsayıya sahip bir fonksiyon (kırmızı fonksiyon), onu OX ekseni boyunca azaltırız.
Bir işlevin nasıl genişletileceğine veya daraltılacağına ilişkin örnek
- Aşağıdaki irrasyonel fonksiyonu dikey ve yatay olarak kopyalayın:
![]()
Fonksiyonu y ekseninde iki katına çıkarmak için fonksiyonun tamamını 2 ile çarpmamız gerekir:
![]()
Ayrıca fonksiyonu x ekseninde iki kat genişletmek için fonksiyonun tüm x’lerini şununla çarpmamız gerekir:
![]()
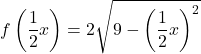
Dolayısıyla iki koordinat ekseninde kopyalanan fonksiyon şu şekildedir:
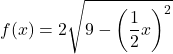
Aşağıda orijinal fonksiyon ve dönüştürülmüş fonksiyon grafiksel olarak gösterilmiştir, böylece aralarındaki farkları görebilirsiniz:
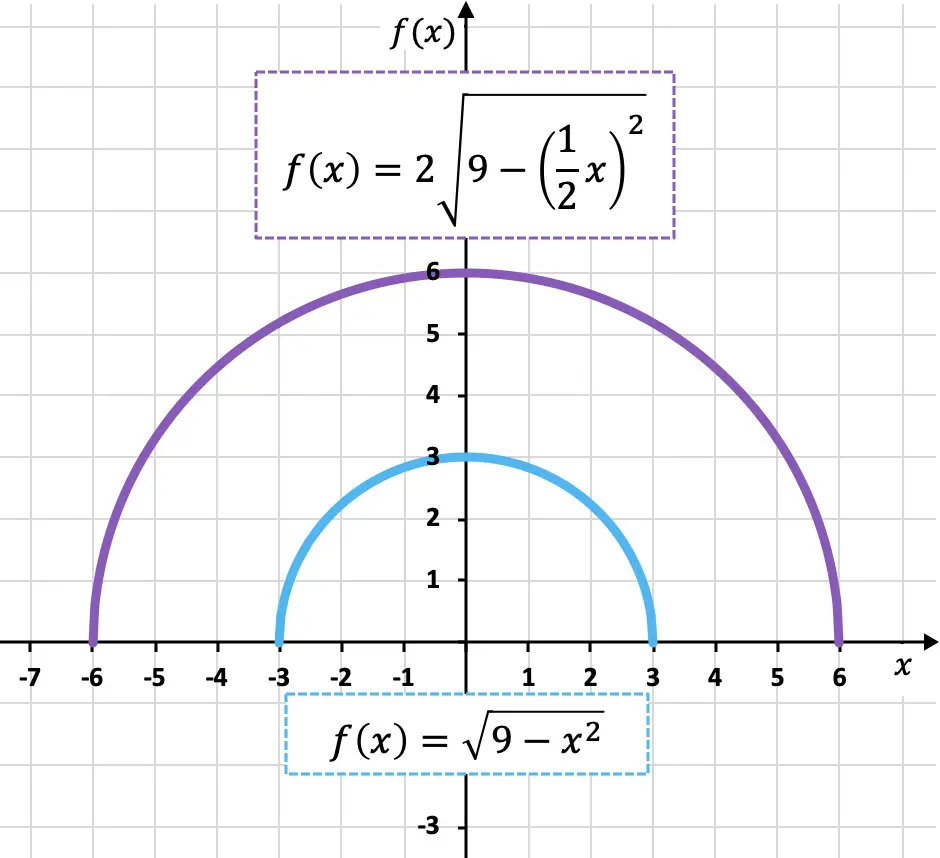
Gördüğünüz gibi yeni özellik (mor renk), orijinal özelliğe (mavi renk) göre hem dikey hem de yatay olarak iki kat daha büyük olduğundan özellik genişletilmiştir.
Fonksiyon dönüşümleri ile ilgili çözülmüş alıştırmalar
1. Egzersiz
Aşağıdaki üçüncü derece fonksiyonu 5 birim yukarı taşıyın:
![]()
Fonksiyonu 5 birim yukarı taşımak için fonksiyona 5 ekleyin:
![Rendered by QuickLaTeX.com \begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d29d1537293d975f7fbda8871622660f_l3.png)
Dolayısıyla 5 birim kaydırılan fonksiyon şu şekildedir:
![]()
Alıştırma 2
Aşağıdaki ikinci dereceden fonksiyonun Y eksenine göre simetrik fonksiyonunu bulun:
![]()
Fonksiyonu Y eksenine göre simetrik bulmak için hesaplamak gerekir
![]()
yani değiştirmemiz gerekiyor
![]()
İçin
![]()
fonksiyonda:
![]()
![]()
Dolayısıyla OY eksenine göre simetrik fonksiyon şu şekildedir:
![]()
Alıştırma 3
Aşağıdaki işlevi temsilinin üçte birine yatay olarak sıkıştırın:
![]()
Bir işlevi azaltmak için
![]()
![]()
![]()
Dolayısıyla indirgenmiş fonksiyon şu şekildedir:
![]()
Alıştırma 4
4 birim sağa çevrilmiş aşağıdaki fonksiyonun OX eksenine göre simetrik fonksiyonunu hesaplayın:
![]()
Simetrik fonksiyonu hesaplamadan önce fonksiyonu 4 birim sağa kaydırmalıyız, dolayısıyla:
![]()
![]()
![]()
Fonksiyonu hareket ettirdikten sonra X eksenine göre simetrik fonksiyonu hesaplıyoruz. Bunu yapmak için elde edilen fonksiyonu olumsuzlamamız gerekir:
![]()
![]()
Kısacası, tüm temel işlemleri uyguladıktan sonraki fonksiyon şöyledir:
![]()
Alıştırma 5
Aşağıdaki fonksiyonu 2 birim sola kaydırın, ardından dikey olarak 4 kat genişletin:
![]()
İlk önce fonksiyonu iki birim sola kaydırıyoruz:
![]()
![]()
![]()
Daha sonra fonksiyonu Y ekseni boyunca 4 faktörüyle genişletiyoruz:
![]()
![]()
Sonuç olarak, tüm temel dönüşümlerin uygulanmasından sonraki fonksiyon şöyledir:
![]()
Alıştırma 6
İşlevden
![]()
grafikteki gösterimlerden hangisinin fonksiyona karşılık geldiğini belirleyin
![]()
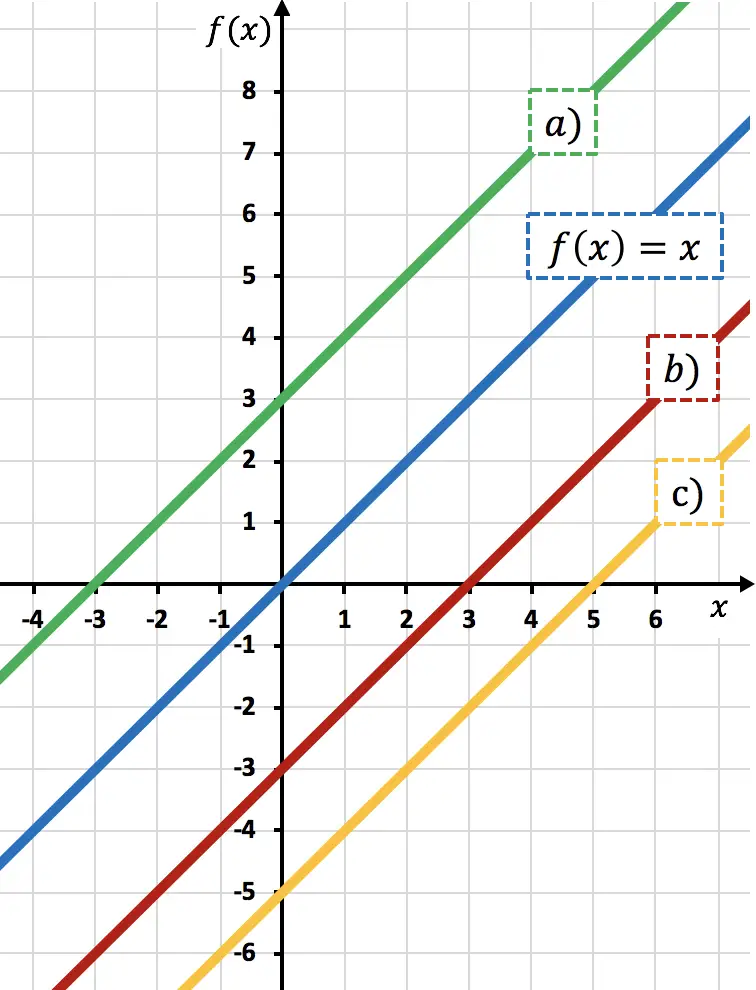
İşlev
![]()
fonksiyon
![]()
3 birim aşağıya doğru ilerledi. Çünkü bir fonksiyondan sayı çıkardığınızda fonksiyonu aşağıya doğru kaydırırsınız.
Bu nedenle temsili
![]()
b) çizgisine karşılık gelir, çünkü buna kıyasla 3 birim aşağıya doğru kaydırılmıştır.
![]()
Bu, dikey eksene bakarak görülebilir: ne zaman
![]()
0’dan geçiyor, kırmızı çizgi -3’ten geçiyor, yani 3 birim aşağı kaydırılıyor.
Egzersiz 7
İşlevden
![]()
hangi parabolün fonksiyonu temsil ettiğini belirleyin
![]()
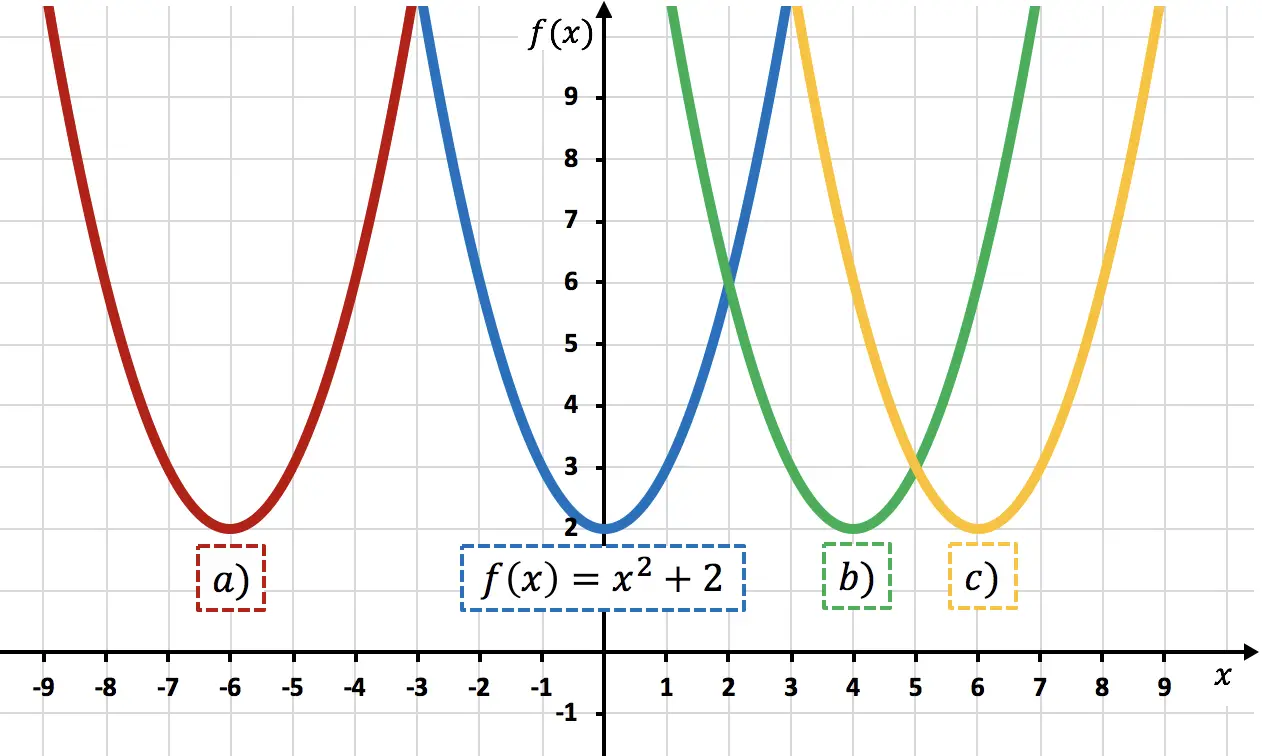
İşlev
![]()
fonksiyon
![]()
6 birim sağa kaydırıldı. Bunu hesaplayarak doğrulayabiliriz
![]()
![]()
![]()
Bu nedenle temsili
![]()
c) parabolüne karşılık gelir, çünkü 6 birim sağa kaydırılmıştır.
![]()
.
Bu, parabollerin köşelerine bakarak görülebilir: parabolün tepe noktaları arasındaki mesafe
![]()
ve c) parabolünün tepe noktası 6 birimdir, dolayısıyla ikincisi birinciye göre 6 birim sağa kaydırılmıştır.