Bir fonksiyonun kesme noktaları eksenlerle nasıl hesaplanır?

Bu sayfada bir fonksiyonun Kartezyen eksenlerle kesişme (veya kesişme) noktalarının neler olduğu ve bunların nasıl hesaplanacağı açıklanmaktadır. Ayrıca bunların nasıl bulunduğunu tam olarak anlamak için çeşitli örnekler bulacaksınız ve hatta adım adım çözülen alıştırmalarla pratik bile yapabilirsiniz.

Bir fonksiyonun eksenlerle kesişme (veya kesişme) noktaları nelerdir?

Nasıl hesaplandıklarını görmeden önce bir fonksiyonun eksenlerle kesişme noktalarının neler olduğunu hatırlayalım.

Kesişme veya eksen kesişme noktaları, bir fonksiyonun temsilinin koordinat eksenleriyle kesiştiği noktalardır, yani grafikte X ekseni ve l ekseninde bağlanan noktalardır. Y ekseni.

Örneğin, aşağıdaki grafikteki parabol, Y eksenini (0,3) noktasında, X eksenini (-1,0) ve (3,0) noktalarında kesmektedir.

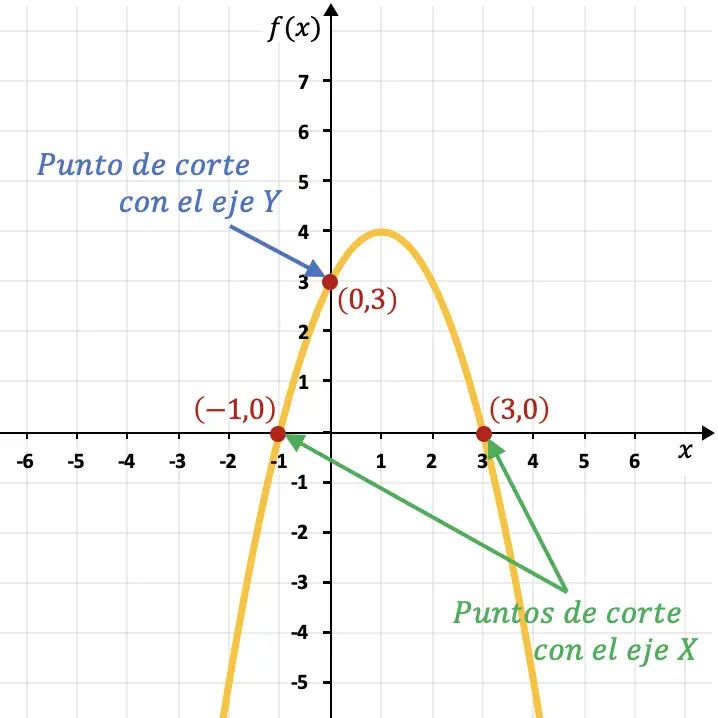
Bir fonksiyonun eksenlerle kesme veya kesişme noktaları

X eksenine sahip bir fonksiyonun kesme noktası

Bir fonksiyonun X ekseni ile kesişme noktalarının ikinci koordinatı her zaman 0 olacaktır, dolayısıyla:

Herhangi bir x ekseni fonksiyonunun (OX) kesme noktaları şu şekildedir:

$(a,0)$

ve aşağıdaki denklem çözülerek hesaplanabilir:

$f(x)=0$

Bazen bu denklemi çözerken iki (veya daha fazla) çözüm elde edebiliriz; bu, fonksiyonun X eksenini iki (veya daha fazla) kez kestiği anlamına gelir. Öte yandan denklemin çözümü yoksa bu, fonksiyonun X eksenini kesmediği anlamına gelir.

Y eksenine sahip bir fonksiyonun kesme noktası

Bir fonksiyonun Y ekseniyle kesişme noktalarının ilk koordinatı her zaman 0 olacaktır, dolayısıyla:

Y ekseni OY ile herhangi bir fonksiyonun kesme noktası şu şekildedir:

$(0,a)$

, ve fonksiyonun x=0 noktasındaki görüntüsü hesaplanarak bulunabilir:

$f(0)$

X eksenindeki kesme noktalarından farklı olarak Y ekseninde yalnızca bir kesme noktası olabilir.

Bir fonksiyonun kesme noktalarını eksenlerle hesaplama örneği

Hiç şüpheniz olmasın diye aşağıda bir fonksiyonun kesim noktalarının Kartezyen eksenlerle nasıl bulunacağına dair bir örnek göreceğiz:

Aşağıdaki fonksiyonun kesme noktalarını sayısal olarak bulun:

$f(x)=-2x+4$

İlk önce fonksiyonun kesme noktasını x ekseniyle hesaplayacağız. X ekseni ile kesişme noktasının ikinci bileşeni her zaman 0’a eşit olacaktır, yani şu türden olacaktır:

$(a,0)$

. Çünkü f(x) OX ekseninde her zaman 0’a eşittir. Noktanın diğer bileşenini bulmak için denklemi çözmemiz gerekiyor.

$f(x)=0:$

$f(x)=0$

$-2x+4=0$

$-2x=-4$

$x=\cfrac{-4}{-2}=2$

Dolayısıyla X ekseniyle kesişme noktası şu şekildedir:

$\bm{(2,0)}$

Şimdi y ekseniyle kesişme noktasını bulacağız. Y ekseniyle kesişme noktasının ilk bileşeni her zaman 0’a eşit olacaktır, yani nokta şu türden olacaktır:

$(0,a)$

. Bağımsız değişken x her zaman Y ekseninde iptal olduğundan. Yani noktanın diğer koordinatını bulmak için hesaplamamız gerekiyor.

$f(0):$

$f(0)=-2 \cdot 0+4=4$

Dolayısıyla Y ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,4)}$

Aşağıda grafiksel olarak temsil edilen örnek fonksiyonu görüyorsunuz; bulunan eşik değerlerinin grafikteki eşik değerleri ile örtüştüğünü görebilirsiniz:

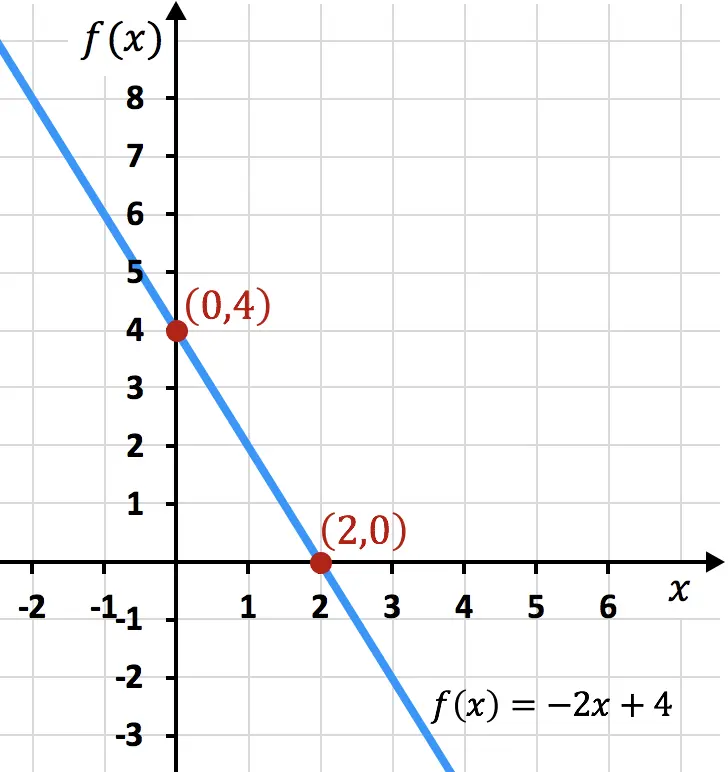
eksenli bir fonksiyonun kesme noktaları nasıl bulunur

Eksenli bir fonksiyonun kesme noktalarına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki fonksiyonun koordinat eksenlerine sahip kesme noktalarını belirleyin:

$f(x)=3x-3$

Çözümü görün

X eksenli kesme noktası

Fonksiyonun X ekseni ile kesişme noktasını bulmak için çözmek gerekir

$f(x)=0:$

$f(x)=0$

$3x-3=0$

$3x=3$

$x=\cfrac{3}{3}=1$

Dolayısıyla fonksiyonun X ekseniyle kesişme noktası şu şekildedir:

$\bm{(1,0)}$

Y ekseni ile kesme noktası

Y ekseniyle kesişme noktasını bulmak için hesaplamanız gerekir

$f(0):$

$f(0)=3\cdot 0 -3= -3$

Dolayısıyla fonksiyonun Y ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,-3)}$

Alıştırma 2

Aşağıdaki afin fonksiyonun Kartezyen eksenleriyle kesişme noktalarını bulun:

$f(x)=2x+8$

Çözümü görün

X eksenli kesme noktası

Fonksiyonun OX ekseni ile sınır noktasını bulmak için fonksiyonu sıfıra eşitlememiz ve ortaya çıkan denklemi çözmemiz gerekir:

$f(x)=0$

$2x+8=0$

$2x=-8$

$x=\cfrac{-8}{2}=-4$

Dolayısıyla fonksiyonun apsis ekseniyle kesişme noktası:

$\bm{(-4,0)}$

Y ekseni ile kesme noktası

OY ekseni ile kesme noktasını bulmak için hesaplamamız gerekir.

$f(0):$

$f(0)=2\cdot 0 +8= 8$

Dolayısıyla fonksiyonun bilgisayar ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,8)}$

Alıştırma 3

Aşağıdaki ikinci dereceden fonksiyonun eksenleriyle kesme noktalarını hesaplayın:

$f(x)=x^2-3x+2$

Çözümü görün

X eksenli kesme noktası

Fonksiyonun X ekseni ile kesişme noktasını bulmak için çözmek gerekir

$f(x)=0:$

$f(x)=0$

$x^2-3x+2=0$

Bu durumda ikinci dereceden bir denklemi çözmemiz gerekiyor, bu yüzden aşağıdaki formülü uyguluyoruz:

$\displaystyle x =\cfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

$\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}$

İkinci dereceden denklemin iki çözümünü elde ettik, böylece fonksiyon X eksenini iki noktada keser:

$\bm{(1,0)} \qquad \bm{(2,0)}$

Y ekseni ile kesme noktası

Öte yandan Y ekseni ile kesişme noktasının belirlenmesi için hesaplama yapılması gerekmektedir.

$f(0):$

$f(0)=0^2-3\cdot 0+2= 2$

Dolayısıyla fonksiyonun Y ekseniyle kesiştiği tek nokta şudur:

$\bm{(0,2)}$

Alıştırma 4

Aşağıdaki rasyonel fonksiyonun Kartezyen düzleminin eksenleriyle kesişme noktalarını bulun:

$f(x)=\cfrac{5}{x}$

Çözümü görün

X eksenli kesme noktası

Fonksiyonun X ekseni ile kesişme noktasını bulmak için çözmek gerekir

$f(x)=0:$

$f(x)=0$

$\cfrac{5}{x}=0$

$5=0\cdot x$

$5=0$

$5\neq 0$

5, 0’a eşit olmadığından denklemin çözümü yoktur ve dolayısıyla fonksiyon ile X ekseni arasında kesişme noktası yoktur.

Y ekseni ile kesme noktası

Y ekseniyle kesişme noktasını bulmak için hesaplamanız gerekir

$f(0):$

$f(0)=\cfrac{5}{0}= \infty$

Sıfıra bölünen herhangi bir sayı, sonsuzluğu veren bir belirsizliktir. Bu nedenle fonksiyon hiçbir noktada Y ekseninin ötesine uzanmaz.

Kısaca egzersiz fonksiyonunun eksenlerle kesişme noktası yoktur yani grafiği hiçbir noktada X ekseninden ya da Y ekseninden geçmemektedir.

Alıştırma 5

Aşağıdaki üçüncü derece fonksiyonun eksenleriyle kesme noktalarını hesaplayın:

$f(x)=x^3-9x$

Çözümü görün

X eksenli kesme noktası

Fonksiyonun X ekseni ile kesişme noktasını bulmak için çözmek gerekir

$f(x)=0:$

$f(x)=0$

$x^3-9x=0$

Denklemin her iki terimi de ortak bir faktör çıkarabileceğimiz bir x değerine sahiptir:

$x(x^2-9)=0$

Önceki eşitliğin sağlanması için faktörlerden birinin 0 olması gerekir. Bu nedenle tüm olası çözümleri elde etmek için her faktörü sıfıra eşitliyoruz:

$\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}$

Dolayısıyla üçüncü derece denklemin üç çözümünü elde ettik, böylece fonksiyon X eksenini 3 noktada keser:

$\bm{(-3,0)} \qquad \bm{(0,0)} \qquad \bm{(3,0)}$

Y ekseni ile kesme noktası

Y ekseniyle kesme noktasını hesaplamak için şunları hesaplamanız gerekir:

$f(0):$

$f(0)=0^3-9\cdot 0 = 0$

Bu nedenle, fonksiyonun Y ekseni ile kesiştiği tek nokta koordinat orijinidir (0,0):

$\bm{(0,0)}$

Fonksiyon bu noktada her iki eksenle aynı anda kesim yaptığı için bu noktayı X ekseniyle kesme noktasının hesaplanmasında zaten bulduğumuzu unutmayın.

Bir fonksiyonun eksenlerle kesişme (veya kesişme) noktaları nelerdir?

X eksenine sahip bir fonksiyonun kesme noktası

Y eksenine sahip bir fonksiyonun kesme noktası

Bir fonksiyonun kesme noktalarını eksenlerle hesaplama örneği

Eksenli bir fonksiyonun kesme noktalarına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et