Matematiksel gösterim, sembollerin kullanımı yoluyla fikirleri ve hesaplamaları iletmenin bir yoludur. İlk bakışta kafa karıştırıcı gibi görünse de, biraz pratik yaparak kolaylıkla yorumlayabileceksiniz. Bu yazıda size bu gösterimde kullanılan tüm simgelerin anlamlarını ve bunların nasıl uygulanacağına dair bazı örnekleri göstereceğiz.
Matematiksel gösterim nedir?
Matematiksel gösterim, matematikte kullanılan değerleri ve ifadeleri yazmanın bir yoludur. Bu teknik, matematikçilerin fikirleri kısa ve net bir şekilde ifade etmelerine olanak tanır. Matematik gösterimi aynı zamanda matematik uygulayan veya matematik üzerine çalışan kişilerin kavramları daha iyi anlamalarına da olanak tanır.
Matematik dili, sayısal değerleri yazmanın bir yolu olan bilimsel gösterimle karıştırılmamalıdır. Bu arada matematiksel gösterim, tıpkı bir dil gibi, karmaşık ifadeler yazmanıza olanak tanıyan bir dizi sembolden ibarettir. Bu konuya daha sonra daha detaylı olarak döneceğiz.
Matematiksel gösterim nasıl okunur?
Matematiksel gösterimi yorumlamayı öğrenmek göründüğünden daha kolaydır; yalnızca her sembolün anlamını öğrenmeniz gerekir ve bunu bir kez öğrendikten sonra matematiksel gösterimle yazılmış her şeyi okuyabileceksiniz. Açıkçası pratik ve çok fazla çalışma süresi gerektirmesine rağmen, bu kadar basit.
Matematiksel ifadeler çok mantıklıdır ve her zaman kalıpları takip eder, bu nedenle sadece kuralları ezberlemeniz yeterlidir ve daha sonra bunları herhangi bir duruma nasıl çıkaracağınızı bileceksiniz. Hatta çok karmaşık hesaplamaları bile tanımlayabiliriz; bu, çok ayrıntılı mesajların metodik bir şekilde iletilmesini sağlayan matematik dilinin büyüsüdür.
Matematiksel Gösterimin Bileşenleri
Matematiksel gösterim; sayıları, işlemleri ve bunlar arasındaki ilişkileri temsil eden bir dizi sembolden oluşur. Bu semboller ilk başta karmaşık görünebilir, ancak biraz pratik ve anlayışla matematiksel gösterimi yorumlamak çocuk oyuncağı haline gelecektir.
Daha sonra matematik dilinde bulunabilecek dört tür öğeyi ayrıntılı olarak açıklayacağız. En temelden başlayıp en karmaşık ve soyut olanla biten. Teorik açıklama bittiğinde, var olan sayısal gösterim türlerinden bahsedeceğiz.
Sayılar ve sayı kümeleri
Öncelikle matematiksel sayıları tanımlamamız gerekiyor, bir birimle ilgili miktarı belirten matematiksel bir kavramdır. Ondalık sayı sistemini takip ederek ve şu sembolleri birleştirerek herhangi bir sayısal değeri tanımlayabiliriz: 0, 1, 2, 3, 4, 5, 6, 7, 8 ve 9.
Sayıları farklı özelliklerine göre sıralarsak, sayı kümeleri adı verilen çeşitli sayı kategorileri elde ederiz. Ve bu değer gruplarının da kendilerini belirten kendi sembolleri vardır; aşağıdaki listede hepsini karşılık gelen grubun adıyla sunuyoruz:
- ℙ: asal sayılar
- ℕ: doğal sayılar
- ℤ: Bütün
- ℚ: rasyonel sayılar
- ℝ: Gerçek sayılar
- 𝕀: sanal sayılar
- ℂ: karmaşık sayılar
- ℍ: Kuaterniyonlar
Bu semboller genellikle hesaplamalarımızda geniş bir sayı aralığını aynı anda belirlemek için kullanılır. Örneğin elimizde birçok değeri buna göre kabul eden bir ifade varsa sayıları tek tek yazmak yerine bu değerleri sayısal gruplarına karşılık gelen sembol aracılığıyla belirtmemiz daha kolay olacaktır.
Operatörler ve niceleyiciler
Matematiğin özü olan sayıları ele aldığımıza göre artık operatörler ve niceleyicilerden bahsetmemiz gerekiyor. Bunlardan ilki, bir işlemi temsil etmemizi sağlayan tüm sembollerdir: toplama (+), çıkarma (-), çarpma (x veya ·), bölme (÷), ve diğerleri.
Ancak mantıksal operatörler ve ilişkisel operatörler olmak üzere iki tür operatörümüz daha vardır. Birincisi bağlacı, ayrılığı ve olumsuzlamayı ifade eder. Aritmetik işlemlerden farklı olarak sayılarla değil matematiksel önermelerle çalışan mantıksal işlemler önermemize yardımcı olurlar.
İkincisi ise değerler veya matematiksel ifadeler arasında denklikler ve ilişkiler kurmamızı sağlar. Bu semboller aritmetik hesaplamalarda (sayıları sıralamak için) kullanılabilir, ancak değişkenlerimiz olduğunda cebirde daha önemlidirler (bu konuda daha fazla bilgi iki bölümde yer alır).
Aşağıdaki listede şu ana kadar tartıştığımız tüm operatörlerin tanımını bulabilirsiniz:
| Sembol | Tanım | tür |
| + | Ek | aritmetik operatörü |
| – | Çıkarma | aritmetik operatörü |
| X, *, · | Çarpma işlemi | aritmetik operatörü |
| ÷ | Bölüm | aritmetik operatörü |
| x² | yetkilendirme | aritmetik operatörü |
| √ | Depozito | aritmetik operatörü |
| VE | Bağlaç | mantıksal operatör |
| HERHANGİ BİRİ | Ayrılık | mantıksal operatör |
| HAYIR | İnkar | mantıksal operatör |
| = | Eşittir | ilişki operatörü |
| > | Daha büyük | ilişki operatörü |
| < | Daha küçük | ilişki operatörü |
| >= | Daha iyi veya eşit | ilişki operatörü |
| <= | küçük veya eşit | ilişki operatörü |
| ≠ | eşit değildir | ilişki operatörü |
| ≡ | Tam olarak aynı | ilişki operatörü |
| ≈ | neredeyse eşit | ilişki operatörü |
| ≃ | Eşittir | ilişki operatörü |
| ∝ | Orantılı | ilişki operatörü |
Matematiksel mantığı küme teorisinden açıklamak için kullanılan beş mantıksal operatör daha olmasına rağmen. Hesaplamada, geometride, istatistikte kullanılan küme mantığını uygulayan bir dal… Daha sonra size kullanılan sembolleri ve tanımlarını gösteriyoruz.
| Sembol | Tanım |
| x ∈ Bir | x A’ya aittir |
| x ∉ Bir | x A’ya ait değil |
| ∪ | birlik |
| ∩ | Kavşak |
| ⊂ | Dahil etme |
Niceleyicileri ise belirli bir koşulu (eşdeğerlik, sıra, üyelik vb.) sağlayan bir kümenin eleman sayısını gösteren simgeler olarak tanımlayabiliriz. Çok çeşitli operatörler vardır, ancak en çok kullanılanlar arasında şunları vurgulayabiliriz:
| Sembol | Tanım | tür |
| ∀x | tüm x’ler için | ölçmek |
| ∃x | En az bir x var | ölçmek |
| ∄x | x yok | ölçmek |
| ∃!x | Sadece bir tane x var | ölçmek |
| | | Örneğin | ölçmek |
| ∴ | BU YÜZDEN | ölçmek |
Matematiksel ifadeler ve ilişkileri
Şu ana kadar ele aldığımız sembollerle matematiğin çoğunu anlayabilirsiniz, ancak henüz bunların uygulamalarını veya karmaşık ifadelerdeki ilişkilerini (birleşik işlemler veya cebirsel hesaplamalar gibi) açıklamadık. Ayrıca hâlâ tartışılacak ilişki sembolleri var. Bu bölümde göreceğimiz bunlar.
Gruplandırma sembollerinden başlayarak bunlar parantez, köşeli parantez ve küme parantezleridir. Bu unsurlar karmaşık formüllerin belirlenmesinde önemlidir. Ana işlevi, küresel bir ifade dahilinde belirli hesaplamalara öncelik vermektir . Ve üç tür arasında farklı öncelik seviyeleri vardır. Bu ifadede 3 {[2 + (3 – 2) · 2] – 4} yazma sırasını görebilirsiniz.
| semboller | Tanım | Öncelik |
| “(“Ve”)” | Parantez | Maksimum öncelik |
| “[“Ve”]” | Parantez | ikinci öncelik |
| “{” Ve “}” | Anahtarlar | üçüncü öncelik |
Bu kategoriyi bitirmek için tekrarlanan toplama ve çarpma işlemlerini tanımlamamıza olanak sağlayan öğeler olan toplamlar (Σ) ve çarpımlardan (∏) bahsedeceğiz. Toplama şunu söylemeye eşdeğerdir: “i’nin 1’den an’a kadar değerleri aldığı Xi’nin toplamı”. Ve sonuç aynı ama eklemek yerine çarpıyoruz.
cebirsel analiz
Cebirsel sembollerle ilgili tartışılacak ilk şey, alfabenin harfleriyle temsil edilen değişkenlerdir. Görevleri bir sayıyı taklit etmektir ancakmatematiksel sabitler gibi sabit bir değerleri yoktur, dolayısıyla yeni değerler alabilirler. Bu denklemler, limitler, türevler, integraller, matrisler için geçerlidir…
Son olarak, bu son paragrafta bahsettiğimiz tüm bu cebirsel işlemlerin temsillerinden bahsetmek istiyoruz. O zamandan beri bunlar cebirin temelidir ve onların sembollerinin ne olduğunu bilmeniz gerekir. Daha sonra size farklı sembolleri ve kısa tanımlarını içeren bir tablo göstereceğiz:
| Sembol | Tanım |
| lim x → b | Limit (x, b’ye doğru yöneldiğinde) |
| y’, ƒ’ (x), dy / dx | türev |
| ∫ | Tamamlamak |
| mxn’ye | Mxn boyutlarının matrisi |
Matematik dilinin sembolleri üzerine sonuç
Şu ana kadar matematiğin kapsadığı tüm önemli sembolleri gördünüz, elbette tartışılacak daha çok şey var. Ancak bunlar matematiğin her alt kategorisine özeldir : geometri, istatistik, cebir… Bu nedenle bu konuyu kapatıp sayısal gösterimlerden bahsedeceğiz.
Sayısal gösterim türleri
Bu bölümde matematiksel sayıları ifade etmenin tüm yollarını göreceğiz çünkü bunu yapmak için farklı gösterimler vardır. Yukarıda matematikçilerin en çok kullandığı ondalık sayı sisteminden bahsetmiştik. Daha sonra bunu daha ayrıntılı olarak açıklayacağız ve size diğer matematiksel gösterim türlerini göstereceğiz:
ondalık gösterim
Ondalık sayı sistemi, 10 sayısının katlarına ve alt katlarına dayanan konumsal bir sayı sistemidir (her basamağın konumunun değerini belirleyeceği sistem). Çünkü on , sayısal taban olarak kullanılan sayıdır. Bu nedenle kullanacağımız on sayı sembolü şunlardır: 1, 2, 3, 4, 5, 6, 7, 8, 9 ve 0.
Bu sayıların değeri , konuma göre oluşturulan onluk tabandaki kuvvetlerin rakamlarının toplamı ile çarpılarak bulunur. Ve birden küçük bir sayı yazarken virgülün kullanılması gerektiğini hatırlamanız çok önemlidir. Aşağıda bir örnek verilmiştir:
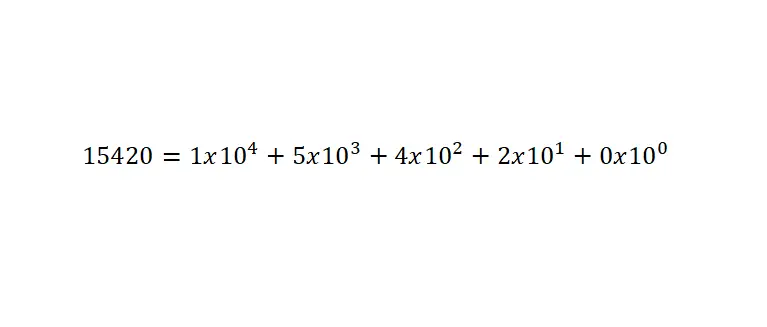
Bilimsel gösterim
Üstel form gösterimi veya bilimsel gösterim , bilim ve teknolojide açıkça en çok kullanılan yazı türlerinden biridir. Aslında bu çok büyük ve çok küçük sayıları basit bir şekilde ifade etmemizi sağlar. Bilimsel gösterimin tanımını anlamak için bir tam sayının bu gösterime nasıl aktarılacağını açıklayacağız:
- Ondalık noktayı taşıma: İlk basamağa ulaşana kadar ondalık noktayı gerektiği kadar hareket ettirmelisiniz (çok büyük bir sayınız varsa sola, çok küçük bir sayınız varsa sağa).
- Tabanı oluşturun: Bu son sayıyı on ile çarparak yazın, yani virgülünü bir tarafa kaydırarak elde ettiğiniz değerin yanına on ile çarpma yazmalısınız: “x 10”.
- Bir üs ekleyin: ondalık noktayı hareket ettirme sayısına eşit bir değere sahip. Büyük sayılarda üssü pozitif olarak bırakacaksınız, ancak küçük sayılarda üssü negatif işaretle yazmalısınız.
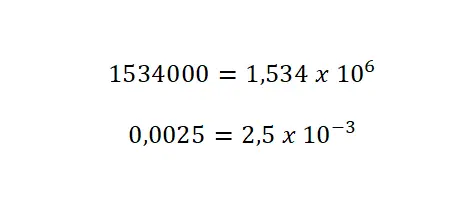
onaltılı gösterim
Onaltılık sistem 16’yı temel alır, yani on altı farklı sembol kullanır: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E ve F. bakın bu numaralandırma sistemi ondalık sistemdeki rakamlardan ve altı harften oluşuyor. Bu gösterim genellikle özellikle BT’de ve BT ile ilgili her şeyde kullanılır.
Diğer gösterim türleriyle ortak sembollere sahip olduğundan, her zaman parantez ve indeks 16 aracılığıyla onaltılık sistemde yazıldığını belirtmemiz gerektiğini açıklığa kavuşturmak önemlidir. Aşağıdaki örnekte, onaltılık bir sayının ondalık gösterime dönüştürülmesini çok açık bir örnekten görebilirsiniz:
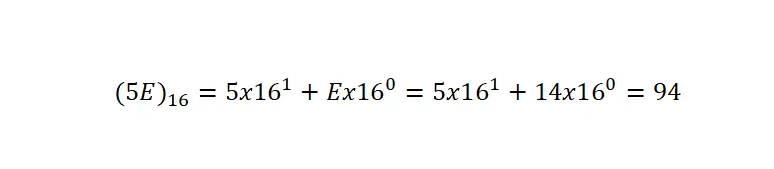
Onaltılık bir sayıyı ondalık ifadeye dönüştürmek için, ondalık gösterimde yaptığımız gibi sayıyı taban çarpımlarına ayırmamız, ancak tabanı 16 olarak değiştirmemiz gerekir. Daha sonra, her rakamı, söz konusu rakamın eksi bir olduğu konuma yükseltilmiş on altı ile çarpacağız.
sekizlik gösterim
Bahsedeceğimiz son sistem, tabanı 8 olan sekizlik gösterimdir . Bu, yalnızca sekiz simge veya sayı kullandığı anlamına gelir: 0, 1, 2, 3, 4, 5, 6 ve 7. en az kullanılanıdır. anlattıklarımızın hepsinin numaralandırma sistemi. Bu notasyonun dönüşümlerinin öncekilerle aynı prosedüre göre gerçekleştirildiğine dikkat edilmelidir.
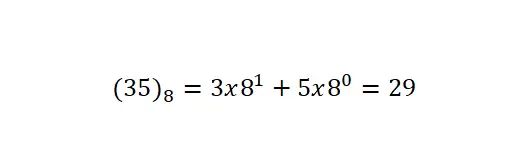
roman notasyonu
Son olarak günümüzde pek kullanılmayan ancak geçmişte matematik alanında oldukça önemli olan Romen rakamı sisteminden bahsedebiliriz. Çünkü matematiğe hayat veren notasyonlardan biriydi.
Yazınız 7 sembolle sınırlıdır: I (1), V (5), X (10), L (50), C (100), D (500) ve M (1000). Ve bu harflerin birleştirilmesiyle tüm sayılar yazılıyor. Bunların nasıl bir araya gelerek daha büyük sayılara yol açtığını öğrenmek istiyorsanız, son bağlantıdan erişerek onlar hakkındaki makalemizi okumanızı öneririz.
Matematiksel gösterimde okuma performansı nasıl geliştirilir?
Matematik gösterimini okuma performansını artırmanın birkaç yolu vardır. Bunun bir yolu sembolleri ve sayıları yüksek sesle okumaktır. Başka bir yol da sembollere ve anlamlarına aşina olmaktır. Ayrıca alıştırmalar ve problemler kullanarak matematik notalarını okuma pratiği yapabilirsiniz.
Umarız bu rehberle size yardımcı olmuşuzdur, lütfen herhangi bir sorunuz varsa yorumlara yazmaktan çekinmeyin. Ya da konuya katkı sağlamak isterseniz onu da yorumlarda görmeyi umuyoruz. Bununla birlikte, okumaya devam etmek isterseniz size matematiğin nasıl öğrenileceğine dair bir makale bırakıyoruz.