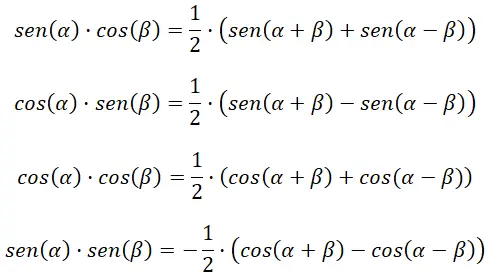Trigonometrik kimlikler, farklı trigonometrik fonksiyonlar arasındaki eşitliklerdir. Bu trigonometrik eşdeğerlikler sayesinde herhangi bir diğerine dayalı olarak belirli birtrigonometrik oran çıkarımı yapabiliriz. Dolayısıyla trigonometrik özdeşliklerin formüllerini anlayabilmek için bu oranların formüllerini bilmek gerekir. Sizin durumunuzda bunları bilmiyorsanız son bağlantıyı ziyaret etmenizi öneririz.
Trigonometrik kimlikler tablosu
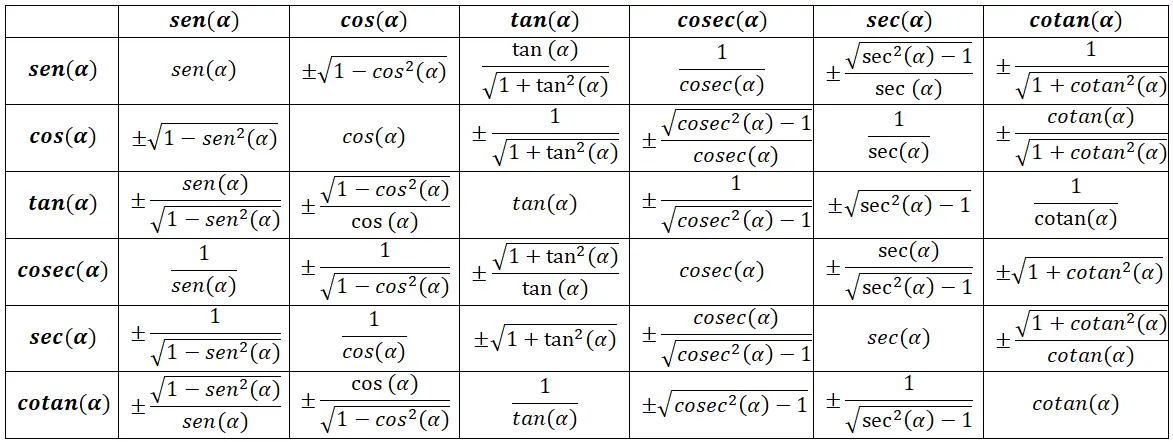
Temel trigonometrik kimlikler
Diğerleri için teorik temel oluşturdukları için en önemlileri kabul edilen bir dizi temel trigonometrik kimlik vardır. Bunlar, oldukça sezgisel oldukları için bulunması en yaygın olanlardır ve muhtemelen hatırlanması en kolay olanlardır. Tüm formüllerin aşağıdaki resme dayanacağını unutmayın:

Temel trigonometrik kimlik
Hepsinin ilk özdeşliği, sinüs ve kosinüs arasındaki ilişki olarak da bilinen temel trigonometrik özdeşlik olarak bilinen şeydir. Matematiksel kanıtı aşağıdadır: sin² (α) + cos² (α) = 1.
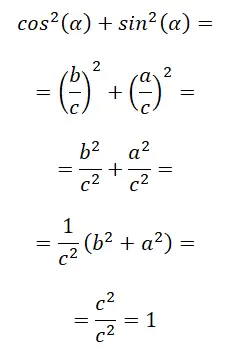
Son adımda temel olarak Pisagor teoremini uyguluyoruz, çünkü c² = a² + b² elimizde c² / c² yani 1 kalıyor. Sonuç olarak şunu söyleyebiliriz: sin² (α) + cos² (α) = 1.
Kesen ve teğet arasındaki ilişki (sekantın karesi)
İkinci olarak, sekantı teğete bağlayan trigonometrik bir özdeşliğe sahibiz, ifadesi şu şekildedir: sec² (α) = 1 + tan² (α) . Aşağıdaki resimde bu kimliği oluşturan bazı hatırlatma formüllerini ve ardından nihai formüle ulaşmak için izlenecek prosedürü görebilirsiniz:
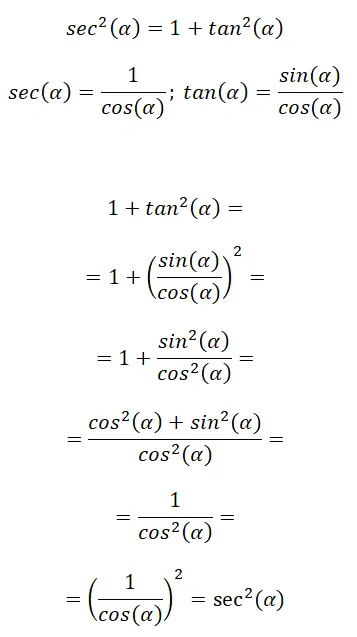
Bu durumda diğer oranları bulmak için trigonometri oranı formüllerini kullanırız. Sonuç olarak şunu söyleyebiliriz: sn²(α) = 1 + tan²(α).
Kosekant ve kotanjant arasındaki ilişki (kosekant kare)
Kosekant ve kotanjantın tanımından teğet formülünde bir bağlantı bulabiliriz, bu sayede başka bir trigonometrik özdeşlik çıkarabiliriz: cosec² (α) = 1 + cotg² (α) .
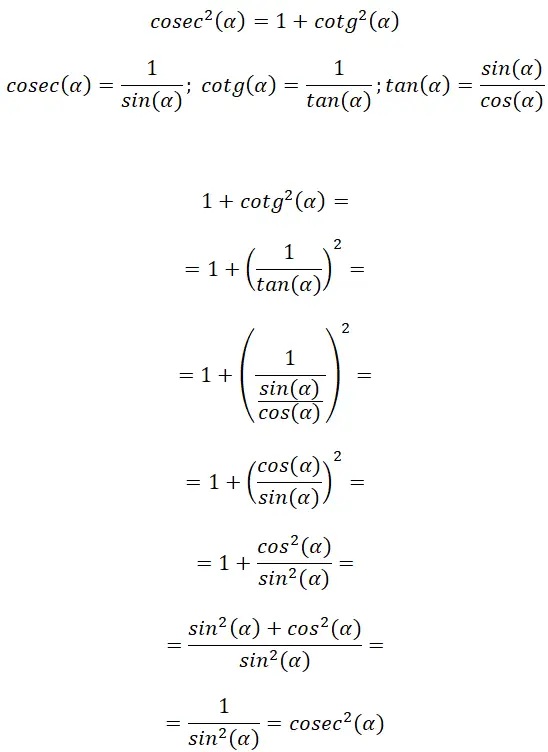
Bu gösterimle şunu doğrulayabiliriz: cosec² (α) = 1 + cotg² (α). Ek olarak, bu ilişkinin bir öncekiyle bazı benzerlikler taşıdığını da görebiliriz, bu da teğet ve kotanjant arasındaki benzerlikten kaynaklanmaktadır.
Toplam açı ve çıkarma açısının trigonometrik oranları
Açı toplamı veya açı çıkarma oranları, iki açının toplanması veya çıkarılmasının trigonometrik oranlarının hesaplanmasıyla elde edilen bir kimlik türüdür. Örneğin 90 + 60’ın sinüsünü hesaplamak istiyorsak bu hesaplamayı kolaylaştıran bir dizi formül vardır. Aşağıda bu stildeki trigonometrik özdeşliklerin tüm formüllerini içeren bir liste bulunmaktadır:
Açıların toplamının sinüsü: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Açının sinüsü çıkarma: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Açıların toplamının kosinüsü: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Açısal kosinüsün çıkarılması: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Açıların toplamının tanjantı: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
Açısal tanjant çıkarma: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))
150°’nin sinüsünü hesaplamanın, (90° + 60°) sinüsünü hesaplamak için az önce açıkladığımız formülleri kullanmaktan daha kolay olduğu açıktır. Peki bu formüller neden önemli? Cevap, bu özdeşliklerin karmaşık açıların trigonometrik oranlarını daha basit açılardan hesaplamamıza olanak sağlamasıdır. Bu nedenle, dikkate değer (en alakalı) açıların oranlarını ezberlersek, 150° gibi daha karmaşık açıların oranlarını hesaplamak için hesap makinesini kullanmamıza gerek kalmayacaktır.
Çift açılı trigonometrik oranlar
Bir çift açının (2α) trigonometrik oranlarını hesaplamak istediğimizde bunu bir dizi özdeşlik aracılığıyla yapabiliriz. Daha doğrusu bunu önceki bölümde tartıştığımız formüllere çok benzer formüllerle yapabiliriz. Çünkü önceki ifadelerde β’yı α olarak değiştirirsek elimizde (2α)’ya eşdeğer olan (α + α) kalır. Bunu akılda tutarak aşağıdaki kimlikleri türetebiliriz:
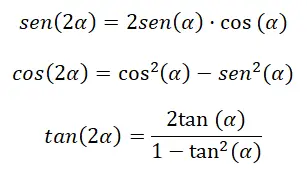
Demoları aşağıda görebilirsiniz:
Çift açının sinüsü: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Çift açının kosinüsü: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Çift teğet açısı: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
Yarım açının trigonometrik oranları
Ayrıca yarım açının (α/2) trigonometrik oranlarını hesaplamamızı sağlayan özdeşlikler vardır:
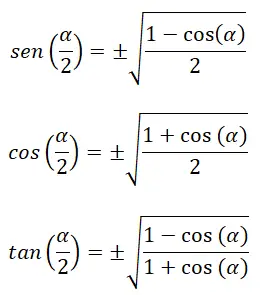
Aşağıdaki zaten bilinen formüller arasında:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
Eğer β = α/2 yaparsak, sinüs durumunda iki ifadeyi çıkararak, kosinüs durumunda toplayarak ve elde edilen iki formülü (sinüs ve kosinüs formülü) bölerek bu özdeşlikleri kanıtlayabiliriz. teğet durumunda. Ancak aşağıda elde ettiğimiz formüllerde hesaplamak istediğimiz oranı izole etmek kalıyor:
Yarım sinüs açısı: 1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) ÷ 2
Yarım açılı kosinüs: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
Üçlü açının trigonometrik oranları
Üçlü açının (3α) olması durumunda, trigonometrik oranlarını hesaplamak için belirli özdeşlikleri de kullanabiliriz. Bu özdeşlikler daha önce açıklanan formüllerden gelir: çift açı özdeşlikleri, toplam açı özdeşlikleri ve trigonometrinin temel özdeşliği.
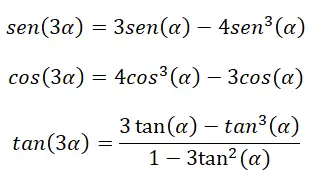
Bu özdeşlikleri kanıtlamak için açı toplamı formüllerini kullanmalıyız:
Açıların toplamının sinüsü: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Açıların toplamının kosinüsü: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Yani az önce bahsettiğimiz ifadelerdeki çift açı formüllerini uygularsak ve trigonometrinin temel özdeşliğini uygularsak özdeşlikleri ispatlayabiliriz. Temel trigonometrik özdeşliğin kullanılmasının, ifadedeki tüm oranları bire dönüştürmemize olanak sağladığını belirtmekte fayda var. Bu nedenle üçlü açının sinüs formülü yalnızca sinüslerden oluşur ve kosinüs formülü yalnızca kosinüsleri içerir. Aşağıda prosedürün tamamını görebilirsiniz:
Üçlü açının sinüsü: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin³ (α) – sin³ (α) + 2 sin (α) – 2 sin³ (α) =
= 3 sin (α) – 4 sin³ (α)
Üçlü açının kosinüsü: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Son olarak, üçlü açının tanjantı iki şekilde hesaplanabilir: birincisi sinüs formülünü kosinüs formülüne bölerek ve ikincisi çift açının tanjantı ifadesini aşağıdaki formülde tanjantla değiştirerek toplam açı: tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) tan (2α)).
Açı türüne göre trigonometrik özdeşlikler
Bir bakıma trigonometrik oranların doğrudan ve hızlı hesaplanmasına izin veren kurallar olan bir dizi formül hakkında yorum yapmak önemlidir. Aslında az önce bahsettiğimiz tüm ifadelerle aynı özellikleri taşıdıkları için trigonometrik özdeşlikler de sayılabilirler. Daha doğrusu bu formüller bir açının diğer açıyla olan ilişkisinden trigonometrik ilişkilerini belirlememizi sağlar.
Tamamlayıcı açılar
Tümler açılar (α ve β ) toplamı 90° olan açılardır, dolayısıyla bunları eklediğimizde dik açı elde ederiz. α’nın β’nın tamamlayıcı açısı olduğunu belirlemek için çok basit bir denklem çözmeliyiz: α = 90 – β , eğer bu denkliğin sonucu uyuşuyorsa, o zaman bunların tamamlayıcı olduğunu doğrulayabiliriz. Bu özdeşlikler sayesinde bir açının trigonometrik oranlarını diğer açının trigonometrik oranlarından çıkarabiliriz.
Tümler açının sinüsü: sin (90° – α) = cos (α)
Tümler açının kosinüsü: cos (90° – α) = sin (α)
Tümler açının tanjantı: tan (90° – α) = cotan (α)
Tamamlayıcı açının kosekantı: kosek (90° – α) = sn (α)
Tümler açının sekantı: sn (90° – α) = kosec (α)
Tümler açının kotanjantı: cotan (90° – α) = tan (α)
ek açılar
Ek açılar (α ve β ), toplamı 180° veya π radyana eşit olan açılardır, dolayısıyla α + β = 180° formülünü çıkarabiliriz. Veya başka bir deyişle, α’nın bütünler açısı β ise aşağıdaki β = 180 – α ifadesinin karşılanması gerekir. O zaman şu açılardan çıkarım yapabileceğimiz kimliklerin listesini görebilirsiniz:
Tümler açının sinüsü: sin (180° – α) = sin (α)
Ek açının kosinüsü: cos (180° – α) = -cos (α)
Tümler açının tanjantı: tan (180° – α) = -tan (α)
Ek açının kosekantı: kosek (180° – α) = kosek (α)
Tümler açının sekantı: sn (180° – α) = -sn (α)
Tümler açının kotanjantı: cotan (180° – α) = -cotan (α)
eşlenik açılar
Eşlenik açılar (α ve β ), toplamı 360° veya 2π radyana eşit olan açılardır, bu nedenle α + β = 360° formülünü çıkarabiliriz. Ve bu ilk formülden açılardan birini diğerine göre şu şekilde ifade edebiliriz: α = 360° – β veya β = 360° – α. Şimdi size eş açıların eşitliklerini göstereceğiz:
Eşlenik açının sinüsü: sin (360° – α) = – sin (α)
Eşlenik açının kosinüsü: cos (360° – α) = cos (α)
Eşlenik açının tanjantı: tan (360° – α) = – tan (α)
Eşlenik açının kosekantı: kosek (360° – α) = – kosek (α)
Eşlenik açının sekantı: sn (360° – α) = sn (α)
Eşlenik açının kotanjantı: cotan (360° – α) = – cotan (α)
zıt açılar
Karşıt açılar veya negatif açılar (α ve β ), aynı sayısal değere sahip ancak farklı işaretlere sahip olan açılardır; bu tür açılara örnek olarak 30° ve -30° verilebilir. Negatif işaretin dönüşün saat yönünde olduğunu, pozitif açının ise saat yönünün tersine döndüğünü gösterdiği unutulmamalıdır.
Karşı açının sinüsü: sin (-α) = – sin (α)
Karşı açının kosinüsü: cos (-α) = cos (α)
Karşı açının tanjantı: tan (-α) = – tan (α)
Karşı açının kosekantı: kosek (-α) = – kosek (α)
Karşı açının sekantı: sn (-α) = sn (α)
Karşı açının kotanjantı: cotan (-α) = – cotan (α)
90°’den farklı açılar veya artı/eksi π/2 açıları
90° farkı olan açılar veya artı/eksi π/2 (α ve β ) açıları 90° farkı olan açılardır. Bu nedenle β – α = 90° olarak ifade edilebilirler; burada β, α’dan 90° daha büyüktür. Bu açılar aynı zamanda iki açının trigonometrik oranlarını ilişkilendiren bir dizi formüle de sahiptir.
90°’den farklı olan açının sinüsü: sin (90° + α) = cos (α)
90°’den farklı olan açının kosinüsü: cos (90° + α) = -sin (α)
90°’den farklı olan açının tanjantı: tan (90° + α) = – cotan (α)
90°’den farklı olan açının kosekantı: kosek (90° + α) = sn (α)
90°’den farklı olan açının sekantı: sn (90° + α) = -cosec (α)
90°’den farklı olan açının kotanjantı: cotan (90° + α) = -cotan (α)
180°’den farklı açılar veya artı/eksi π açıları
Artı/eksi açılar π (α ve β ), aralarında 180° fark olan açılara eşdeğerdir. Bu nedenle aşağıdaki formül kullanılarak ifade edilebilirler: β – α = 180°, burada β 180°, α’dan büyüktür. Daha sonra size bu açıların trigonometrik oranlarını ilişkilendiren trigonometrik özdeşlikleri göstereceğiz:
180°’den farklı olan açının sinüsü: sin (180° + α ) = -sin ( α )
180°’den farklı olan açının kosinüsü: cos (180° + α ) = -cos ( α )
180°’den farklı olan açının tanjantı: tan (180° + α ) = tan ( α )
180°’den farklı olan açının kosekantı: kosec (180° + α ) = -cosec ( α )
180°’den farklı olan açının sekantı: sn (180° + α ) = -sn ( α )
180°’den farklı olan açının kotanjantı: cotan (180° + α ) = cotan ( α )
Trigonometrik oranların dönüşümleri
Son olarak belirli bir trigonometrik oranı diğer işlemlerle ifade etmemizi sağlayan trigonometrik özdeşlikler vardır. Yani elimizde bir oranlar toplamı varsa ve bunu çarpım olarak ifade etmek istiyorsak bu formüllere başvurabiliriz. Ne yazık ki her aritmetik işlem için bir ifade olmamasına rağmen, yalnızca toplama veya çıkarmadan çarpıma veya tam tersi şekilde gidebilirsiniz.
Toplama veya çıkarma işlemini çarpıma dönüştürün
Aşağıdaki dört formül trigonometrik fonksiyonların toplama ve çıkarma işlemlerini hesaplamamıza yardımcı olur:
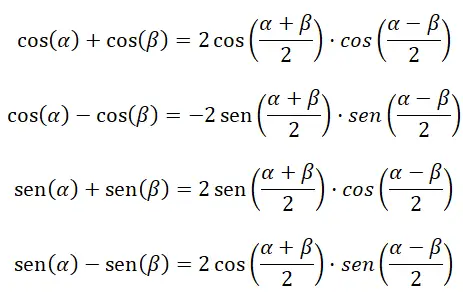
Ürünü toplama veya çıkarmaya dönüştürün
Aşağıdaki dört formül trigonometrik fonksiyonların çarpımlarını hesaplamamıza yardımcı olur: