Bir açının trigonometrik oranları, bir dik üçgenin üç kenarından elde edilen oranlardır. Başka bir deyişle bunlar, üç tarafının bölümler (bölümler) kullanılarak karşılaştırılması sonucu ortaya çıkan değerlerdir. Ancak bu nedenlerin yalnızca dik üçgenlerde (açısı 90° olan üçgenlerde) mevcut olduğunu belirtmek gerekir.
Dik üçgende trigonometrik oranlar
En önemli altı trigonometrik oran şunlardır: sinüs, kosinüs, tanjant, kosekant, sekant ve kotanjant. Daha sonra bu nedenlerin her birinin nasıl tanımlandığını ayrıntılı olarak açıklayacağız ve bunları karakterize eden formülden bahsedeceğiz. Aşağıdaki açıklamaları anlamak için aşağıdaki dik üçgeni dikkate alacağız:

Göğüs
Bir açının sinüsü (sin veya günah), karşı bacağın (a) hipotenüs (c) arasındaki bölümüne eşittir, bu nedenle sinüs formülü şu şekildedir: sin (α) = a / c . Sinüs tanımını bilmek çok önemlidir çünkü bu, bu bölümde ele alacağımız diğer nedenlerin yanı sıra tüm trigonometrinin temelidir.
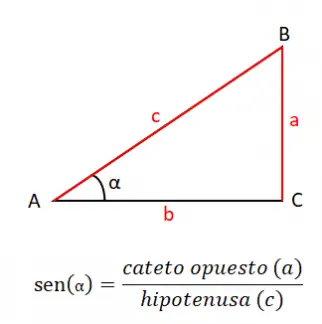
Trav Sinüs teoreminden üçgenin herhangi bir kenarını hesaplayabiliriz, bunu belirli bir açının bölümlerini karşılık gelen kenar arasına bağlayarak yapabiliriz. Örneğin, a kenarını hesaplamak istiyorsak ve A ve B açılarına göre yan değerlerimiz varsa, bunu şu formülü kullanarak yapabiliriz: a / sin (A) = b / sin (B) . Bu basit denklemi çözerek hesaplamak istediğimiz değişkene karşılık gelen değeri elde ederiz.
Kosinüs
Bir açının kosinüsü (cos), bitişik bacağın (b) hipotenüs (c) arasındaki bölümüne eşittir, bu nedenle kosinüs formülü şöyledir: cos (α) = b / c . Bu durumda formül, incelemek istediğimiz açıyla, bu örnekte A veya α açısıyla temas halinde olan üçgenin iki kenarından oluşur.
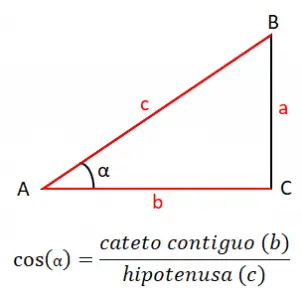
Kosinüs ile, kosinüs teoreminden gelen üçgenin kenarlarını hesaplamanın bir yöntemine de sahibiz. Bu, kenarları açılara bağlamamızı sağlar ve bize aşağıdaki üç ifadeyi verir:
a² = b² + c² – 2bc çünkü (A)
b² = a² + c² – 2ac çünkü (B)
c² = a² + b² – 2ab çünkü (C)
Teğet
Orijinal nedenler kümesini kapatacağımız üçüncü en önemli neden ise teğettir (tan veya tg). Bu, karşı bacak (a) ile bitişik bacak (b) arasında bölünerek hesaplanır, dolayısıyla teğet formülü şu şekildedir: tan (α) = a / b . Aşağıda grafiksel olarak görebilirsiniz:
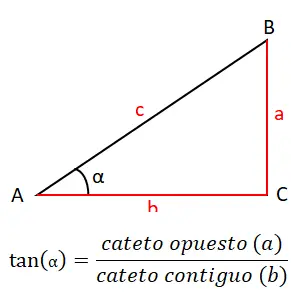
Teğetin ayrıca teğet teoremi adı verilen kendi teoremi vardır. Bu bize bir üçgenin iki kenarının uzunluğunu açıların teğetleriyle ilişkilendirmemizi sağlar. İfade şu şekildedir: “İki kenarın toplamının çıkarılmaları arasındaki bölümü, bu kenarların karşısındaki iki açının ortalamasının tanjantına ve bunların yarısı farkının tanjantına eşittir”.
Türetilmiş trigonometrik oranlar
Az önce tartıştığımız üç trigonometrik orandan türetilen diğer trigonometrik oranları elde edebiliriz. Bunlar sinüs, kosinüs ve tanjanta göre ters oran alınarak elde edilir.
- Kosekant: sinüsün ters oranıdır ve şu formüllerle hesaplanır: kosek (α) = c/a ve kosek (α) = 1/sin (α).
- Sekant: kosinüsün ters oranıdır ve sec (α) = c/b ve sec (α) = 1 / cos (α) formülleriyle hesaplanır.
- Kotanjant: tanjantın ters oranıdır ve şu formüllerle hesaplanır: cotg (α) = b/a ve cotg (α) = 1 / tan (α).
Trigonometrik oranlar tablosu
Aşağıda şu ana kadar açıklanan tüm nedenleri özetleyen bir tablo görebilirsiniz. Bu tabloyla tüm formülleri etkili bir şekilde ezberleyebileceksiniz çünkü her matematiksel ifade arasındaki farkları kolayca ayırt etmenizi sağlıyor.
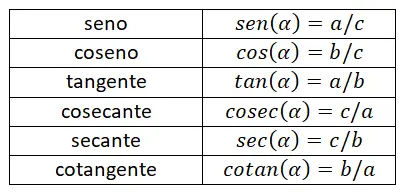
Bir dairedeki trigonometrik oranlar
Trigonometriyi çalışmanın başka bir yolu da gonyometrik çevre veya birim çemberdir; bu çevrenin yarıçapı 1’e eşittir ve kökeni (0, 0) noktasıdır. Çizim bir daire ve dairenin içinde gösterilen bir dik üçgenden oluşur, daha doğrusu inceleyeceğimiz açının orijinal noktaya değmesi gerekir.
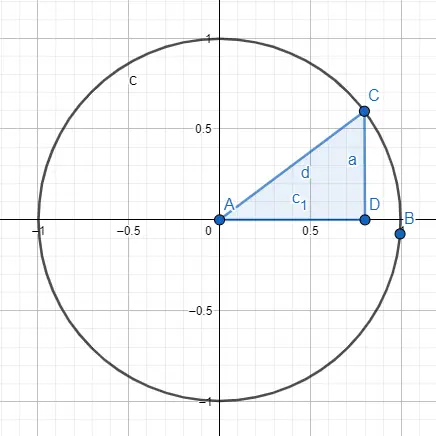
Bu görüntüye sahip olduğumuzda yarıçapın hipotenüse yani 1’e eşit olduğunu biliyoruz. Yani sinüs ve kosinüsü hesaplamak istiyorsak yarıçapın değerini ve diğer kenarların değerini kullanacağız. üçgen. Sinüsü hesaplamak için aşağıdaki hesaplamayı yapacağız: sin (A) = CD / AC = CD / yarıçap = CD / 1 = CD , dolayısıyla A’nın sinüsü a’dır. Öte yandan kosinüsü hesaplamak için şu hesaplamayı yapacağız: cos (A) = AD / AC = AD / yarıçap = AD / 1 = AD , dolayısıyla A’nın kosinüsü c1’dir.
İki şeyi akılda tutmak çok önemlidir. Birincisi, bu dairenin trigonometrik oranların incelenmesinde kullanılması, üçgenle çalışılabilecek açılardan daha büyük açılarla uğraşma ihtiyacından kaynaklanmaktadır. Örneğin 150 derecelik açı basit bir üçgende incelenemez çünkü çok büyüktür. Akılda tutulması gereken ikinci şey ise sinüs ve kosinüsün hiçbir zaman 1’den büyük ve -1’den küçük değerleri benimseyemeyeceğidir.
Trigonometrik oranların işareti
Daha önce de söylediğimiz gibi üçgenin bize sağladığı daha büyük açılarla uğraşmak için gonyometrik çevreyi kullanırız. Bunu yapmak için, dairenin içinde, daireyi bölen dört çeyrek daireden tam olarak birinde yer alan bir üçgeni temsil ediyoruz; aşağıdaki resimde temsil edilen dört çeyreği görebilirsiniz.
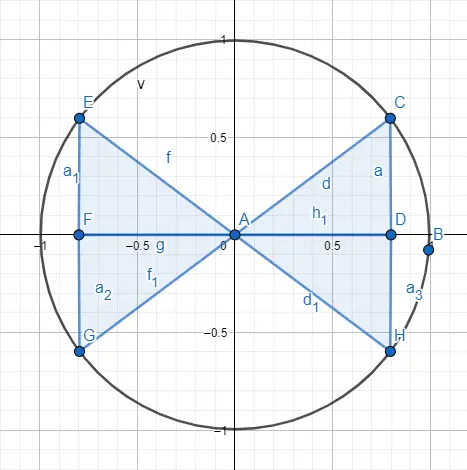
Yani aynı olan 30 derecelik bir açı ile 210 derecelik bir açıyı birbirinden ayırmak için üçgenin içindeki dağılımla ilgili , üçgenin bulunduğu çeyreğe göre işaret dağılımını kullanacağız. Aşağıda her çeyreğe karşılık gelen işaretleri ve çizilmiş bir örneği görebilirsiniz.
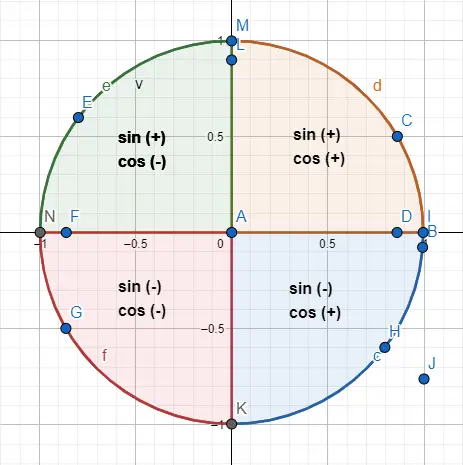
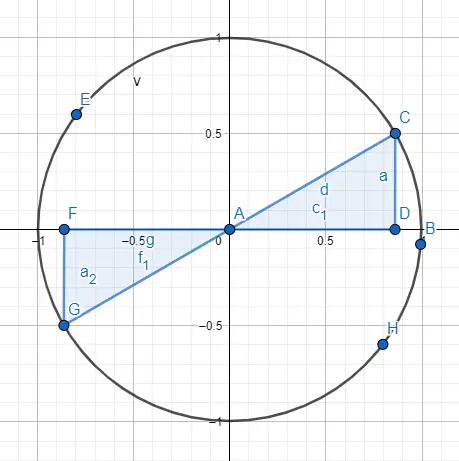
Örneğin, 30° ve 210° açıları aynı sayısal değeri paylaşır ancak sinüs ve kosinüsleri zıt işaretlere sahiptir. Yani: sin(30) = 1/2 ve cos(30) = √3/2, sin(210) = -1/2 ve cos(210) = -√3/2. Bu sonuca ulaşmak için çevredeki iki açıyı temsil ediyoruz (aşağıdaki resim) ve işaretlerin işaretlerini takip ediyoruz.
Son olarak, çevre sadece 360 derece olduğu için öyle görünmese de, 360 dereceden daha büyük açılara sahip olmanın nasıl mümkün olabileceği. Ancak 750° açı için çözmek istersek 0° ile 360° arasındaki bir açıya indirgeyebiliriz. Basitçe 750’yi 360’a böleriz ve kalan açı olur, 750° olursa 30° açı elde ederiz.
Çeyreğe bağlı olarak açı türleri
Farklı açılar arasında oranları hesaplamamızı sağlayan ilişkiler vardır. çembere ait tüm açıların trigonometrik değerleri. Bu nedenleri alalım ilk çeyreğe indirilmesi . Bu, ilk çeyreğe doğru belli bir açıdan sadeleştirme yapıp ardından ilgili işaretleri uygulamamız anlamına geliyor. Aşağıda açıklanan farklı prosedürleri bulacaksınız (çeyreklere bağlı olarak):
ilk çeyrek
Bu ilk çeyrekte (0° – 90°) sadece bize verilen açıyla trigonometrik oranı çözmemiz gerekiyor. Ve daha önce sembollerle ilgili açıkladığımız resme bakarsak, sinüs ve kosinüsün önünde pozitif var (elde ettiğimiz sonuç işaretten etkilenmeyecek).
İkinci çeyrekten birinciye azalma
İkinci çeyrekte (90° – 180°) bütünler açılarla uğraşıyoruz, bu da iki açının toplamının 180° olduğu anlamına gelir. Bu nedenle ikinci çeyrekten birinciye indirgeme yapmamız gerekiyor ve bunu 180 – α = β formülüyle yapıyoruz; burada α, birinci çeyreğin açısı ve β orijinal açıdır.
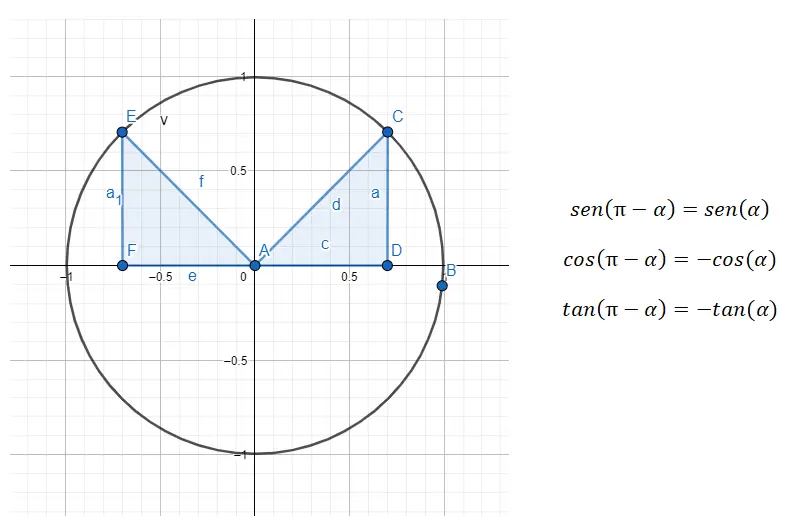
Örneğin bize 135° (ikinci çeyreğe ait) açı verilmişse, ilk önce bununla ilgili olan birinci çeyreğe ait açıyı bulmamız gerekir. Bu örnekte aradığımız açı (α) 45°, çünkü 180 – 45 = 135. Yani bu doğru olacaktır: sin (135) = sin (180 – 45) = sin (45), cos (135) ) = cos (180 – 45) = -cos (45) ve ten rengi (135) = tan rengi (180 – 45) = -tan rengi (45).
Üçüncü çeyreğin birinciye indirgenmesi
Üçüncü çeyrekte (180° – 270°) , birbirinden 80° farklı olan açılarla uğraşıyoruz, bu da açıların birbirlerinden 180° uzakta olduğu anlamına gelir. Yani üçüncü çeyrekten birinciye azaltmak istiyorsak, 180 + α = β formülünü kullanmamız gerekir; burada α, birinci çeyreğin açısıdır ve β , orijinal açıdır.
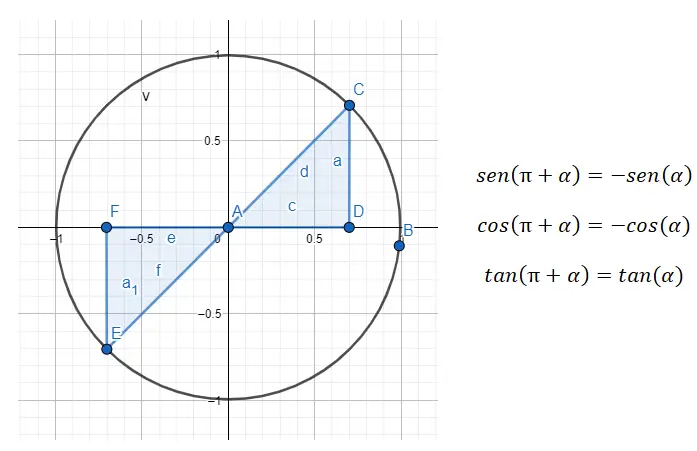
Örneğin bize 225° açı verilirse (ki bu üçüncü çeyreğe aittir), birinci çeyreğin ona karşılık gelen açısını bulmamız gerekir. 225° durumunda aradığımız açı (α) yine 45° olur, çünkü 180 + 45 = 225. Yani sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) ve tan (225) = tan (180 + 45) = tan (45) karşılanacaktır. ).
Dördüncü çeyreğin birinciye indirgenmesi
Dördüncü çeyrekte (270° – 360°) zıt açılarla ilgileniyoruz, bu, açıların sayısal olarak eşit ancak zıt işaretli olduğu anlamına gelir , 30° ve -30° gibi (360° – 30° = 330° olduğundan 330°’ye eşdeğerdir) . Karşıt açıların bir pozitif açı, bir negatif açı veya iki pozitif açı olarak yazılabileceğini unutmamak gerekir (az önce tartıştığımız örnekte farkı açıkladık).
Dolayısıyla, dördüncü çeyrekten birinciye bir indirgeme yapmak istiyorsak, 360 – α = β formülünü kullanmamız gerekir; burada α, birinci çeyreğin açısıdır ve β , orijinal açıdır.
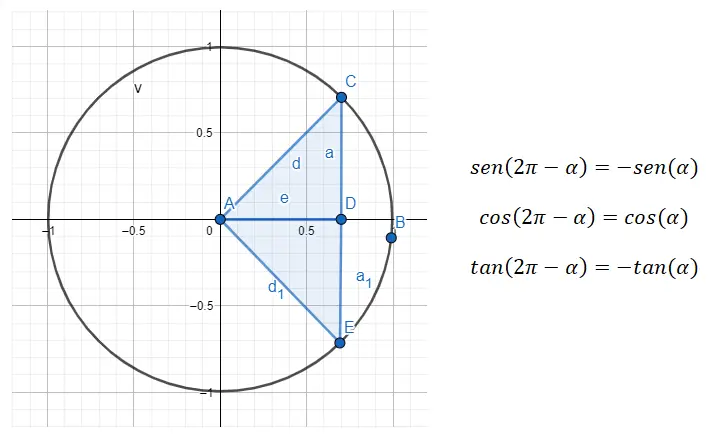
Örneğin bize 315° açısı (dördüncü çeyreğe ait) verilmişse, önce bununla ilgili olan birinci çeyreğin açısını bulmamız gerekir. Aradığımız açı (α) durumunda hala 45°’dir, çünkü 360 – 45 = 315. Yani sin (315) = sin (360 – 45) = -sin (45), cos ( 315) ) = cos (360 – 45) = cos (45) ve tan (315) = tan (360 – 45) = -tan (45). Sonuç olarak tüm çeyreklerin 45°’sinden elde edilen açıları gördük.
En önemli açıların trigonometrik oranları
Trigonometride en yaygın olan, dikkate değer açılar adı verilen bir dizi açı vardır. Trigonometrik oranlarınızı ezbere bilmeniz şiddetle tavsiye edilir. Bu nedenle aşağıda bu açıların ve türevlerinin trigonometrik oranlarını içeren bir tablo oluşturduk (aynı açılar ancak 90, 180 veya 270 derece farkla):
| Açı (°) | Açı (rad) | Göğüs | Kosinüs | Teğet |
| 0° | 0 rad | 0 | 1 | 0 |
| 30° | 1/6 rad | 1/2 | √3/2 | √3/3 |
| 45° | 1/4 πrad | √2/2 | √2/2 | 1 |
| 60° | 1/3 rad | √3/2 | 1/2 | √3 |
| 90° | 1/2πrad | 1 | 0 | ∞ |
| 120° | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135° | 3/4 πrad | √2/2 | -√2/2 | -1 |
| 150° | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180° | πrad | 0 | -1 | 0 |
| 225° | 5/4 πrad | -√2/2 | -√2/2 | 1 |
| 270° | 3/2πrad | -1 | 0 | ∞ |
| 315° | 7/4 πrad | -√2/2 | √2/2 | -1 |
Trigonometrik oranlar arasındaki ilişki
Farklı trigonometrik oranları ilişkilendirmenin birkaç yolu vardır. Bu ilişkilerden, trigonometrik özdeşlikler dediğimiz farklı trigonometrik fonksiyonlar arasında bir tür eşitlik elde ederiz. Bu tür kimlikler sayesinde herhangi bir diğerine dayalı bir oran hesaplayabiliyoruz. İfadenin kendisini destekleyen ilişki türüne göre sınıflandırılan birçok farklı trigonometrik kimlik türü olduğu unutulmamalıdır.
Trigonometrik Oranlar Çözülmüş Sorunlar
Daha sonra size bu makalede açıklanan tüm teoriyi uygulamaya koyabileceğiniz bir dizi alıştırma sunuyoruz. Unutmayın, herhangi bir zamanda takılıp kalırsanız veya sorularınız olursa, makaleyi tekrar okuyabilirsiniz ve ikinci bir okumada elbette her şeyi çok daha iyi anlayacaksınız. Bununla birlikte, pratik yapmaya başlayabilirsiniz:
1. Egzersiz
225° açısının altı trigonometrik oranını hesaplayın:
Şuna eşit olan açıyı (α) hesaplayarak başlayacağız: 180 + α = 225°, dolayısıyla α = 45°.
sin(225) = sin(180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
ten rengi(225) = ten rengi(180 + 45) = ten rengi(45) = 1
Alıştırma 2
120° açısının altı trigonometrik oranını hesaplayın:
Şuna eşit olan açıyı (α) hesaplayarak başlayacağız: 180 – α = 120°, dolayısıyla α = 60°.
sin(120) = sin(180 – 60) = sin(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
tan(120) = tan(180 – 60) = -tan(60) = -√3
Alıştırma 3
510° açısının altı trigonometrik oranını hesaplayın:
Başlamadan önce açı azaltma işlemini yapmalısınız: 510 / 360 = 1 dönüş ve kalan 150 açı. Daha sonra şuna eşit olan açıyı (α) hesaplıyoruz: 180 – α = 150, dolayısıyla α = 30°.
sin(150) = sin(180 – 30) = sin(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
tan(150) = tan(180 – 30) = -tan(30) = -√3/3