Üstel fonksiyonlar: özellikler, grafiksel gösterim, alıştırmalar,...

Bu sayfada üstel fonksiyonların ne olduğunu ve üstel bir fonksiyonun grafik üzerinde nasıl temsil edileceğini öğreneceksiniz. Ayrıca, onu tam olarak anlamanız için tüm özelliklerini ve birkaç örneğini göreceksiniz. Son olarak üstel fonksiyonlarla ilgili alıştırmalar ve adım adım çözülen problemlerle pratik yapabileceksiniz.

Üstel fonksiyon nedir?

Üstel fonksiyonun tanımı aşağıdaki gibidir:

Matematikte üstel fonksiyonlar , üssünde bağımsız değişken x olan fonksiyonlardır. Başka bir deyişle bunlar aşağıdaki gibidir:

$f(x)=a^x$

Altın

$a$

pozitif bir reel sayıdır ve 1’den farklıdır.

Üstel Fonksiyon Örnekleri

Aşağıdaki işlevler üstel işlevlere örnektir:

$f(x)=3^{x}$

$f(x)=4^{-x}$

$\displaystyle f(x)=\left( \frac{1}{2} \right)^x$

$f(x)=5^x$

Üstel fonksiyonların özellikleri

Üstel fonksiyonlar aşağıdaki özelliklere sahiptir:

Üstel bir fonksiyonun tanım kümesi gerçek sayılardan oluşur, başka bir deyişle herhangi bir x değeri için üstel bir fonksiyon mevcuttur.

$\text{Dom } f=\mathbff{R}$

Bununla birlikte, fonksiyon yalnızca pozitif değerler alır, dolayısıyla üstel bir fonksiyonun aralığı pozitif gerçek sayılardan oluşur.

$\text{Im } f= (0,+\infty)$

Her üstel fonksiyon hem sürekli hem de birebir fonksiyondur.

Eğer fonksiyon çevrilmezse herhangi bir üstel fonksiyon (0,1) noktasından geçer. Çünkü sıfır olarak değerlendirilen fonksiyon her zaman bir verir.

$f(0)=a^0=1$

Benzer şekilde üstel bir fonksiyonun x=1 noktasındaki değeri tabana eşittir.

$f(1)=a^1=a$

Eğer güç tabanı
$(a)$

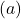
1’den büyükse üstel fonksiyon artıyor. Öte yandan eğer katsayı

$a$

0 ile 1 aralığında ise üstel fonksiyon azalmaktadır.

Genel olarak x ekseni, üstel bir fonksiyonun yatay bir asimptotudur.

Üstel fonksiyonun tersi logaritmik fonksiyondur. Bu nedenle, bir üstel fonksiyonun ve bir logaritmik fonksiyonun grafikleri, eğer her ikisi de aynı tabana sahipse, y=x doğrusuna göre simetriktir.

Üstel Bir Fonksiyonun Grafiği Nasıl Çizilir

Üstel fonksiyonların temsil edilmesi çok basittir. Şimdi bir örnek kullanarak üstel bir fonksiyonun grafiğini nasıl çizeceğimizi görelim.

Aşağıdaki üstel fonksiyonu bir grafik üzerinde çizin:

$f(x)=2^x$

Üstel fonksiyonlarda tanım kümesini hesaplamaya gerek yoktur çünkü bunların hepsi her zaman gerçek sayılar olacaktır:

$\text{Dom } f = \mathbb{R}$

Bu nedenle değerler tablosunu hazırlamak yeterlidir. Bu tür fonksiyonlar bir noktadan diğerine çok fazla değiştiği için 5 puan hesaplayacağız. Ancak ne kadar çok nokta hesaplarsak fonksiyonun temsili o kadar kesin olur.

$x= 0 \ \longrightarrow \ f(0)=2^0= 1$

$x= 1 \ \longrightarrow \ f(1)=2^1= 2$

$x= 2 \ \longrightarrow \ f(2)=2^2= 4$

$x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5$

$x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}$

Elle hesaplamak karmaşık olduğundan, değer tablosundaki noktaları bulmak için bir hesap makinesi kullanmanızı öneririz.

Şimdi noktaları bir grafik üzerinde temsil ediyoruz :

Ve son olarak noktaları birleştirip fonksiyonu genişletiyoruz:

üstel bir fonksiyonun nasıl temsil edileceği veya grafiğinin nasıl çizileceği

Sağdaki fonksiyonun sonsuza kadar büyümeye devam ettiğine dikkat edin.

Buna karşılık soldaki fonksiyon azalır ama hiçbir zaman 0’a ulaşmaz. Çok yaklaşsa da hiç dokunmaz. Bu, y=0 çizgisinin (x ekseni) yatay bir asimptot olduğu anlamına gelir.

Üstel fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki üstel fonksiyonun grafiğini çizin:

$f(x)= 2^x+1$

Çözümü görün

Bu üstel bir fonksiyondur, dolayısıyla onu temsil etmek için x değişkenine değerler veren bir değerler tablosu oluşturmalısınız:

$x= 0 \ \longrightarrow \ f(0)= 2^0+1=2$

$x= 1 \ \longrightarrow \ f(1)= 2^1+1=3$

$x= 2 \ \longrightarrow \ f(2)= 2^2+1=5$

$x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5$

$x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}$

Değer tablosunu elde ettikten sonra, elde edilen noktaları grafikte çizeriz ve fonksiyonun grafiğini çizeriz:

üstel fonksiyonların adım adım çözüldüğü egzersiz

Sağdaki fonksiyonun sonsuza kadar büyümeye devam ettiğine dikkat edin. Sol tarafta ise fonksiyon azalır ama hiçbir zaman 1’i aşmaz. Aslında fonksiyonun sağında y=1 yatay asimptotu vardır.

Bu durumda yatay asimptot OX ekseni yerine y=1’dedir çünkü fonksiyona doğru bir birim yukarıya doğru dikey öteleme yapılmıştır.

Alıştırma 2

Aşağıdaki üstel fonksiyonu bir grafik üzerinde çizin:

$\displaystyle f(x)= \left(\frac{1}{3}\right)^x$

Çözümü görün

Bu üstel bir fonksiyondur, dolayısıyla onu grafiksel olarak temsil etmek için x değişkenine değerler veren bir değerler tablosu oluşturmalısınız:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}$

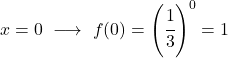
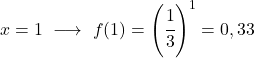
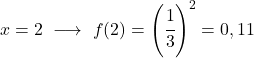
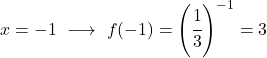
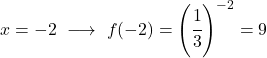
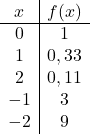
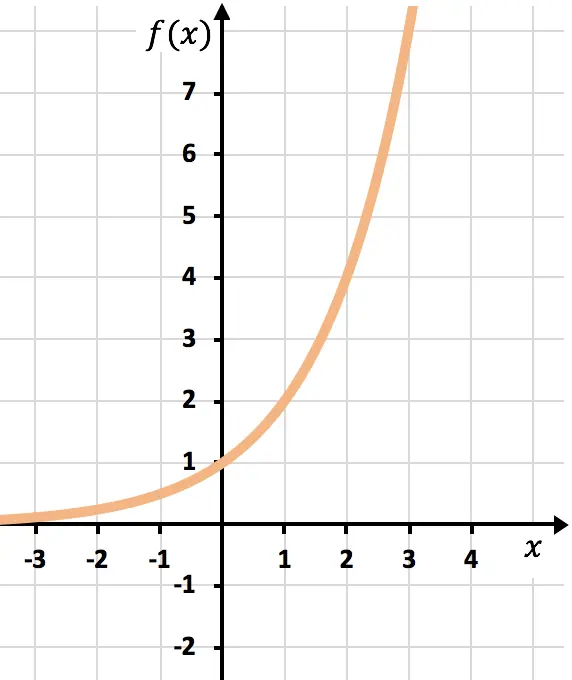
Değer tablosunu elde ettikten sonra hesaplanan noktaları grafik üzerinde çizer ve fonksiyonu çizeriz:

Soldaki fonksiyonun sonsuza kadar büyümeye devam ettiğine dikkat edin. Öte yandan sağda fonksiyon azalır ama asla 0’ı aşmaz. Aslında fonksiyonun y=0’da (X ekseni) yatay bir asimptotu vardır.

Alıştırma 3

Aşağıdaki üstel fonksiyonu bir grafik üzerinde çizin:

$\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3$

Çözümü görün

Bu üstel bir fonksiyondur, dolayısıyla onu çizmek için fonksiyonu birkaç noktada değerlendiren bir değerler tablosu oluşturmanız gerekir:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}$

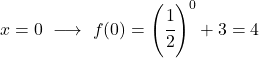
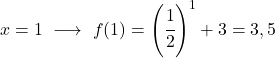
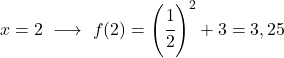
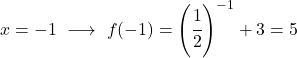
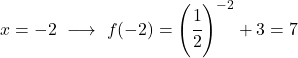
Son olarak elde edilen noktaları grafikte temsil ediyoruz ve fonksiyonu çiziyoruz:

Soldaki fonksiyonun sınırsız bir şekilde sonsuza kadar büyüdüğünü unutmayın. Sağ tarafta ise fonksiyon azalıyor ama hiçbir zaman 3’ü geçmiyor. Aslında fonksiyonun y=3 noktasında yatay bir asimptotu var.

Bu durumda yatay asimptot X ekseni yerine y=3’tedir çünkü fonksiyon dikey olarak üç birim yukarı taşınmıştır.

Alıştırma 4

Üstel fonksiyonlarla ilgili aşağıdaki problemi çözün.

Değerini belirleyin
$k$

böylece bir sonraki üstel fonksiyon (2.8) noktasından geçer.

$f(x)=k\cdot 2^x$

Çözümü görün

Fonksiyonun (2,8) noktasından geçmesi gerekir, dolayısıyla k sabitinin değerini bulmak için noktanın x ve f(x) değerlerini fonksiyonda değiştirebiliriz :

$f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2$

Ve şimdi ortaya çıkan denklemi çözüyoruz:

$8 = k \cdot 2^2$

$8 = k \cdot 4$

$\cfrac{8}{4} = k$

$\bm{ 2 = k}$

Alıştırma 5

Üstel fonksiyonlarla ilgili aşağıdaki problemi çözün.

Bir termit popülasyonu aşağıdaki fonksiyona göre çoğalır:

$f(t)=3^{t+1}$

Altın

$f(t)$

termitlerin sayısı ve

$t$

aylar geçti zaman.

1 yıl sonra kaç tane termit olacak?

Çözümü görün

Bir yılda oluşacak termit sayısını hesaplamak için geçen süreyi (1 yıl) fonksiyona yazmanız yeterlidir. Ancak t fonksiyonu yıllar değil de geçen aylar olduğundan, bir yılda 12 ay olduğundan t =12 koymalıyız:

$f(t)=3^{t+1}$

$f(12)=3^{12+1}$

$f(12)=3^{13}$

Hesap makinesiyle çözüyoruz:

$f(12)= 1594323$

Yani bir yıl sonra 1.594.323 termit olacak.

Üstel fonksiyon nedir?

Üstel Fonksiyon Örnekleri

Üstel fonksiyonların özellikleri

Üstel Bir Fonksiyonun Grafiği Nasıl Çizilir

Üstel fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et