Magic Squares , hesaplama becerilerimizi eğlenceli ve heyecan verici bir şekilde geliştiren bir matematik bulmaca oyunudur. Bu nedenle genç öğrencilere matematik öğretmek için en iyi kaynaklardan biridir.
Sihirli dizi nedir ve nasıl çözülür?
Sihirli kare, içine tamsayıların yazıldığı, farklı kutulardan oluşan bir tür tablo veya matristir. Ancak hiçbir durumda kurulamazlar; bir dizi kurala uyulmalıdır:
- Tüm sihirli toplamlar (herhangi bir yatay, dikey veya çapraz çizginin tüm değerlerinin toplamı) her zaman sihirli sabite eşdeğer değeri vermelidir (tek bir değerdir).
- Hiçbir sayı iki kez tekrarlanamaz.
- Yalnızca ardışık sayıları (örneğin, 1’den 9’a kadar) veya belirli bir seriyi izleyen sayıları kullanabilirsiniz; örneğin: tek sayılar, 5’in katları ve diğerleri.
Ayrıca kareleri yapılarına göre farklı sınıflandırmalar yapabileceğimizi de vurgulamakta fayda var. Birincisi, bir satır veya sütundaki hücre sayısına eşdeğer olan karenin derecesine göredir. İkincisi ise tablonun derecesine göredir ( çift sayı veya tek sayı). Bu ayrımlardan tüm kareleri farklı kategoriler halinde düzenleyebiliriz, ancak bunu daha sonra detaylandıracağız.
Sihirli kareler nasıl çözülür?
Bu matematik oyununu çözmek için iki farklı yöntem kullanabiliriz: geometriyi kullanın veya sihirli sabiti hesaplayın. Her iki prosedür de eşit derecede geçerlidir, ancak biri sonuca daha hızlı ulaşmanızı sağlarken diğeri daha fazla zaman ve akıl yürütme gerektirir. Daha sonra her iki yöntemi de açıklayacağız, böylece tercih ettiğiniz yöntemi seçebilir ve her duruma daha iyi uyum sağlayabilirsiniz.
Sihirli karelerin formülü nedir?
İlk yöntem, sihirli sabitin hesaplanmasından oluşur ve bunun için şu formülü kullanmamız gerekir: n(n 2 +1)/2, burada n, karenin derecesidir. Ve bu değere sahip olduğumuzda geriye kalan tek şey, tüm karenin sihirli toplamlarını sabite eşitlememizi sağlayan farklı sayı kombinasyonlarını denemektir. Başka bir deyişle, tüm resmin dengeli olması için toplamı sabitin değerine eşit olan sayı kombinasyonları oluşturmamız gerekiyor.
Sihirli kareler geometri kullanılarak nasıl çözülür?
İkincisi, sihirli kareleri geometri kullanarak çözebiliriz. Ancak bu yöntemin çok basit olduğunu ve tamamen yöntemsel olduğu için hesaplama becerilerinizi geliştirmenizi gerektirmediğini de belirtmek gerekir. Bununla birlikte, hem çift sıralı kareleri hem de tek sıralı kareleri çözme prosedürünü açıklayacağız.
Tek sayılarla sihirli kareler nasıl çözülür?
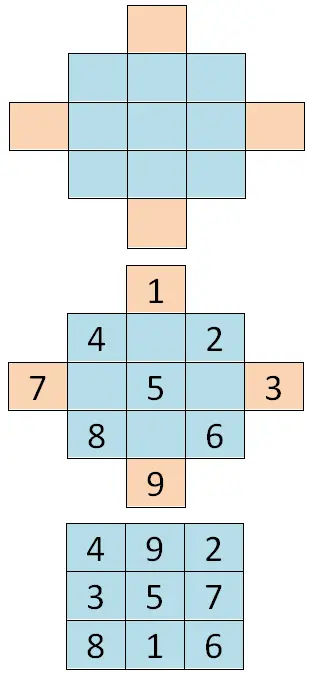
Bu ilk durumu çözmek için, bir çeşit elmas elde etmek için ilk tabloya hücreler eklemelisiniz. Daha sonra serinin ilk rakamından başlayarak ardışık tüm sayıları yazmalıyız (bizim durumumuzda 1) ve baklavanın köşegenlerini takip edeceğiz. Son olarak rakamı “ikiye katlamamız” gerekiyor, bu nedenle dış hücrelerin değerleri karşı tarafa gidiyor. Böylece dikey eksenin dış hücreleri kesişir, o zaman aynı şey yatay eksenin hücreleri için de olur, aşağıda bir örnek görebilirsiniz:
Eşit sıradaki sihirli kareler nasıl çözülür?
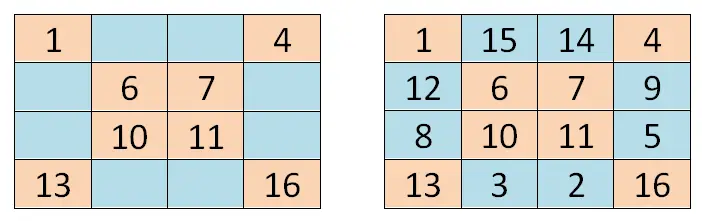
Eşit düzendeki sihirli bir kareyi (çift sayıda satır ve sütuna sahip sihirli kareler) çözmek için, öncekinden biraz farklı ama aynı zamanda geometriye dayanan bir yönteme başvurabiliriz. Sol üst köşeye serinin ilk sayısını (bizim durumumuzda 1) yazarak başlayacağız. Daha sonra iki ana köşegeni geçerek her kutunun konumuna karşılık gelen değerleri yazacağız.
İki ana köşegeni yazdıktan sonra sağ alt köşeden başlayarak ilk boş kutuya (bizim durumumuzda kutu 15) kendimizi yerleştirmemiz gerekecek. Orada serinin ikinci değerini yazacağız ve kalan değerleri sırasıyla (küçükten büyüğe) hücreleri sağdan sola ve aşağıdan yukarıya doğru tamamlayarak yazacağız. Daha açık hale getirmek için, aşağıda size gösterdiğimiz görsele göre kendinizi yönlendirebilirsiniz:
Sihirli kareler nasıl oluşturulur?
Kendimiz sihirli kareler inşa etmek için çeşitli prosedürleri takip edebiliriz, bunlardan ikisini vurgulayacağız. Her birinin farklı türde kareler oluşturmak için kullanılacağını unutmayın; bu nedenle, oluşturmak istediğiniz kareye bağlı olarak yöntemi dikkatli bir şekilde seçmeniz gerekecektir:
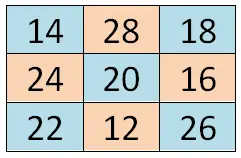
Siyam yöntemi
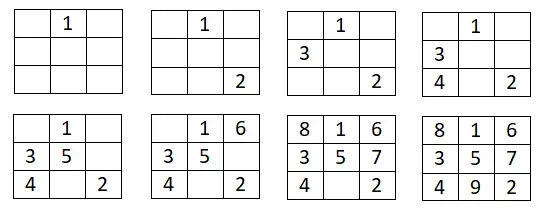
Bu ilk yöntem oldukça basittir ve özellikle her boyutta tek sihirli kareler oluşturmamıza yardımcı olur. İzlenecek prosedür çok basit, temel olarak serinin ilk sayısını ilk satırın ortasındaki kutuya yazacağız. Oradan, seçtiğimiz aritmetik ilerlemeye göre sırayla geri döneceğiz ve bir sonraki sayıyı yukarıya ve sağa yazacağız. Ancak bu konum çizilen karenin dışındaysa son satır veya sütuna geçmek zorunda kalacağız. Ve eğer tam kare elde edersek son girdiğimiz sayı karesinden bir kare aşağı inip aynı şekilde devam edeceğiz.
Aşağıda 3×3 örneğini görebilirsiniz:
Strachey’nin sihirli kareler yöntemi
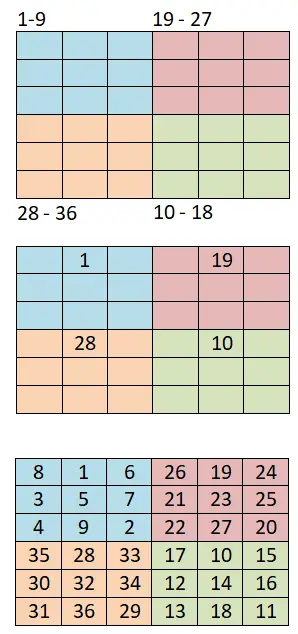
4k + 2 çift düzeyinde sihirli kareler oluşturmak için, bir önceki yöntemi (Siyam yöntemi) temel alan ve aynı zamanda çok basit olan bu diğer yöntemi kullanacağız. Aşağıda izlenecek adımları ve 6×6 sihirli karenin çalışılmış bir örneğini görebilirsiniz:
- Daha küçük çeyreklere bölme: Yapmamız gereken ilk şey, tahtayı daha küçük karelere bölmek, örneğin 6×6’lık bir tahtamız varsa, 3×3 karelerden oluşan dört eşit çeyrek yapmamız gerekecek.
- Siyam yöntemini kullanın: o zaman her küçük çeyreğe bir sayı aralığı atayacağız, örneğin diziye 1 ile başlarsak aralıklar şöyle olacaktır: 1-9 (birinci), 10-18 (dördüncü), 19-27 (ikinci) ve 28-36 (üçüncü).
Sihirli kareler için Conway’in LUX yöntemi
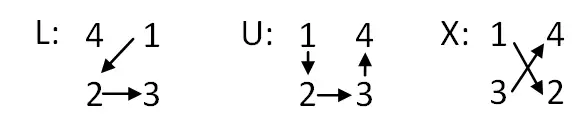
n’nin bir doğal sayı olduğu 4n + 2 düzeyinde sihirli kareler oluşturmak istediğimizde ikinci sistemi kullanacağız. Bu tarzda kareler oluşturmak için izleyeceğimiz prosedür şu şekildedir:
- Tablo veya matris oluşturma: n’nin bir doğal sayı olduğu 2n + 1 dereceli bir matris oluşturarak başlayacağız. Bununla masayı tasarlayabileceğiz ve derecesini aklımızda tutarak tasarıma başlayacağız.
- Harflerin konumlandırılması: Tablo oluşturulduktan sonra yukarıdan aşağıya yazmanız gerekecek: n + 1 satır L, 1 satır U ve n – 1 satır X. Daha sonra U’yu değiştirmeniz gerekecek. ortada, L üstte.
- Harfleri sayısal değerlerle değiştirin: Şimdi harfleri ardışık dört sayıdan oluşan gruplarla değiştirmemiz gerekecek. Mektuba bağlı olarak sayılara şu veya bu sırayı vereceğiz. Aşağıda açıklanmıştır:
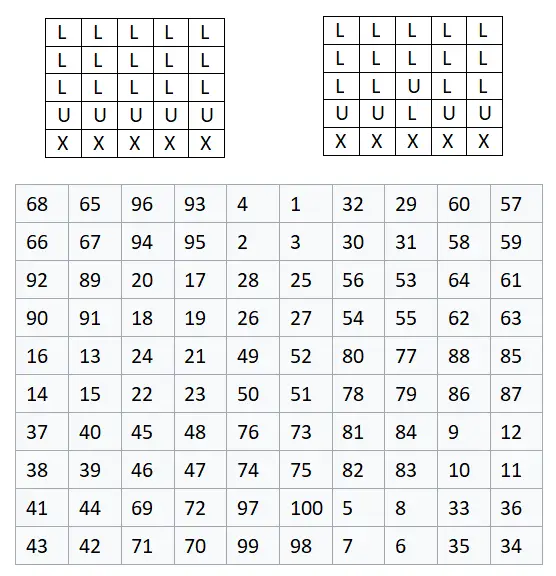
5×5’lik bir matris oluşturarak başlayacağız, yani n = 2, çünkü: 2n + 1 = 2 · 2 + 1 = 5. Bu, matrisin 10×10 boyutuna sahip olacağı anlamına gelir, çünkü aşağıdaki gibi Daha önce de söylediğimiz gibi, içerisinde harf bulunan her hücre dört rakamdan oluşan bir gruba, yani 2×2’lik bir matrise eşdeğerdir. Aşağıda, her harfi resimde gösterilen sıraya göre dört sayıdan oluşan bir grupla değiştirdiğimiz tamamlanmış örneği görebilirsiniz:
sihirli kareler egzersizleri
Daha sonra size bazı tamamlanmamış sihirli kareler sunuyoruz ve bu yazıda anlattığımız kavramlar sayesinde onları kendiniz doldurmanız gerekecek. Öğretilen yöntemlerden herhangi birini kullanabileceğinizi unutmayın. Ek olarak, bildirimde yer alacak olsa da 1’in serideki ilk sayı olmayabileceğini dikkate almanız gerekir. Alıştırmalardan birini bitirdiğinizde çözümü ifadenin altında görebileceksiniz.
3×3 sihirli kare
Yalnızca tek sayılardan oluşan 3×3’lük bir sihirli kare oluşturun:
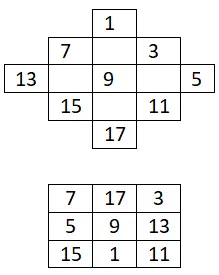
4×4 sihirli kare
Aşağıdaki 4×4 sihirli kareyi tamamlayın:
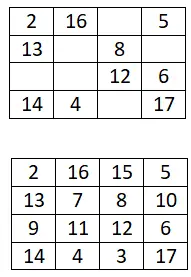
5×5 sihirli kare
Aşağıdaki 5×5 sihirli kareyi tamamlayın:
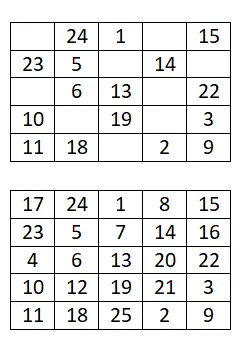
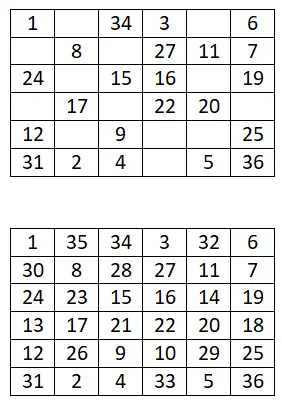
6×6 sihirli kare
Aşağıdaki 6×6 sihirli kareyi tamamlayın: