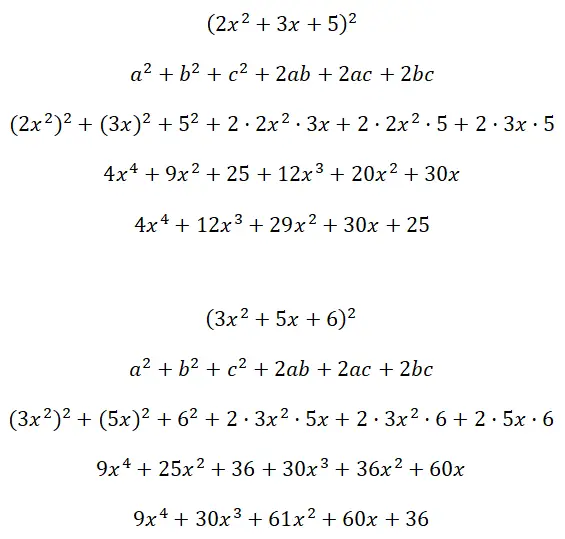Dikkat çekici ürünler

Dikkat çekici ürünler veya dikkat çekici kimlikler nelerdir?

Dikkat çekici ürünler veya dikkate değer eşitlikler olarak da adlandırılan dikkat çekici özdeşlikler , polinomların çarpımlarının ve bölümlerinin daha hızlı çözülmesini sağlayan matematiksel kaynaklardır. Kimlik kelimesinin de belirttiği gibi bunlar, bu işlemleri çözmemize gerek kalmadan hesaplamamızı sağlayan eşitliklerdir. Bu ifadenin (her zaman karşılanan) sabit kurallara uyduğunu bildiğimizden, sonucu kontrol etmeye gerek kalmadan elde edebiliriz.

Dikkate değer bir kimlik ne zaman kullanılmalı?

Bu kimlikler esas olarak cebir alanında kullanılır ve temel işlevleri, tüm işlemi kendisi çözmek zorunda kalmadan belirli bir polinomun çözümünü hızlandırmaktır. Buradan yazı boyunca yorumlayacağımız önemli ürünlerin formüllerini alıyoruz. Ve son olarak formülleri tam karelere,faktör polinomlarına veya başka herhangi bir hesaplama türüne uygulayabiliriz.

Dikkat çekici bir ürünü adım adım nasıl çözebilirim?

Dikkate değer kimlikleri çözmek için çok basit bir prosedür izlemeniz gerekir ve bu da oldukça mantıklıdır:

• Dikkate değer kimlik türünü belirleyin: İlk adım, operasyon türünü tanımlamaktır: dikkate değer bir ürün veya dikkate değer bir bölüm. Ayrıca ne tür bir formül uygulamanız gerektiğini de açıklığa kavuşturmalısınız, ancak bunu daha sonra farklı önemli kimlik türlerini açıkladıktan sonra anlayacaksınız.
• Formülü uygulayın: Hangi formülü uygulamanız gerektiğini öğrendikten sonra sıra hesaplamalara gelir. Kimliğin türüne bağlı olarak az ya da çok karmaşık işlemleri çözmeniz gerekecek ve çoğu durumda bu hesaplamalar en az bir bilinmeyen içeren terimlerden oluşacaktır.
• İfadeyi sadeleştirin: Son olarak sonuca ulaştığınızda sadeleştirmeniz gerekir. Bu adımda, benzer terimleri gruplamanız ve bunları iyi yapılandırılmış bir sonuç polinomu oluşturacak şekilde sıralamanız gerekir. Bu adımın diğerleri kadar önemli olduğuna dikkat edilmelidir, aksi takdirde alıştırma eksik kalacaktır.

Önemli kimliklerin veya ana önemli ürünlerin formülleri

Aşağıda önemli kimliklere karşılık gelen tüm formülleri bulacaksınız. Her bir vakanın teorik açıklamasına ek olarak, tüm kavramları daha iyi anlayacağınız bazı dikkate değer çözümlenmiş ürün örnekleri de bulunmaktadır. Bu ilk bölümde yalnızca en önemli kimlikleri bulacağınızı belirtmekte fayda var. Ancak bu makaleyi okuyarak, üç terimlilerden yapılanlar gibi daha karmaşık dikkate değer ürünlerin nasıl geliştirileceğini öğreneceksiniz.

bir toplamın karesi

İlk durum cebir dünyasında çok yaygın bir polinom ifadesi olan toplamın karesiyle ilgilidir. Bu, (a + b) ² şeklinde yazılı olarak bulunabilir; bu da şuna eşdeğerdir: (a + b) · (a + b). Bu nedenle polinom çarpımı kullanılarak çözülebileceğini biliyoruz. Ancak dikkate değer kimlikler sayesinde şu formülü kullanarak zamandan tasarruf edebiliriz: (a + b) ² = a ² + 2ab + b ² . Daha sonra size az önce gördüğümüz formülün gösterimini göstereceğiz, böylece bu formülün nereden geldiğini ve nasıl kullanıldığını anlayabilirsiniz:

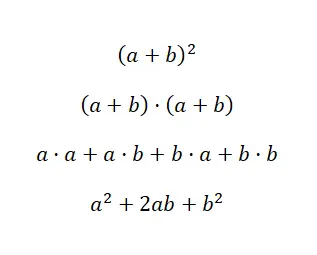
Görüldüğü gibi doğrulamayı daha önce yorum yaptığımız polinomların çarpımını kullanarak gerçekleştirdik. Ve mutlak bir kesinlikle söyleyebiliriz ki, ortaya çıkan formülü ezbere biliyorsanız, değerlerin basit bir şekilde değiştirilmesiyle sonucu daha hızlı alabilirsiniz. Bu çok yararlı bir matematiksel kavramdır. Artık bir toplamın karesinin nasıl çalıştığını bildiğinize göre size somut bir örnek göstereceğiz:

Bir toplamın karesi örneği

Dikkate değer kimliği hesaplayın (2x + 4) ² :

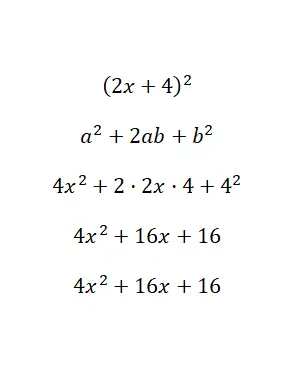
Temel olarak binomun değerlerini formülün harfleriyle ilişkilendirdik ve şunu çözdük: a = 2x ve b = 4. Son olarak tüm hesaplamaları çözdükten sonra 4x ² + 16x + 16 polinomunu elde ediyoruz; orijinaline eşdeğerdir . Bu örnekte, indirgenmiş bir polinomdan genişletilmiş bir polinom (standart biçimde) elde ettik.

bir çıkarmanın karesi

Bir başka çok yaygın ifade de çıkarmanın karesidir ; bu, toplamanın karesine çok benzer, yalnızca bir işaret değişir. O halde binomun yapısı şuna eşdeğerdir: (a – b) ² ve onu açarsak şunu elde ederiz: (a – b) · (a – b). Önceki durumda olduğu gibi, bu, polinomların çarpımından hesaplanabilir, ancak aynı zamanda çözümü kolaylaştıran bir formüle de sahiptir: a ² – 2ab +b ² . Aşağıda bunun ampirik kanıtını bulabilirsiniz:

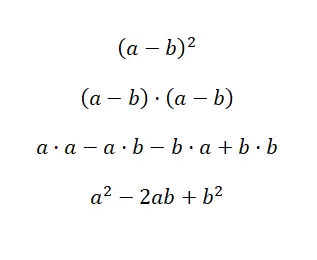
Bir farkın karesini çözmeyi kolaylaştırmak için, karenin toplamı için kullandığımız formülün aynısını kullanabiliriz, ancak ilk işareti negatiftir . Bu minimum değişiklik, ifadenin bir pozitif terim ve bir negatif terimden oluşan binomlara uyarlanmasına olanak tanır ve bu da çıkarma işlemleri için faydalıdır. Şimdi size çözülmüş bir örnek göstereceğiz:

Bir çıkarma işleminin karesi örneği

Dikkate değer kimliği hesaplayın (x – 3) ² :

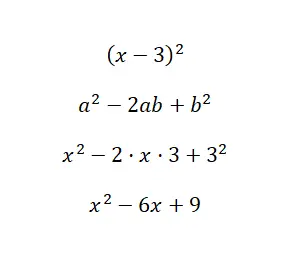
Örnek çözümde görebileceğiniz gibi, binomumuzun değerlerini a = x ve b = 3 formülünde yerine koyduk. Bu nedenle, daha önce açıkladığımız formülü kullanarak sadece değiştirme işlemini yaptık ve bazı çok basit işlemleri yaptık. hesaplamalar. Bu da bu ifadeyle bir farkın karesinin ne kadar kolay hesaplanabileceğini görmemizi sağlar.

Kareler farkı veya farka göre toplam

Dikkate değer çarpımların üçüncü durumuna kareler farkı denir; bu, pozitif bir binom ile negatif bir binomun çarpımından oluşur. Bu stildeki bir ifade şu yapıya sahiptir: (a + b) · (a – b), yani bu çarpımı genişletirsek hesaplamayı kolaylaştıran formülü elde ederiz: a ² – b ² . Gördüğünüz gibi bu çok basit bir formül, ancak onu tam olarak anlamak için tüm hesaplamaları geliştirmeniz gerekiyor:

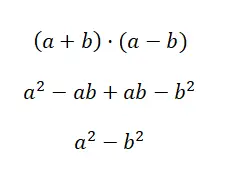
Farklara göre toplam örneği

Dikkate değer kimliği hesaplayın (x + 1) · (x – 4):

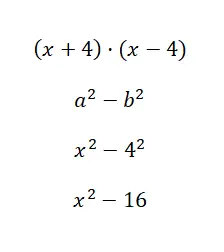
Bu durumda sayısal hesaplama çok kolay, aslında sadece bir kuvveti çözmemiz gerekiyordu. Her ne kadar bu formülün yalnızca binomların aynı ana terime ve aynı bağımsız terime sahip olduğu, ancak işareti değiştirilmiş olduğu durumlarda uygulanabilir olduğu doğru olsa da. Yani bu kimlik önemli ama en çok kullanacağınız kimlik bu değil.

Ortak terimli iki binomun çarpımı

Bu dördüncü durumda, yapıda ufak bir değişiklik olsa da kendimizi bir öncekine çok benzer bir durumla karşı karşıya buluyoruz. Size gösterdiğimiz farkı gözlemleyin: (x + a) · (x + b) ve (a + b) · (a – b). Hala çok net göremiyorsanız şu örneği inceleyin: (x + 4) · (x + 5) ve (x + 4) · (x – 4). İlk durumda ( iki ortak terimli binomun çarpımı ) yalnızca bir ortak terim bulunurken, ikinci durumda (farkın toplamı) iki terim ortaktır, ancak bağımsız terimin ters işareti vardır. Bununla birlikte, hangi formülle hareket edebileceğimize bakalım:

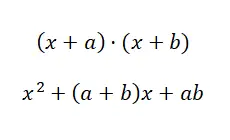
Ortak terimli iki binomun çarpımına örnek

Dikkate değer çarpımı (x + 2) · (x + 3) bulun:

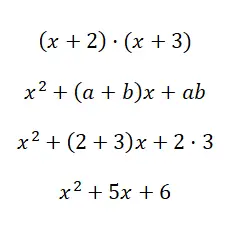
x ² + (a + b)x + ab formülünü kullanarak iki binomun çarpımından elde edilen ikinci derece polinomu hesaplayabiliriz. Bu örnek sayesinde, anlattığımız son iki durum arasındaki farkı anlamış olduğunuzu umuyoruz, çünkü bazen bunları ayırt etmek zor olabilir.

bir üçlünün karesi

Bir trinomialin karesini hesaplamaya çalıştığımızda karşımıza hayatımızı kolaylaştıran dikkat çekici bir ürün çıkıyor. Bu ifade şu şekilde temsil edilir: (a + b + c) ² ve eşdeğer çarpım şu şekildedir: a ² + b ² + c ² + 2ab + 2ac + 2bc. Bunun pozitif trinomial durumunda geçerli olduğunu belirtmek gerekir, ancak katsayılardan biri negatifse formüle negatif değeri yazmanız yeterlidir. Aşağıda formülün gösterimi verilmiştir:

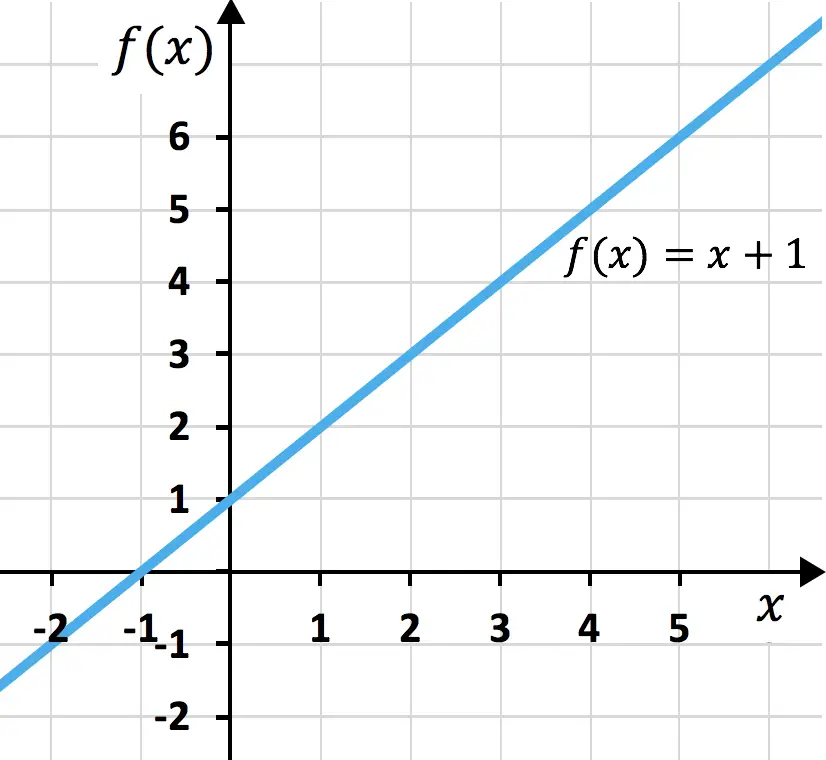
Üç terimlinin karesi örneği

Dikkate değer özdeşliği (2x + 1 + x ² ) ² hesaplayın:

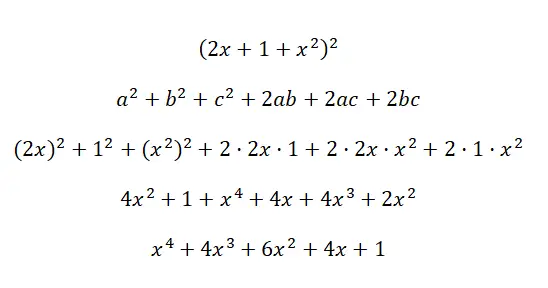
Dikkat çekici kimlik formülleri veya dikkat çekici küplü ürünler

Artık dikkate değer temel özdeşlikleri açıkladığımıza göre, binomların küpüyle başlayarak türevlerine bakacağız. Bu tarzdaki dikkate değer ürünleri hesaplamak için, biraz daha karmaşık olan ancak daha önce tartıştığımız formüllere benzer bir yapı izleyen formüllere başvurmamız gerekecek.

binom küp

Binomun küpü şöyle yazılır: (a + b) ³ ve (a – b) ³ , bu ifade aşağıdaki formüle eşdeğerdir: (a ³ + 3a ² b + 3ab ² + b ³ ) ve (a ³ – 3a ² b + 3ab ² – b ³ ). Bu iki duruma toplamın küpü ve çıkarmanın küpü denir çünkü bunlar küp binomdur. Aşağıda her vakanın çok ayrıntılı bir gösterimini bulacaksınız:

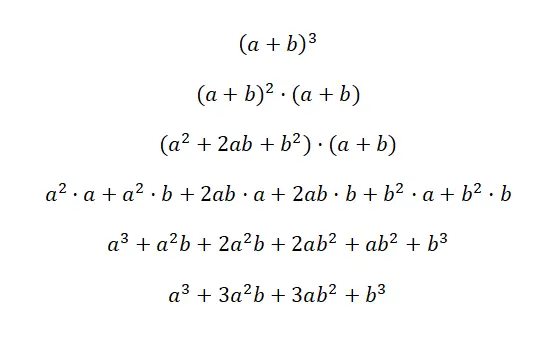
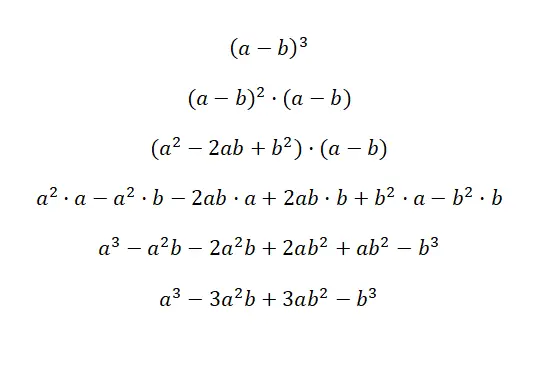
Bu ilk kanıtı anlamanın anahtarı, (a + b) ^3’ün şuna eşdeğer olduğunu anlamaktır: (a + b) ² · (a + b). Bu şekilde diğer çarpanı çarpmak için daha önce açıkladığımız toplamın karesi formülünü kullanıyoruz. Daha sonra ifadeyi basitleştiririz ve karşılık gelen dikkate değer özdeşliği elde ederiz: a ³ + 3a ² b + 3ab ² + b ³ . İkinci örnekte de aynı şey oluyor ama işaret değişikliğiyle.

Binom küp örneği

Dikkate değer özdeşliği çözün (x + 3) ³ :

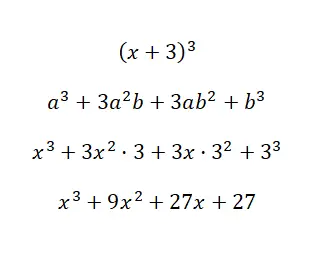
Az önce tartıştığımız formülü kullanarak polinomu şunu hesaba katarak hesaplayabiliriz: a = xyb = 3. Gördüğünüz gibi prosedür çok basit ve hesaplamada pek fazla komplikasyon yok, çünkü elimizde formül var. . Aksi takdirde bu kadar çok çarpma işlemi yapmak oldukça sıkıcı olacaktır.

Küplerin toplamı ve küplerin farkı

Bir de bir öncekiyle kolayca karıştırılabilecek başka bir durum var. Her iki durum farklı yazılsa da eşdeğer değildir. Küplerin toplamına veya farkına eşdeğer ifade şu şekildedir: a ³ + b ³ , oysa önceki durumda bahsettiğimiz: (a + b) ³ . Gördüğünüz gibi ifadenin yapısında yadsınamaz bir benzerlik var ama gerçekte iş hesaplamayı geliştirmeye gelince, bunlar tamamen farklı iki durum:

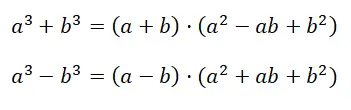
Formülün gösteriminde , ilk polinomun çarpanlara ayrılmasını elde ediyoruz, tam olarak başlangıç binomundan bir binomun bir trinomial çarpımına gidiyoruz. Elde edilen (a + b) · (a ² – ab + b ² ) sonucu hesaplamayı hiç kolaylaştırmıyor gibi görünüyor, ancak gerçekte polinomu çarpanlara ayırarak anlaşılması çok kolay bir ifade elde ediyoruz.

Küp toplamı örneği

Dikkate değer çarpım x ³ + 27’yi hesaplayın:

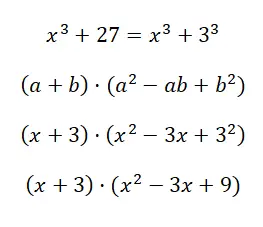
Bu durumda elde ettiğimiz sonuç oldukça uzundur çünkü daha fazla basitleştirilemez. Ancak bu ifadeye ulaşmanız normaldir, aslında bu durumlarda bu örnekte olduğu gibi ancak bir binomun bir trinomial ile çarpımına eşdeğer yapıda bir sonuç elde edebilirsiniz.

üç terimli küp

Bir üç terimlinin küpü şöyle yazılır: (a + b + c) ³ , bu da üç özdeş üç terimliyi çarpmak anlamına gelir, ancak üs olmadan: (a + b + c) · (a + b + c) · (a + b + c). Formül oldukça mantıklı olmasına ve polinomların karşılık gelen çarpımlarını gerçekleştirdiğinizde hepsiyle aynı şekilde elde edilmesine rağmen, var olan en karmaşık dikkate değer üründür. Aşağıda bu dikkat çekici kimliğin formülünün kanıtını bulacaksınız:

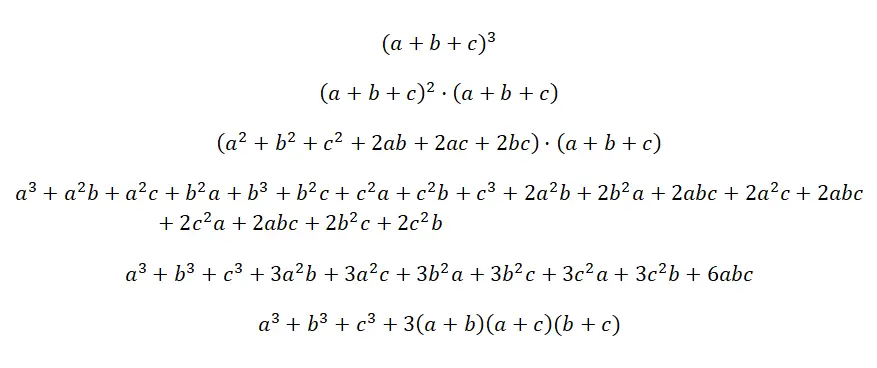
Üç terimli küp örneği

Aşağıdaki trinomiyal küpü (x ² + 3x – 4) ³ çözün:

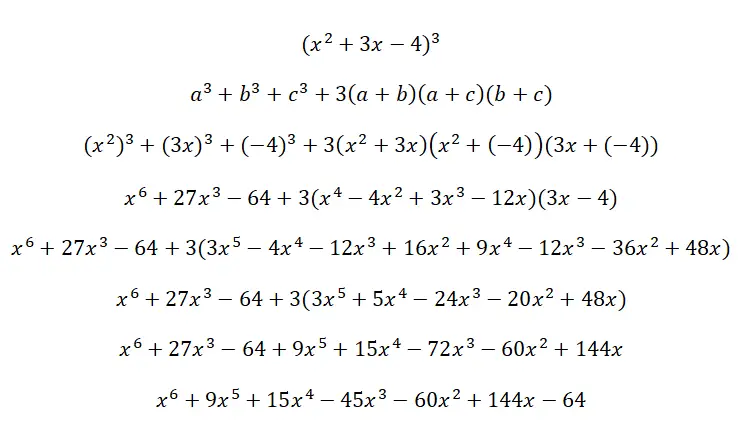
dikkat çekici oranlar

Son olarak, belirli cebirsel kesir türlerini hızlı bir şekilde çözmek için dikkate değer özdeşlikler olan dikkate değer bölümleri açıklayacağız. Daha doğrusu, aynı özelliği paylaşan dört farklı tür vardır: bunların sonuçları tam polinomlardan oluşur (kalan sıfıra eşit). Dikkat çekici katsayı formüllerinin daha önce açıkladığımız dikkat çekici ürün formülleriyle belli bir ilişkisinin olduğunu da belirtmekte fayda var.

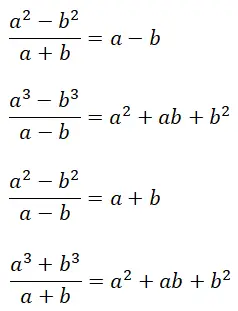
Çözülen Dikkate Değer Oranlara Örnek

Aşağıdaki dikkate değer oranları hesaplayın:

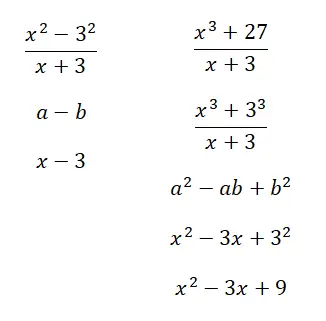
Çözülmüş Dikkat Çekici Ürün Alıştırmaları

Artık farklı ileri gelenlerin nasıl çözüldüğünü bildiğinize göre, biraz pratik yapmanın zamanı geldi. Bu nedenle size açıklanan tüm teoriyi uygulayabilmeniz için 6 alıştırma sunuyoruz. Tüm alıştırmaları çözerken elinizin altında olması için size önemli kimliklerin bir tablosunu gösteriyoruz:

1. Egzersiz

(x – 4) ² , (x + 1) ² ve (x – 3) ² binom karelerini çözün:

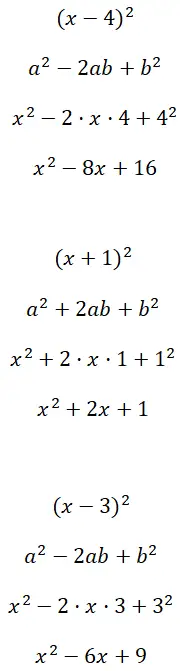
Alıştırma 2

(x – 1) · (x + 1) ve (x + 3) · (x – 3) karelerinin iki farkını hesaplayın:

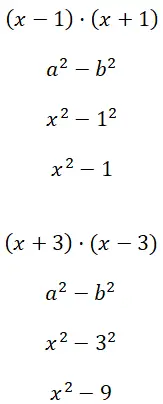
Alıştırma 3

Dikkate değer ürünleri (x – 5) ³ ve (x + 8) ³ küpüne göre geliştirin:

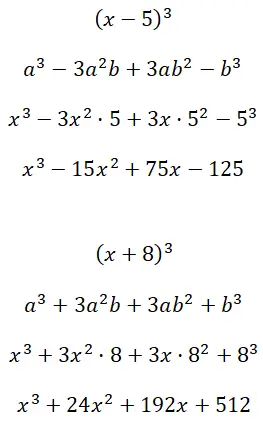
Alıştırma 4

(4x ² + 5y) ² , (5x ³ + y ² ) · (5x ³ – y ² ) ve (5xy ² – 2xy) ² gibi çok faktörlü terimlerden oluşan dikkate değer kimlikler geliştirin:

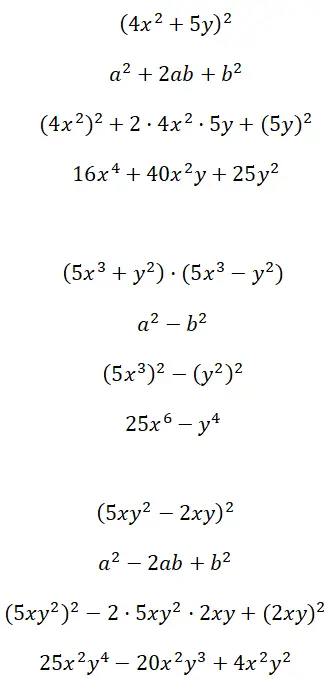
Alıştırma 5

(3x ² + y) ³ ve (5y ³ – 2x ² ) ³ çok faktörlü terimlerin oluşturduğu dikkate değer kübik çarpımları hesaplayın:

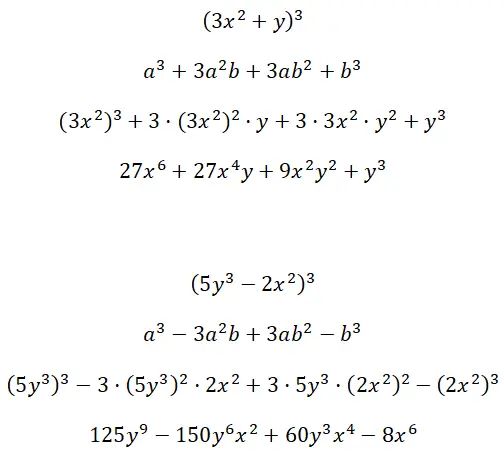
Alıştırma 6

(2x ² + 3x + 5) 2 ve (3x 2 + 5x + 6) trinomiallerinin karelerini ^{çözün :}