Birinci dereceden denklemler veya doğrusal denklemler cebirin temelidir, çünkü bunları anlamazsanız daha karmaşık denklemleri anlamanız çok zor olacaktır. Dolayısıyla, bu tür denklemlerin özelliği, tek terimlilerin gerçek kısmının bir üs sahibi olamamasıdır. Bu nedenle, doğrusal bir denklemde yalnızca değişmez kısmı olmayan tek terimlileri ve üssü olmayan değişmez kısmı olan tek terimlileri bulacağız, örneğin: 3 + x = -5 – 3x .
Ayrıca bu denklemlerin genellikle benzersiz bir çözüme sahip olduğunu, ancak öyle olmadığını da unutmayın. Hangi durumun önümüzde olduğunu bilmek için denklemi çözmeli ve sonunda sonucu analiz etmeliyiz . Yani 2 = 0 gibi imkansız bir eşitlik elde edersek denklemin çözümü yoktur. Öte yandan her zaman doğru olan bir eşitlik elde edersek çözüm tüm reel sayılara eşdeğer olur. Ve son olarak, eğer sonunda X’in eşitliğini ve sayısal bir değeri elde edersek, bu durumda benzersiz bir sonuca sahip olacağız.
Doğrusal bir denklemi çözme prosedürü
Bir denklemi çözmek, (x, y, a, b…) harfiyle temsil edilen bir değişkenin değerini hesaplamaya eşdeğerdir. Dolayısıyla bu değeri bulmak için aşağıdaki adımları izlememiz gerekir:
- Parantezleri ve kesirleri çözün: Başlamak için anlaşılması daha kolay bir denklem elde etmek amacıyla tüm parantezleri ve paydaları kaldırıyoruz. Hangi terimlerin bilinmeyene eşlik ettiğini, hangilerinin etmediğini doğrudan takdir edebildiğimiz için, bu okuma ifadeyi kolayca çözümlemeye devam etmemizi sağlar.
- İfadeyi basitleştirelim: benzer terimleri gruplandırıyoruz (bir yanda bağımsız terimler, diğer yanda x’li terimler). Yani bir tarafta bilinmeyeni olan sayıları bırakacağız ve diğer sayıları karşı tarafa geçireceğiz. Ama unutmayın, taraflarını değiştirmek için işaretlerini değiştirmemiz gerekiyor.
- Her iki tarafta işlem yapın: Tüm işlemleri şu sırayla gerçekleştiriyoruz: kuvvetler/kökler, çarpma/bölme ve toplama/çıkarma. Bunu her iki tarafta da tek bir terim elde edene kadar yaparız ve böylece aynı yapıya sahip bir denklem elde ederiz: 4x = 8.
- Değişkeni izole edin: Son olarak, harfe eşlik eden değeri diğer tarafa bölerek iletin ve böylece son değerini buluruz. Bu adımın sonunda bilinmeyeni çözmüş olacağız ve ne tür bir sonuç kalacağını bileceğiz: benzersiz bir çözüm, geçersiz bir çözüm veya tüm tamsayıları karşılayan bir çözüm.
Birinci Derece Denklem Örnekleri
Aşağıda yapılarının karmaşıklığına göre farklı kategorilere ayrılmış birinci dereceden çözülmüş denklemleri bulacaksınız. Dolayısıyla, doğrusal denklemleri çözmeye yönelik teorik prosedürü ve mevcut farklı türleri bildiğinizden, bunları kolayca çözebilmek için gerekli bilgiye zaten sahip olacaksınız ve pratikle başlayacağız. Bununla birlikte, teorik açıklamaya başlayalım:
Temel Birinci Derece Denklemler
Bu birinci tip doğrusal denklemler yalnızca temel aritmetik işlemlerden (toplama, çıkarma, çarpma ve bölme) oluşur. İşte üzerinde çalışılan iki örnek: Birincisi biraz daha basit, ikincisi ise hesaplama açısından biraz daha karmaşık:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
Parantezli birinci dereceden denklemler
İkincisi, parantez içinde doğrusal denklemlerimiz var. Bunları çözmek öncekilere göre biraz daha karmaşıktır, ancak bunların tek zorluğu hesaplamada yatmaktadır çünkü parantezlerin özelliklerine saygı gösterilmesi gerekmektedir. Daha açık hale getirmek için size üzerinde çalışılan iki örnek gösteriyoruz:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
Üsleri ve kökleri olan birinci derece denklemler
Üçüncü seviye oldukça basittir çünkü yalnızca güçler ve kökler ekler. Bu denklemlerde karşılaşabileceğiniz tek zorluk, üssün veya kökün bir tamsayı parantezini etkilemesidir (size göstereceğimiz ikinci örnek gibi), ancak geri kalan her şey hemen hemen aynı kalır. Aşağıda iki örnek var.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Kesirli birinci derece denklemler
Bulabileceğimiz son doğrusal denklem kategorisi, daha önce yorumladığımız tüm unsurlardan ve ayrıca kesirlerden oluşan bu kategoridir. Bu seviye en karmaşık olanıdır ve bunları çözmenin birkaç yöntemi vardır. İlki ve en basiti, paydaları eşitliğin karşı tarafıyla çarpmaktır, ancak bunu yalnızca iki kesirimiz olduğunda kullanabiliriz. Öte yandan denklemde ikiden fazla kesir varsa ortak bir payda bulmalı ve bu değeri aynı kesrin paydasına bölerek tüm kesirleri çarpmamız gerekir. Aşağıda her türün bir örneği verilmiştir:
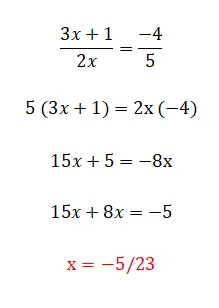
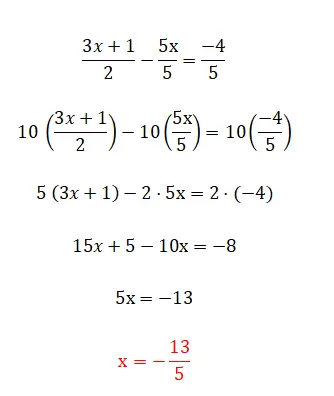
Birinci dereceden denklemlerle ilgili alıştırmalar
Şimdi bazı doğrusal denklem alıştırmaları sunuyoruz. İlk denklemler sonunculara göre daha kolay olacak şekilde artan zorluğa göre düzenlenirler. Bu nedenle en baştan başlamanızı ve ne kadar ileri gidebileceğinizi görmenizi öneririz. Bu nedenle, aşağıdaki denklemleri çözmeyi deneyin ve ardından sonucunuzu sunduğumuz çözümlerle karşılaştırın.
İlk egzersiz
İlk alıştırma çok basit bir doğrusal denklemdir, çünkü yalnızca toplama ve çıkarmalardan oluşur ve eşitliğin iki tarafı arasında yalnızca dört terim vardır:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Benzer terimleri bir arada gruplandırıyoruz.
- Her iki tarafı da basitleştiriyoruz.
- Bilinmeyeni sileriz ve değerini hesaplarız.
ikinci egzersiz
Bu durumda kendimizi parantezlerden oluşan bir denklemle karşı karşıya buluyoruz ve en büyük önceliğimiz onları ortadan kaldırmak, böylece benzer terimleri bir arada gruplayabiliriz:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- Parantezleri çözüyoruz.
- X’leri sola, bağımsız terimleri sağa taşıyoruz.
- Bilinmeyeni açıklığa kavuşturuyoruz.
Sonucu basitleştiriyoruz.
üçüncü egzersiz
Daha sonra, parantezli başka bir ikinci dereceden denklemi çözmeniz gerekecek, ancak bu biraz daha zor. Bunun nedeni iç içe geçmiş parantezlere (diğer parantezlerin içindeki parantezler) sahip olmasıdır. Bu nedenle çözüm sırasını doğru takip etmelisiniz: önce içeridekiler, sonra dışarıdakiler.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- İç parantezleri çözerek başlıyoruz.
- Daha sonra dış parantezleri çözüyoruz.
- Eşitliğin her iki tarafını da sadeleştiriyoruz ve benzer terimleri topluyoruz.
- X’i izole edip değerini hesaplıyoruz.
dördüncü egzersiz
Bu alıştırmada, doğrusal denklemlerin muhtemelen en karmaşık öğesi olan kesirleri görmeye başlıyoruz. Endişelenmeyin çünkü eğer teoriyi okuduysanız, bunun nasıl yapılacağını çok iyi bileceksiniz:
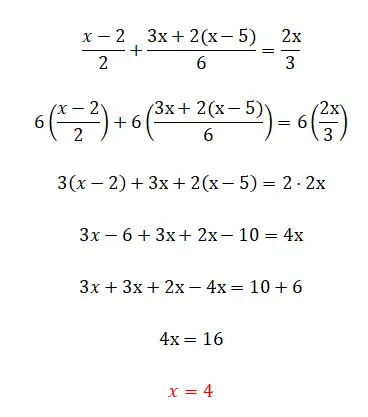
Beşinci egzersiz
Bu beşinci alıştırmada, parantez içindeki kesirleri görüyoruz, bu da çözüm hiyerarşisinin biraz karmaşıklaştığı anlamına geliyor. Bu örneğin iki yöntemle çözülebileceğini belirtmekte fayda var: En küçük ortak katlar yöntemini kullanarak veya doğrudan kesirlerle işlem yaparak. Aşağıda iki prosedürün tamamını görebilirsiniz:
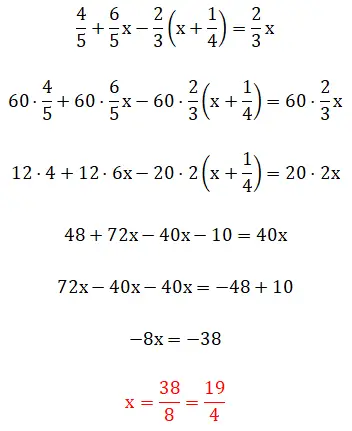
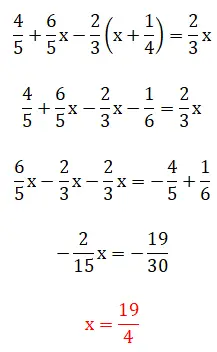
altıncı egzersiz
Daha sonra, iç içe parantezleri kullandığımız için kesirler ve parantez konusuna biraz daha devam ediyoruz. Bu alıştırma bir öncekine göre çok daha fazla komplikasyon getirmiyor, sadece hesaplamalar açısından biraz daha zor ve hepsi bu.
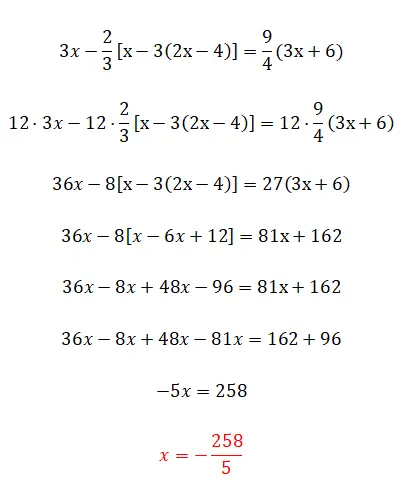
- Tüm terimleri paydaların lcmp’si ile çarpıyoruz.
- Parantezleri kaldırarak ifadeyi basitleştiririz: önce içeridekiler, sonra dışarıdakiler.
- Benzer terimleri her iki tarafta gruplandırıyoruz.
- Her iki taraftaki operasyonları çözüyoruz.
- Ve bilinmeyenin değerini hesaplıyoruz.
yedinci egzersiz
Aşağıdaki alıştırma çok kolay görünebilir, ancak yine de çözmeye çalışmanızı öneririz, çünkü kesinlikle alışılmadık bir sonuç verecektir. Denedikten sonra alıştırmanın altındaki çözüme ve açıklamaya bakın.
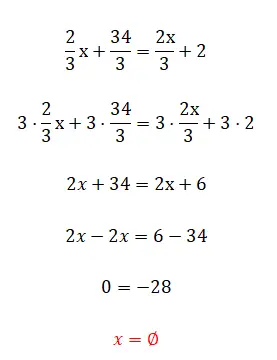
- Tüm kesirleri paydaların lcm’si ile çarpıyoruz.
- Elde edilen ifadeyi basitleştiriyoruz.
- Ve sonunda bilinmeyeni elediğimiz için bunun bize sahte bir eşitlik verdiğini görüyoruz.
Fark etmiş olabileceğiniz gibi, denklemi doğru şekilde tamamlayan bir değer olmadığından bu, yanlış bir eşitlik veya sonuçsuz bir eşitliktir. Bu, girişte bahsettiğimiz durumlardan biridir.
sekizinci egzersiz
Son olarak, oldukça karmaşık olan bu egzersizi sizlere sunuyoruz çünkü bu yazı boyunca gördüğümüz tüm komplikasyonları barındırıyor, ancak aynı zamanda küçük bir hilesi de var. Bu birinci derece denklemi çözebilirseniz teorinin tamamını mükemmel bir şekilde anlamış olduğunuzu yorumlayın. Değilse endişelenmeyin çünkü bu egzersiz oldukça karmaşıktır.
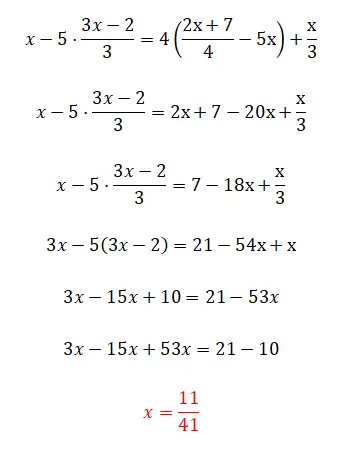
- Denklemin sağ tarafındaki dördünü ortadan kaldırarak başlıyoruz.
- Daha sonra sağ taraftaki x’leri birleştiriyoruz.
- Paydaları ortadan kaldırmak için tüm terimleri üçle çarpıyoruz.
- Parantezleri kaldırıyoruz.
- Benzer terimleri bir araya getiriyoruz.
- Bilinmeyenlerin değerini hesaplıyoruz.
Daha fazla doğrusal denklem alıştırması
Artık yeterince pratik yaptığınıza göre karmaşık doğrusal denklemleri çözebiliyor olmalısınız. Ancak pratik yapmaya devam etmek istiyorsanız bu çalışma sayfasını çözmeye çalışmanızı öneririz. Ancak yeterince kapsadığınızı düşünüyorsanız,operasyonların hiyerarşisini anlamanıza yardımcı olabilecek bir makale de sunabiliriz. Bu sayede her zaman ilk olarak hangi hesaplamayı çözmeniz gerektiğini bilecek ve asla hata yapmayacaksınız .