İrrasyonel fonksiyon veya radikal fonksiyon -

Bu sayfada radikal fonksiyon olarak da adlandırılan irrasyonel fonksiyonun ne olduğu ve bu tür fonksiyonun tüm özellikleri açıklanmaktadır. Ayrıca radikal veya irrasyonel fonksiyonların tanım kümesini nasıl hesaplayacağınızı keşfedecek ve bunlara ek olarak bunları örneklerle bir grafik üzerinde nasıl temsil edeceğinizi görebileceksiniz ve adım adım çözülen alıştırmalar ve problemlerle pratik yapabileceksiniz.

İrrasyonel (veya radikal) fonksiyon nedir?

İrrasyonel bir fonksiyon, radikal bir fonksiyonla aynı anlama gelir ve bu nedenle ortak bir tanımları vardır:

Radikal fonksiyon olarak da adlandırılan irrasyonel fonksiyon , bir kök sembolü altında bağımsız değişken x’e sahip olan bir fonksiyondur.

Zaten bildiğimiz gibi bir kökün sonucu pozitif ya da negatif olabilir. Dolayısıyla irrasyonel (veya radikal) bir fonksiyonun temsilinin iki olası eğrisi vardır:

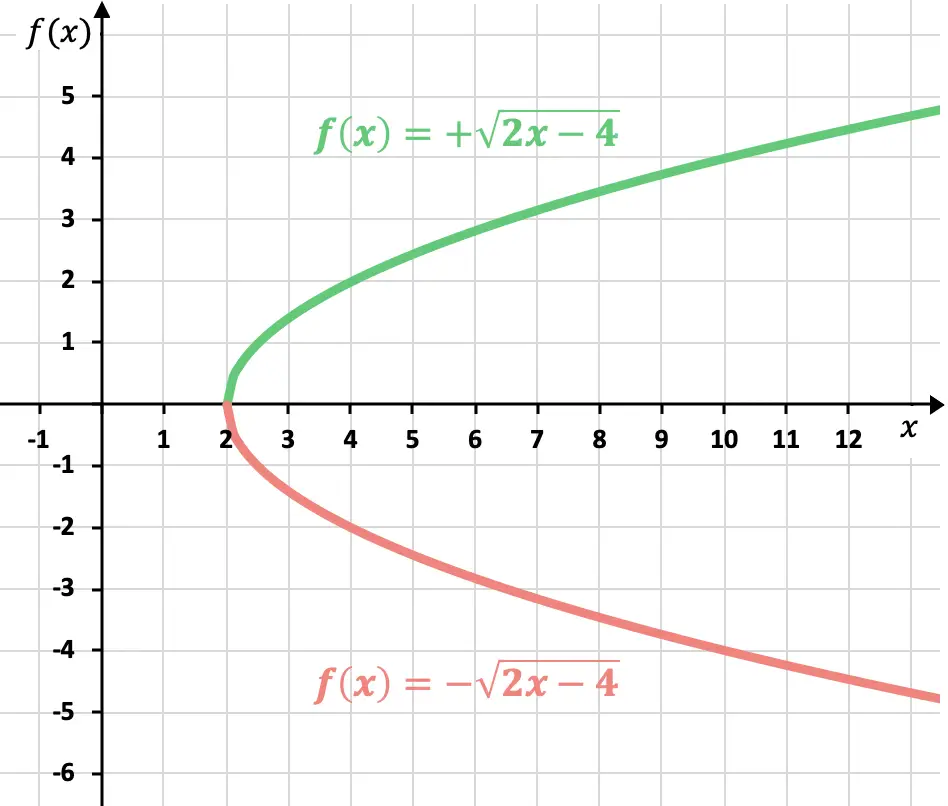
İrrasyonel veya radikal fonksiyon örnekleri

Ancak işaret belirtilmemişse pozitif fonksiyonun temsil edilmesi gerekir.

Öte yandan irrasyonel bir fonksiyon rasyonel bir fonksiyonla karıştırılmamalıdır. İsimleri çok benzer olmasına rağmen tamamen farklı iki fonksiyon türüdür.

İrrasyonel veya radikal bir fonksiyonun alanı

Kökleri olan bir fonksiyonun etki alanı, kök indeksinin paritesine, yani radikal indeksin çift veya tek olmasına bağlıdır.

Çift indeksin köküne sahip bir fonksiyonun etki alanı

Bildiğiniz gibi negatif bir sayının kökü (çift indeksi) yoktur. Bu nedenle, çift indeksli bir radikal fonksiyon, içeriği 0’a eşit veya 0’dan büyük olduğu sürece var olacaktır.

Örnek olarak aşağıdaki radikal veya irrasyonel fonksiyonun tanım kümesinin nasıl hesaplandığını görelim:

$f(x)=\sqrt{x-4}$

Bu bir radikal çift indeks fonksiyonudur, dolayısıyla içeriğinin pozitif veya sıfır olmasına bakmalıyız :

$x-4\ge 0$

Eşitsizliği çözüyoruz:

$x\ge 4$

Dolayısıyla, x 4’ten büyük veya ona eşit olduğunda fonksiyon mevcut olacaktır ve aşağıdaki aralıkla gösterilir:

$\text{Dom } f= [4,+\infty)$

Tek indeks köküne sahip bir fonksiyonun etki alanı

Negatif bir sayının tek indeks kökü mevcut olduğundan, tek indeksli irrasyonel işlevlerde bu sorun yoktur:

$\sqrt[3]{-8}=-2$

Bu nedenle, herhangi bir x değeri için tek indeksin radikal fonksiyonları mevcuttur. Veya başka bir deyişle etki alanı yalnızca gerçek sayılardan oluşur .

Örneğin, indeksi tek olan aşağıdaki radikal fonksiyonun tanım tanım kümesini hesaplayacağız:

$f(x)=\sqrt[3]{3x-4}$

Tek indeksli irrasyonel bir fonksiyon olduğundan, alanı gerçek sayılardan oluşur:

$\text{Dom } f= \mathbb{R}$

İrrasyonel veya radikal bir fonksiyon nasıl temsil edilir?

Bir örnek kullanarak kökleri olan bir fonksiyonun grafik üzerinde nasıl temsil edileceğini görelim.

Aşağıdaki radikal veya irrasyonel fonksiyonu bir grafik üzerinde çizin:

$f(x)=\sqrt{x+2}$

Yapılacak ilk şey fonksiyonun tanım kümesini bulmaktır. Karekök olduğundan, negatif bir sayının karekökü olmadığından, içerdiği her şey pozitif olmalıdır. Bu nedenle radikal fonksiyon, içeriği 0’a eşit veya 0’dan büyük olduğu sürece var olacaktır:

$x+2\ge 0$

$x\ge -2$

Dolayısıyla fonksiyonun tanım kümesi -2’den büyük veya ona eşit olan tüm sayılardan oluşur. Yani:

$\text{Dom } f = [-2,+\infty)$

Fonksiyonun tanım kümesini öğrendikten sonra bir değerler tablosu oluştururuz. Açıkçası, ne kadar çok nokta hesaplarsak fonksiyonun temsili o kadar kesin olacaktır. Ancak etki alanı aralığında 3 veya 4 noktayı hesaplamak yeterlidir:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

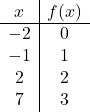
Şimdi elde edilen noktaları bir grafikte temsil ediyoruz :

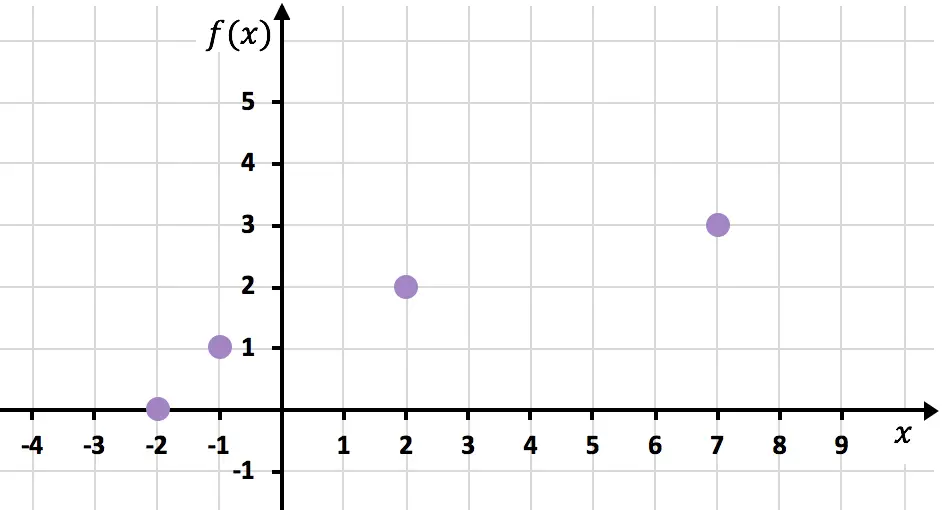
radikal veya irrasyonel bir fonksiyonun nasıl temsil edileceği

Ve son olarak, fonksiyonun büyümeye devam ettiğini belirtmek için noktaları birleştirip eğriyi genişletiyoruz:

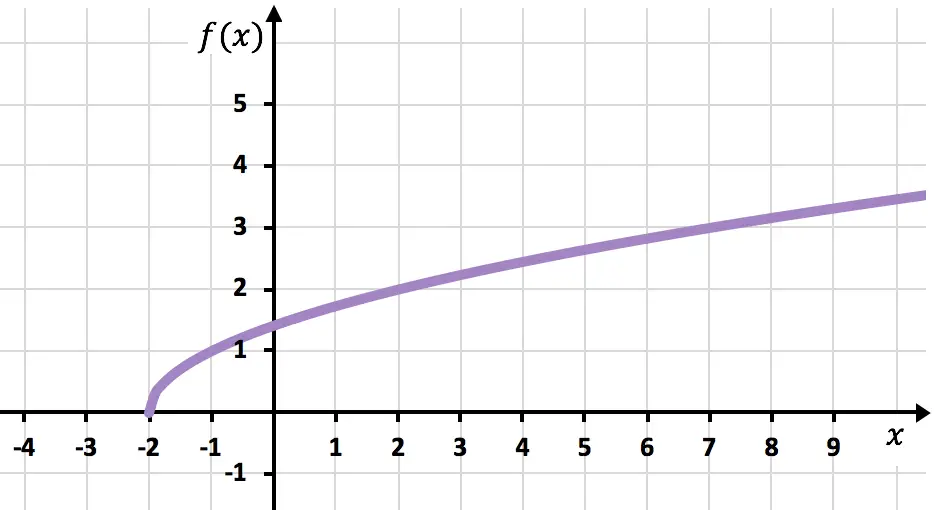
radikal veya irrasyonel bir fonksiyonun grafik temsiline örnek

İrrasyonel veya radikal fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki radikal fonksiyonun tanım kümesini bulun:

$\sqrt{3x+6}$

Çözümü görün

Negatif bir sayının karekökü mevcut değildir. Bu nedenle, kök argümanı pozitif veya sıfır olduğunda fonksiyon mevcut olacaktır:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Alıştırma 2

Aşağıdaki irrasyonel fonksiyonun tanım kümesini bulun:

$\sqrt{-x+2}$

Çözümü görün

Negatif bir sayının karekökünün gerçek bir çözümü yoktur. Bu nedenle, kökün içeriği pozitif veya sıfır olduğu sürece fonksiyon mevcut olacaktır:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

Bir eşitsizlikte negatif bir sayının çarpan veya bölen taraflarını değiştirirsek, eşitsizliğin işaretini de döndürmemiz gerektiğini unutmayın.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Alıştırma 3

Aşağıdaki irrasyonel fonksiyonu bir grafik üzerinde çizin:

$f(x)= \sqrt{x-1}$

Çözümü görün

Öncelikle fonksiyonun tanım kümesini hesaplamamız gerekiyor:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Şimdi fonksiyonun değerlerini domain aralığında vererek bir değerler dizisi oluşturuyoruz:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Son olarak noktaları işaretliyoruz ve fonksiyonu grafik üzerinde çiziyoruz:

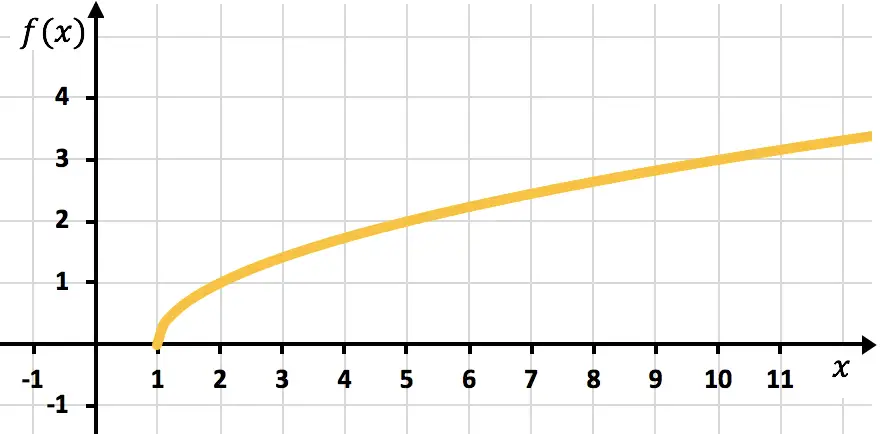
İrrasyonel veya radikal bir fonksiyonun adım adım çözüldüğü egzersiz

Alıştırma 4

Aşağıdaki irrasyonel veya radikal fonksiyonun grafiğini çizin:

$f(x)= -2\sqrt{x}+3$

Çözümü görün

Öncelikle fonksiyonun tanım kümesini hesaplamamız gerekiyor:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Şimdi fonksiyonun değerlerini domain aralığında vererek bir değerler dizisi oluşturuyoruz:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Son olarak noktaları işaretliyoruz ve fonksiyonu grafik üzerinde çiziyoruz:

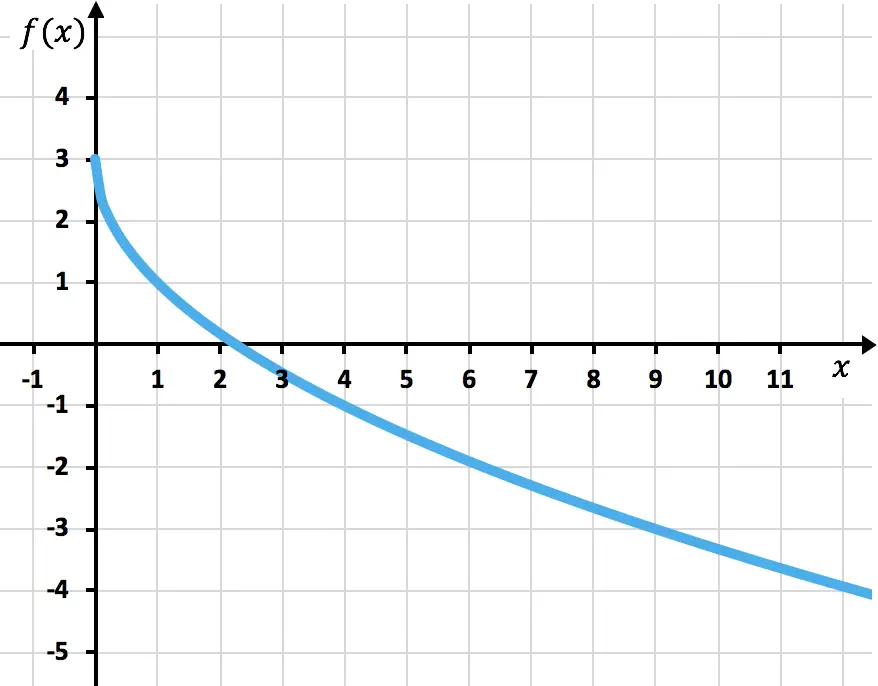
Alıştırma 5

Aşağıdaki irrasyonel veya radikal fonksiyonun grafiğini çizin:

$f(x)= \sqrt{-x+5}$

Çözümü görün

Fonksiyonu çizmeden önce fonksiyonun tanım kümesini hesaplamamız gerekir:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

Bir eşitsizlikte negatif bir sayının çarpan veya bölen taraflarını değiştirirsek, eşitsizliğin işaretini de değiştirmemiz gerektiğini unutmayın.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Şimdi fonksiyonu, fonksiyonun tanım kümesine ait noktalarda değerlendirerek bir değerler tablosu oluşturuyoruz:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

Ve son olarak noktaları temsil edin ve fonksiyonu grafik üzerinde boyayın:

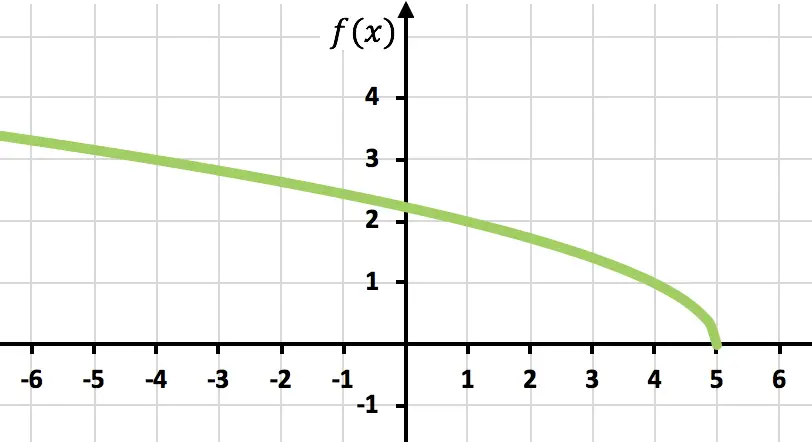
radikal veya irrasyonel fonksiyonların kararlı egzersizleri

Alıştırma 6

Aşağıdaki irrasyonel veya radikal fonksiyonu bir grafik üzerinde çizin:

$f(x)= \sqrt{x^2-5x+4}$

Çözümü görün

İlk önce fonksiyonun tanım kümesini hesaplamamız gerekir:

$x^2-5x+4\ge 0$

Bu durumda ikinci dereceden bir eşitsizlik elde ettik, dolayısıyla bunu çözmek için ikinci dereceden denklem formülünü uygulamamız gerekiyor:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

Elde edilen köklerle çizgiyi üç parçaya bölüyoruz:

Hangi bölümlerin eşitsizliği karşıladığını ve dolayısıyla alana ait olduğunu görmek için eşitsizliğin her bölümü için bir sayı koyarız:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”> ❌ <p class=$ $x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

✅

Dolayısıyla eşitsizliğe saygı duyan kesimler taraflara ait:

Bu nedenle fonksiyonun tanım kümesi şu şekildedir:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

Fonksiyonun tanım kümesini hesapladıktan sonra, işlevin tanım kümesi aralığındaki değerlerini veren bir değerler tablosu oluştururuz:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Son olarak elde edilen noktaları grafikte temsil ediyoruz ve fonksiyonu çiziyoruz:

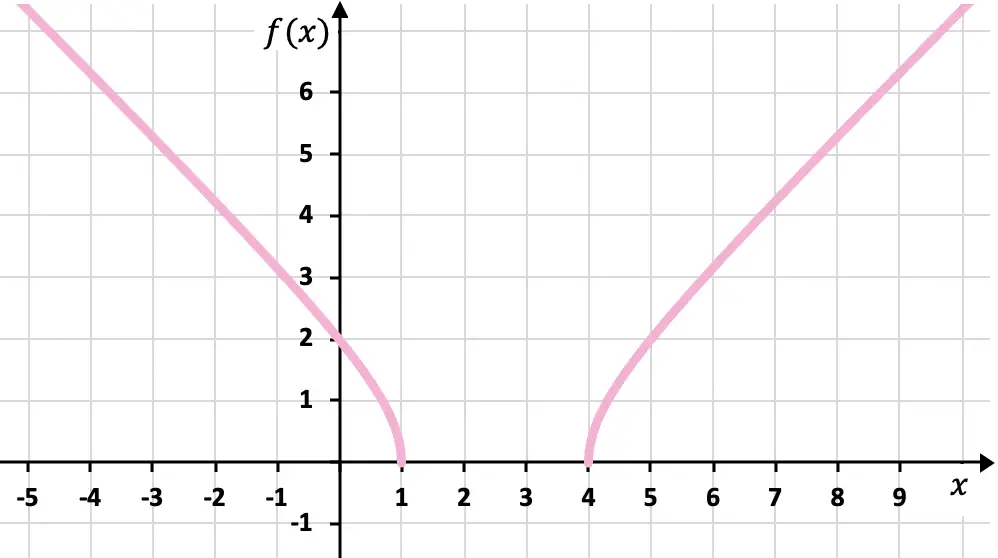
çift indeksli irrasyonel veya radikal bir fonksiyonun grafiği

Egzersiz 7

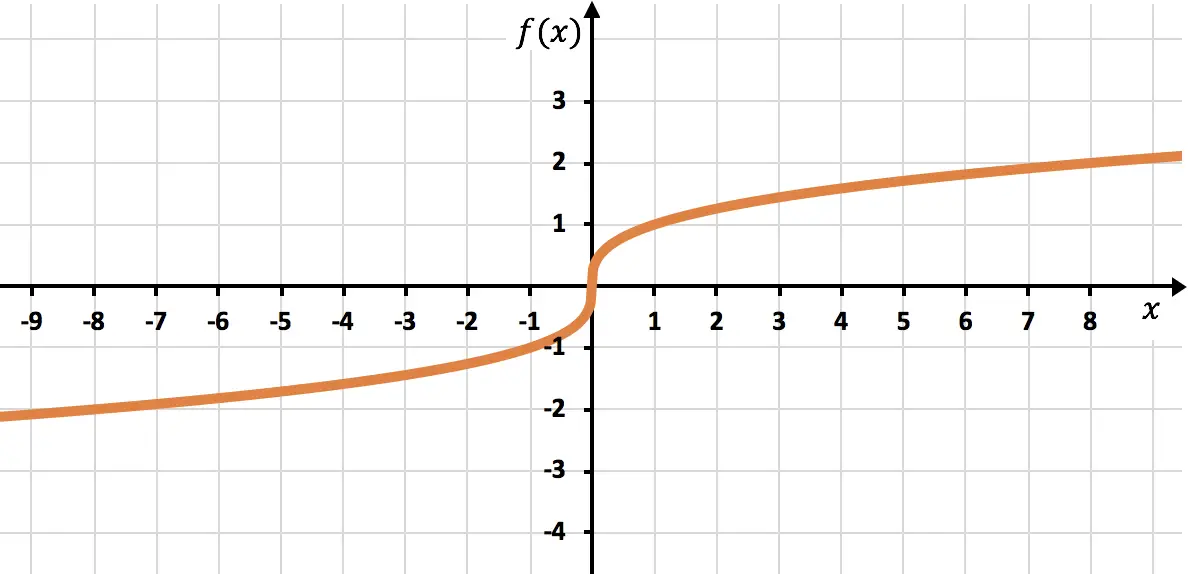
Bir kökün oluşturduğu aşağıdaki fonksiyonu grafik üzerinde temsil edin:

$f(x)= \sqrt[3]{x}$

Çözümü görün

Bu, kökü tek indeksli olan irrasyonel bir fonksiyondur, dolayısıyla fonksiyonun tanım kümesi gerçek sayılardan oluşur:

$\text{Dom } f = \mathbb{R}$

Bu nedenle değerler tablosunu oluşturmak için herhangi bir noktayı alabiliriz. Bu durumda küp kök olduğundan birçok nokta arayacağız:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Son olarak bulunan noktaları işaretliyoruz ve fonksiyonu grafik üzerinde çiziyoruz:

tek indeksli irrasyonel veya radikal bir fonksiyonun grafiğini çizme

Egzersiz 8

İrrasyonel (veya radikal) fonksiyonlarla ilgili aşağıdaki problemi çözün:

Bir cep telefonu pilinin tüketimi aşağıdaki fonksiyonla verilir:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Tüketimin miliamper (mA) cinsinden ifade edildiği ve

$t$

dakika cinsinden geçen süredir.

Sabitin değerini belirleyin

$K$

böylece 4 dakika sonra tüketim 35 mA olur.

Çözümü görün

4 dakika sonra tüketimin 35 mA olması, t 4 olduğunda f(t)’nin 35 olduğu anlamına gelir. Yani f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Şimdi elde ettiğimiz denklemi çözmemiz gerekiyor. Eğer yakından bakarsanız, bunun bir kökü olduğu için irrasyonel bir denklem olduğunu görürsünüz. Bu tür denklemlerde yapılacak ilk şey, bu durumda zaten izole edilmiş olan bir tarafın kökünü izole etmektir. İzole edildikten sonra denklemin her iki tarafının karesini almalıyız:

$\left( \sqrt{4-K} \right)^2= 35^2$