Üç kuralı, belirli değerler arasında var olan orantı ilişkilerini bilmemizi sağlar. Bu sayede günlük hayatın her alanında neredeyse her gün uyguluyoruz. Örnek vermek gerekirse; yüzde hesaplamaları yapın , birimler arası (kütle, hacim, zaman vb.) dönüşümler yapın ve genel olarak eşdeğerliklere dayalı hesaplamalar yapın. Bu son uygulama, bu matematik kaynağını hemen hemen her konuda kullanmamıza olanak sağlayan uygulamadır.
Yani üçün kurallarını nasıl çözeceğinizi öğrenmek istiyorsanız yazının sonuna kadar kalmanızı öneririz. Bunların nasıl çözüleceğini, ne türlerinin olduğunu, uygulamalarını açıklayacağımız ve hatta bazı çözülmüş örnekler bile bulacaksınız. Kısacası bu makaleyi okumayı bitirdiğinizde bu matematik kavramı hakkında bilmeniz gereken her şeyi biliyor olacaksınız.
üç hesaplayıcının kuralı
Üç hesap makinesinin bu kurallarını kullanarak (birincisi doğru orantı, ikincisi dolaylı orantı), tüm alıştırmalarınızı kontrol edebilecek ve düzeltebileceksiniz. İşlemi çok basittir, dört kutudan üçüne bildiğiniz verileri girmeniz yeterlidir ve hesapla butonuna tıkladığınızda x’in değeri görüntülenecektir. Ancak bu tür bir hesaplamayı nasıl yapılandıracağınızı hâlâ bilmiyorsanız endişelenmeyin, çünkü bir sonraki bölümde bunu size ayrıntılı olarak açıklayacağız.
Üç hesap makinesinin doğrudan kuralı
Üç Hesaplayıcının Ters Kuralı
Üç kuralı nasıl yapılır?
Üç kuralını çözmek için öncelikle hangisini kullanacağınızı belirlemelisiniz: üçün doğrudan kuralı veya üçün dolaylı kuralı. Ayrıca hangi orantı türünü kullanacağımızı da ayırt etmeliyiz: basit üç kuralı veya üçün bileşik kuralı. Herkes bu seçeneklerden birine sahip olduğundan, verileri düzenlemenin farklı bir yolu ve farklı bir formülü vardır. Bu nedenle, her türün ne zaman seçileceğini bilmek için üç kuralının nasıl çözüleceğine ilişkin aşağıdaki açıklamayı okumanızı öneririz.
1. Farklı değişkenler arasındaki ilişkileri tanımlayın
Üç kuralını çözmenin ilk adımı değişkenler arasında bir tür diyagram veya ilişki oluşturmaktır. Genel olarak bu genellikle aşağıdaki resimde görülen tipik diyagramla yapılır. Bu sayede hesaplamanın daha net bir yapısına sahip olacağız ve daha sonra hesaplamaları gerçekleştirebileceğiz. Sadece A, B ve C harflerini karşılık gelen değerlerle değiştirmeniz gerekir: sol sütunda bir bütün olarak bildiğiniz büyüklüğün sayısal değerleri (her iki değer) ve sağ sütunda değerler gidecektir bilinmeyeni olan büyüklükte. Ayrıca çizgilere de saygı duymanız gerekir, bu nedenle A, B değişkeniyle ilgili olan soldaki büyüklük değeri olmalıdır.
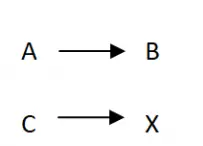
2. Üç kuralının orantılılığını oluşturun
Bir sonraki adım değişkenler arasındaki orantıyı belirlemek olacak, bunu her büyüklükteki değişkenler arasındaki sayısal değerdeki değişimi analiz ederek yapacağız. Eğer düz bir üç kuralıyla karşılaşırsak, miktarlardan biri arttığında diğeri de artacaktır. Ancak ters üç kuralıyla karşılaşırsak, bir nicelik arttığında diğeri azalır. Formül duruma göre değişeceğinden bunu akılda tutmak önemlidir.
3. Basit kurallar veya üçten oluşan kurallar
Son olarak, orantılılık kullanarak ilişkilendirdiğimiz değişken sayısına bağlı olarak üç kuralını iki türe ayıracağız. Basit üç kuralı durumunda, X değişkeninin değerini başka bir miktarın orantılılığından elde ederiz. Üçten oluşan kural, iki veya daha fazla niceliğin orantılılığına dayalı olarak X değişkenini hesaplamamıza izin verir. Daha sonra size bu iki kavramın formüllerini ve grafiksel temsilini göstereceğiz, böylece bu konuda hiçbir şüphe kalmaz:

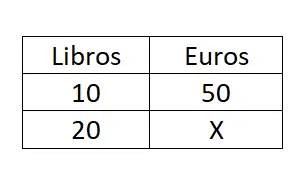
Basit üç kuralı örneği
On kitap elli avroya mal oluyorsa, 20 kitap alırsak ne kadar para harcayacağız?
Sonucu elde etmek için basit ve anlaşılır bir üç kuralını çözmemiz gerekiyor. Bu nedenle X = (B · C) / A formülünü kullanacağız:
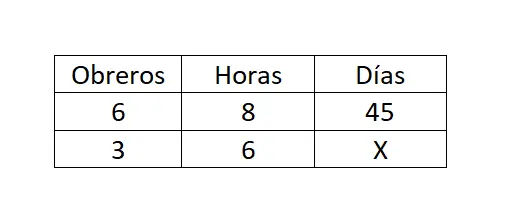
Üçten oluşan bir kural örneği
Günde 8 saat çalışan 6 işçi bir evi 45 günde yaparsa, günde 6 saat çalışan 3 işçi aynı inşaatı kaç günde tamamlar?
Bu durumda, üçün bileşik ve dolaylı kuralına sahibiz. Bu nedenle X = (A 1 · B 1 · C 1 ) / (A 2 · B 2 ) formülünü kullanacağız:
Üç kuralının uygulamaları
Girişte de belirttiğimiz gibi üç kuralı birçok şeyi hesaplamamıza olanak tanır ve dolayısıyla bunları günlük hayatın her alanına uygularız. Bu tür uygulamaların ortak özelliği olmakla birlikte orantı kullanılarak hesaplanmasıdır. Birkaç örnek vermek gerekirse:
- Yüzdelerin hesaplanması
- birimler arasındaki dönüşümler
- İlaç dozlarını hesaplayın
- Komisyonları hesapla
- notları hesapla
Ve aslında eşdeğerlik veya benzeri gerektiren neredeyse tüm işlemler.
Bilimsel hesap makinesinde üç kuralı
En yaygın bilimsel hesap makinelerinde genellikle üçün kurallarını çözmemizi sağlayan bir fonksiyon veya anahtar yoktur. Dolayısıyla, kişiselleştirilmiş işlevler ekleyebileceğiniz gelişmiş bir hesap makineniz yoksa, 3’ün kurallarını çözmeniz pek mümkün olmayacaktır. Bu nedenle, işlemi ayrı ayrı yapmanız gerekecektir (bir kağıt üzerinde veya kafanızda). daha sonra hesap makinesinde hesaplama kısmını yapın. İlk başta biraz yavaş görünebilir, ancak pratik yaptığınızda ve üç kuralını zihninizde çizildiğini hayal edebildiğinizde, onları bir saniyede çözebileceksiniz .
Son olarak şunu söyleyeyim, üç alıştırmanın daha fazla kuralını incelemek isterseniz, pratik yapabileceğiniz alıştırmaların bağlantısını size bırakıyoruz. Bununla birlikte, bu makalenin ve çevrimiçi 3 Kuralı hesaplayıcımızın bu matematik kavramını daha iyi anlamanıza yardımcı olduğunu umuyoruz.