▷ Nedir ve ikinci dereceden bir fonksiyonun (veya parabolün) nasıl temsil edileceği

Bu sayfada ikinci dereceden fonksiyonun ne olduğu ve tüm özellikleri açıklanmaktadır: eğrilik, tepe noktası, eksenlerle kesişme noktaları vb. Ayrıca ikinci dereceden bir fonksiyonun grafik üzerinde nasıl temsil edileceğini de öğreneceksiniz. Son olarak ikinci dereceden fonksiyonlarla ilgili örneklerle, adım adım alıştırmalarla ve problemlerle pratik yapabilirsiniz.

İkinci dereceden fonksiyon nedir?

İkinci dereceden bir fonksiyonun tanımı aşağıdaki gibidir:

Matematikte, ikinci dereceden (veya parabolik) bir fonksiyon, 2. dereceden bir polinom fonksiyonudur, yani en yüksek dereceli terimin ikinci dereceden olduğu bir fonksiyondur. Bu nedenle ikinci dereceden bir fonksiyonun formülü şöyledir:

$f(x)=ax^2+bx+c$

Altın:

$ax^2$

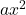
ikinci dereceden terimdir.
$bx$

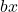
doğrusal terimdir.
$c$

bağımsız terimdir.

İkinci dereceden bir fonksiyonun alanı her zaman gerçek sayılardan oluşur.

$\text{Dom } f=\mathbff{R}$

İkinci dereceden bir fonksiyonun içbükeyliği ve dışbükeyliği

İkinci dereceden veya parabolik bir fonksiyonun eğriliğini analiz etmek çok basittir çünkü yalnızca ikinci dereceden katsayıya bağlıdır.

Eğer katsayı
$a$

pozitifse, ikinci dereceden fonksiyon dışbükeydir (formda

$\bm{\cup}$

). Zirve bu nedenle minimum düzeydedir.
Eğer katsayı
$a$

negatifse, ikinci dereceden fonksiyon içbükeydir (şeklindedir)

$\bm{\cap}$

). Bu nedenle zirve maksimumdur.

İkinci dereceden fonksiyon veya dışbükey parabol

İkinci dereceden fonksiyon veya içbükey parabol

Not: Matematik camiası hala tam olarak aynı fikirde değil ve bu nedenle bazı profesörler bunun tersini söylüyor: bir fonksiyona içbükey bir fonksiyon diyorlar.

$\bm{\cup}$

ve formuna sahip bir dışbükey fonksiyon

$\bm{\cap}$

. Her durumda önemli olan, adı ne olursa olsun, hangi formun işlevi olduğudur.

İkinci dereceden bir fonksiyonun tepe noktası

İkinci dereceden bir fonksiyonun grafiğini çizmek için parabolün tepe noktasının koordinatlarını bilmek gerekir.

İkinci dereceden bir fonksiyonun tepe noktasını bulmak için aşağıdaki formülü kullanarak noktanın X koordinatını hesaplamamız gerekir:

$\displaystyle x=\frac{-b}{2a}$

Daha sonra fonksiyonun o noktadaki görüntüsünü hesaplayarak diğer köşe koordinatını bulabiliriz:

$\displaystyle f\left(\frac{-b}{2a}\right)$

Dolayısıyla ikinci dereceden bir fonksiyonun (veya parabolün) tepe noktasının koordinatları şöyledir:

$\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)$

İkinci dereceden bir fonksiyonun eksenleriyle kesme noktaları

Bir parabol her zaman y ekseniyle (Y ekseni) kesişir ve bu şu durumlarda gerçekleşir:

$x=0.$

Bu nedenle, Y eksenine sahip ikinci dereceden bir fonksiyonun kesme noktasını hesaplamak için,

$f(0).$

Örneğin aşağıdaki ikinci dereceden fonksiyonun OY ekseni ile kesişme noktası şöyledir:

$f(x)=x^2-2x+1$

$f(0)=0^2-2\cdot 0+1 = 1$

$\bm{(0,1)}$

Öte yandan, x eksenine (X ekseni) sahip ikinci dereceden bir fonksiyonun kesme noktası şu durumda ortaya çıkar:

$f(x)=0.$

Yani X ekseni ile kesişme noktasını hesaplamak için denklemi çözmeniz gerekir.

$f(x)=0.$

Örnek olarak aşağıda aynı ikinci dereceden fonksiyonun OX ekseni ile kesme noktasının hesaplanması verilmiştir:

$f(x)=x^2-2x+1$

$0=x^2-2x+1$

İkinci dereceden denklemi genel formülle çözüyoruz:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1$

Dolayısıyla ikinci dereceden fonksiyonun X ekseni ile kesişme noktası şu şekildedir:

$\bm{(1,0)}$

Bu durumda ikinci dereceden denklemin yalnızca bir çözümünü elde ettik ama iki çözümü de bulabilirdik. Bu durumda bu, ikinci dereceden fonksiyonun X eksenini iki farklı noktada kestiği anlamına gelir.

İkinci dereceden veya parabolik bir fonksiyonun temsiline örnek

Bir örnek kullanarak ikinci dereceden bir fonksiyonun grafik üzerinde nasıl temsil edileceğini görelim.

Aşağıdaki fonksiyonun grafiğini çizin:

$f(x)=x^2-4x+5$

Yapılacak ilk şey parabolün tepe noktasını hesaplamaktır. Bunu yapmak için yukarıda gördüğümüz formülü kullanıyoruz:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2$

Köşenin nerede olacağını öğrendikten sonra bir değerler tablosu oluşturmamız gerekir: Fonksiyonun değerini köşe noktasında ve onu çevreleyen noktalarda hesaplıyoruz:

$f(x)=x^2-4x+5$

$x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2$

$x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2$

$x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5$

$x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}$

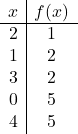
Parabolü daha iyi çizmek için ikinci dereceden fonksiyonun kesme noktalarını Kartezyen eksenlerle de hesaplayabilirsiniz, ancak bu kesinlikle gerekli değildir.

Şimdi elde edilen noktaları bir grafikte temsil ediyoruz :

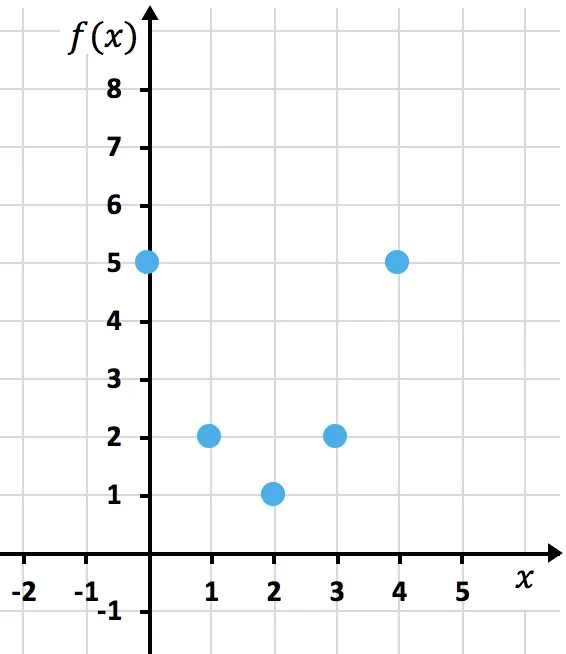
İkinci dereceden veya parabolik bir fonksiyonun nasıl temsil edileceğine dair örnek

Son olarak parabolü oluşturan noktaları birleştiriyoruz. Daha sonra parabolün yukarıya doğru devam ettiğini belirtmek için dallarını uzatıyoruz:

ikinci dereceden veya parabolik bir fonksiyonun temsili

İkinci dereceden fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki ikinci dereceden fonksiyonun tepe noktasını bulun:

$f(x)=2x^2+8x+4$

Çözümü görün

İlk önce aşağıdaki formülü kullanarak tepe noktasının X koordinatını hesaplarız:

$x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2$

Şimdi de noktadaki fonksiyonu değerlendirerek diğer koordinatı hesaplıyoruz:

$\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}$

İkinci dereceden fonksiyonun tepe noktası bu nedenle:

$\bm{(-2,-4)}$

Alıştırma 2

Aşağıdaki fonksiyonun kesme noktalarını eksenlerle bulun:

$f(x)=x^2-4x+3$

Çözümü görün

Y ekseni ile kesme noktasını hesaplamak için şunu hesaplamamız gerekir:

$f(0):$

$f(0)=0^2-4\cdot 0+3 = 3$

Dolayısıyla fonksiyon şu noktada Y ekseninden geçer:

$\bm{(0,3)}$

Ve X eksenindeki kesme noktalarını bulmak için çözmemiz gerekenler

$f(x)=0:$

$f(x)=x^2-4x+3$

$0=x^2-4x+3$

İkinci dereceden denklemin köklerini aşağıdaki formülle hesaplıyoruz:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}$

Dolayısıyla fonksiyon X eksenini iki noktada keser:

$\bm{(1,0) \qquad (3,0)}$

Alıştırma 3

Aşağıdaki ikinci dereceden fonksiyonun grafiğini çizin:

$f(x)=-x^2+4x+1$

Çözümü görün

Bu ikinci dereceden bir fonksiyondur. sonuç olarak, onu temsil etmek için öncelikle parabolün tepe noktasının apsisini aşağıdaki formülle hesaplamanız gerekir:

$x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2$

Şimdi değerler tablosunu oluşturuyoruz. Bunu yapmak için değerini hesaplıyoruz.

$f(x)$

üstte ve üst çevresinde:

$x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5$

$x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4$

$x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4$

$x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1$

$x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}$

Son olarak grafikteki noktaları işaretleyip parabolü çiziyoruz:

Alıştırma 4

Aşağıdaki ikinci dereceden fonksiyonun grafiğini çizin:

$f(x)=-2x^2-8x-1$

Çözümü görün

Bu ikinci dereceden bir fonksiyondur. sonuç olarak, onu temsil etmek için önce parabolün tepe noktasının apsisini aşağıdaki formülle bulmalısınız:

$x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2$

Şimdi değerler tablosunu oluşturuyoruz. Bunu yapmak için değerini hesaplıyoruz.

$f(x)$

üstte ve üst çevresinde:

$x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7$

$x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5$

$x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5$

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1$

$x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}$

Son olarak grafikteki noktaları işaretleyip parabolü çiziyoruz:

ikinci dereceden fonksiyonun adım adım çözüldüğü egzersiz

Alıştırma 5

Aşağıdaki tamamlanmamış ikinci dereceden fonksiyonu bir grafik üzerinde çizin:

$f(x)=x^2+2$

Çözümü görün

İkinci dereceden bir polinom fonksiyonudur. sonuç olarak, onu temsil etmek için öncelikle parabolün tepe noktasının apsisini aşağıdaki formülle hesaplamanız gerekir:

$x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0$

Bu durumda fonksiyon birinci dereceden bir terime sahip olmadığından eksiktir. Bunun için

$b=0 .$

Şimdi değerler tablosunu oluşturuyoruz. Bunu yapmak için değerini hesaplıyoruz.

$f(x)$

üstte ve üst çevresinde:

$x= 0 \ \longrightarrow \ f(0)=0^2+2=2$

$x= 1 \ \longrightarrow \ f(1)=1^2+2=3$

$x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3$

$x= 2 \ \longrightarrow \ f(2)=2^2+2=6$

$x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}$

Son olarak grafikteki noktaları işaretleyip parabolü çiziyoruz:

Tamamlanmamış ikinci dereceden bir fonksiyonu temsil etmek için çözülmüş alıştırmalar

Alıştırma 6

İkinci dereceden fonksiyonlarla ilgili aşağıdaki problemi çözün:

Bir ürünü üretmenin maliyeti aşağıdaki fonksiyonla tanımlanır:

$f(x)=x^2-12x+76$

Altın

$x$

üretilen birimler (bin olarak) ve

$f(x)$

birimlerin üretim maliyetidir (bin Euro).

Üretim maliyeti fonksiyonunu bir grafik üzerinde temsil eder.
Maliyetleri en aza indirmek için kaç bin adet üretilmesi gerektiğini belirleyin.

Çözümü görün

Bu ikinci dereceden bir fonksiyondur. sonuç olarak, onu temsil etmek için önce parabolün tepe noktasının apsisini aşağıdaki formülle bulmalısınız:

$x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6$

Şimdi değerler tablosunu oluşturuyoruz. Bunu yapmak için değerini hesaplıyoruz.

$f(x)$

üstte ve üst çevresinde:

$x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40$

$x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41$

$x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41$

$x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44$

$x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44$

$\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}$

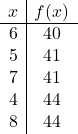
Şimdi grafikteki noktaları işaretleyip parabolü çiziyoruz:

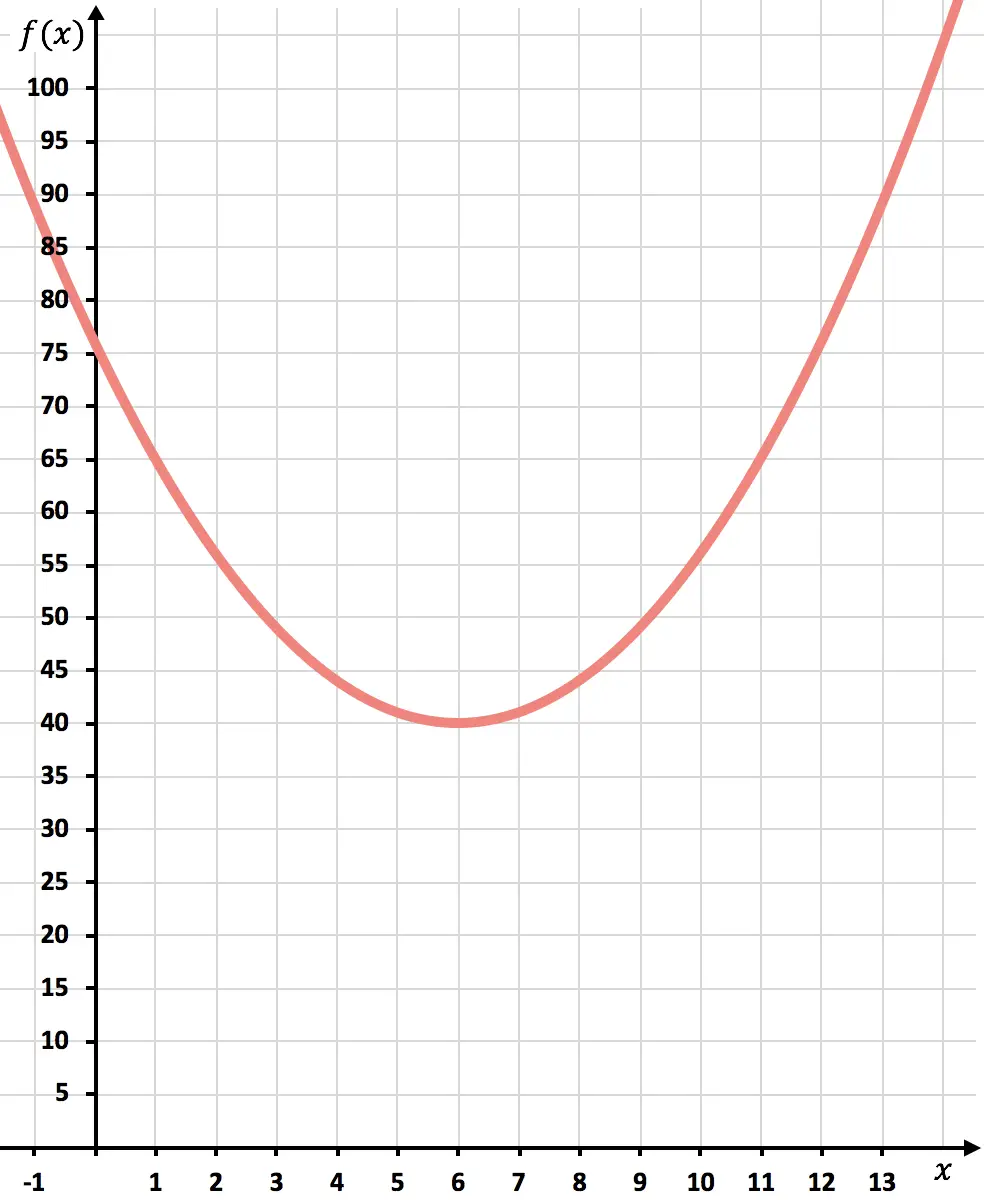
İkinci dereceden veya parabolik fonksiyon problemi

Fonksiyon temsil edildikten sonra maliyetlerin ne kadar minimize edildiğini göreceğiz.

Grafiğin gösterdiği gibi minimum maliyetlere parabolün tepesinde ulaşılacaktır. Çünkü fonksiyonun en küçük değeri aldığı yer burasıdır.

Sonuç olarak 6.000 adet üretilerek maliyetler minimuma indirilecek.

Egzersiz 7

Aşağıdaki ikinci dereceden fonksiyon problemini çözün:

Bir sporcu, yörüngesi aşağıdaki fonksiyonla temsil edilebilecek bir cirit atışı gerçekleştirir:

$h(x) = -0,025x^2+2x+2$

Altın

$x$

ciritin kapsadığı metreler ve

$h$

yüksekliği (aynı zamanda metre cinsinden).

Ciritin ulaşabileceği maksimum yükseklik nedir?

Çözümü görün

Bu ikinci dereceden bir fonksiyon olduğundan ciritin yörüngesi bir parabol olacaktır.

Ayrıca ikinci dereceden terimin katsayısı negatif (-0,025) olduğundan parabol ters U şeklinde olacak ve dalları aşağı doğru inecektir. Böylece cirit en yüksek yüksekliğe ulaşacaktır çünkü burası parabolün en yüksek noktası olacaktır.

Bu nedenle parabolün tepe noktasının apsisini aşağıdaki formülle hesaplıyoruz:

$x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40$

Daha sonra fonksiyonu değerlendirerek ciritin o noktada ne kadar yüksekte olacağını hesaplıyoruz.

$x=40:$

$h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42$

Dolayısıyla ciritin ulaşabileceği maksimum yükseklik 42 metredir.

Egzersiz 8

İkinci dereceden fonksiyonlarla ilgili aşağıdaki problemi çözün:

Bir şirketin üretim maliyetleri (avro cinsinden) aşağıdaki fonksiyonla tanımlanır:

$C(q)=40000+20q+q^2$

Altın

$q$

üretilen birimlerdir.

Her birimin satış fiyatı ise 520€.

Firma 150 adet satarsa ne kadar kar elde eder?
Maksimum kar için kaç adet satılmalıdır?

Çözümü görün

Şirket satılan her birim için 520 € kazanıyor. Dolayısıyla geliri tanımlayan fonksiyon şu şekildedir:

$I(q)=520\cdot q = 520q$

Altın

$q$

satılan birimler nelerdir?

Ama bize kârı, yani gelir eksi maliyetleri soruyorlar. Bu nedenle, şirketin kârını tanımlayan fonksiyonu elde etmek için gelir eksi maliyetleri çıkarıyoruz:

$B(q)=I(q)-C(q)$

$B(q)=520q - (40000+20q+q^2)$

$B(q)=520q - 40000-20q-q^2$

$B(q)=-q^2 + 500q - 40000$

Şirketin kârını tanımlayan fonksiyonu bildiğimizde, şirketin 150 birim satarak elde edeceği kârı hesaplamak için fonksiyon ifadesine 150 yazmanız yeterlidir:

$\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}$

Yani şirket 150 adet satarak 12.500€ kar elde edecek.

Açıklamada ayrıca maksimum kârın kaç birim elde edildiğini hesaplamamız da isteniyor.

Kârı tanımlayan fonksiyon ikinci dereceden bir fonksiyon olduğundan parabol şeklinde olacaktır. İkinci dereceden terimin katsayısı negatif (-1) olduğundan parabol ters U şeklinde olacak ve dalları aşağıya doğru gidecektir. Dolayısıyla parabolün en yüksek noktası burası olduğundan maksimum kazanç tepede yapılacaktır.

Bu nedenle parabolün tepe noktasının apsisini aşağıdaki formülle hesaplıyoruz:

$x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250$

Yani şirket 250 adet satarak maksimum karı elde edecek.

Öte yandan basın bülteni öyle bir şey istemese bile bu 250 adetin satılmasıyla elde edilecek karı şu şekilde belirleyebiliriz:

$B(250) =-(250)^2 + 500\cdot250- 40000= 22500$

€

İkinci dereceden fonksiyon veya parabol

İkinci dereceden fonksiyon nedir?

İkinci dereceden bir fonksiyonun içbükeyliği ve dışbükeyliği

İkinci dereceden bir fonksiyonun tepe noktası

İkinci dereceden bir fonksiyonun eksenleriyle kesme noktaları

İkinci dereceden veya parabolik bir fonksiyonun temsiline örnek

İkinci dereceden fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Egzersiz 7

Egzersiz 8

Yorum bırakın Yanıtı iptal et