Matris güçleri -

Bu sayfada matrislerin kuvvetlerinin nasıl yapıldığını göreceğiz. Ayrıca matrislerin kuvvetlerine ilişkin örnekleri ve adım adım çözülmüş alıştırmaları da bulacaksınız; bunlar, bunu mükemmel bir şekilde anlamanıza yardımcı olacaktır. Ayrıca bir matrisin n’inci kuvvetinin ne olduğunu ve onu nasıl bulacağınızı da öğreneceksiniz.

Bir matrisin gücü nasıl hesaplanır?

Bir matrisin kuvvetini hesaplamak için matrisi üssün söylediği sayı kadar kendisiyle çarpmanız gerekir. Örneğin:

$A^4 = A \cdot A \cdot A \cdot A$

Bu nedenle bir matrisin gücünü elde etmek için matris çarpımının nasıl çözüleceğini bilmeniz gerekir. Aksi halde güç matrisini hesaplayamazsınız.

Bir matrisin gücünün hesaplanmasına örnek:

Bu nedenle kare bir matrisin gücü, matrisin kendisiyle çarpılmasıyla hesaplanır. Benzer şekilde küp matris, matrisin kendisinin kare matrisine eşittir. Benzer şekilde, dörde yükseltilmiş bir matrisin kuvvetini bulmak için, üçe yükseltilmiş matrisin matrisin kendisi ile çarpılması gerekir. Ve benzeri.

Matris kuvvetinin bilmeniz gereken önemli bir özelliği vardır: Bir matrisin kuvveti ancak kare olduğunda, yani satır sayısı ve sütun sayısı aynı olduğunda hesaplanabilir .

Bir matrisin kuvveti n nedir?

Bir matrisin n’inci kuvveti, bir matrisin herhangi bir kuvvetini kolayca hesaplamamızı sağlayan bir ifadedir.

Genellikle matrislerin kuvvetleri bir modeli takip eder. Dolayısıyla izledikleri sırayı çözebilirsek, tüm çarpmaları yapmamıza gerek kalmadan herhangi bir kuvveti hesaplayabileceğiz.

Bu, tüm kuvvetleri hesaplamak zorunda kalmadan bize bir matrisin n’inci kuvvetini veren bir formül bulabileceğimiz anlamına gelir.

Güçlerin takip ettiği modeli keşfetmeye yönelik ipuçları :

Üssün paritesi . Çift güçler bir yönde, tek güçler ise diğer yönde olabilir.
İşaretlerin çeşitliliği. Örneğin, çift güçlerin unsurları pozitif, tek güçlerin unsurları negatif olabilir veya tam tersi olabilir.
Tekrarlama: Aynı matrisin her belirli sayıda tekrarlanıp tekrarlanmaması.
Üs ile matrisin elemanları arasında bir ilişki olup olmadığına da bakmalıyız.

Bir matrisin n kuvvetinin hesaplanmasına örnek:

Olmak
$A$

aşağıdaki matrisi hesaplayın

$A^n$

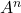
Ve

$A^{100}$

.

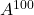
$\displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}$

İlk önce matrisin birkaç kuvvetini hesaplayacağız

$A$

, güçlerin takip ettiği modeli tahmin etmeye çalışmak. Yani hesaplıyoruz

$A^2$

$A^3$

$A^4$

$A^5:$

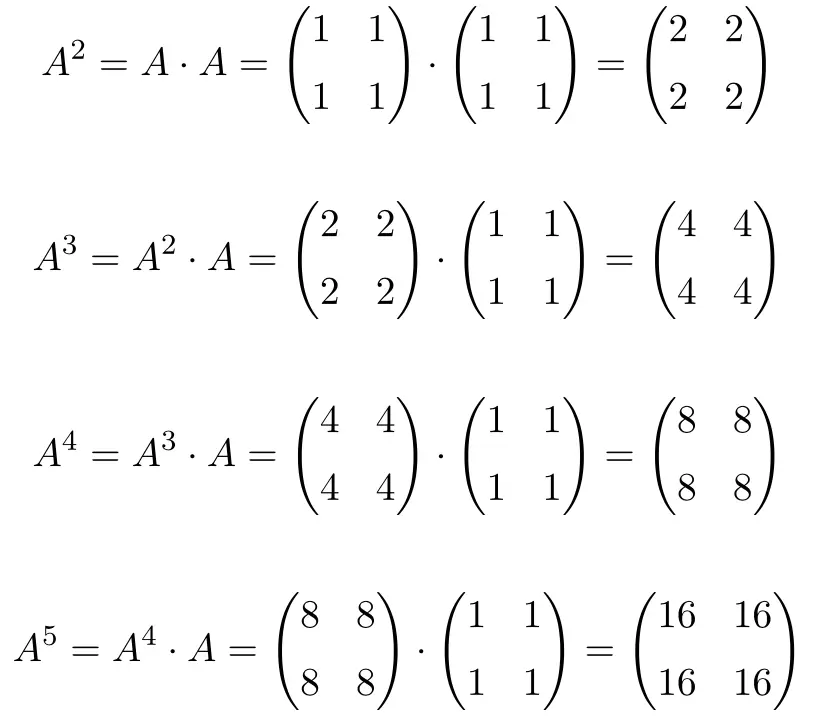
2x2 matrislerin kuvvetlerinin adım adım çözülmesi alıştırması

kadar hesaplanırken

$A^5$

matrisin kuvvetlerinin olduğunu görüyoruz

$A$

Bir kalıp izlerler: Güçteki her artış için sonuç 2 ile çarpılır. Bu nedenle tüm matrisler 2’nin kuvvetleridir:

$\displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}$

$\displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}$

$\displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}$

$\displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}$

Bu nedenle matrisin n’inci kuvvetinin formülünü elde edebiliriz.

$A:$

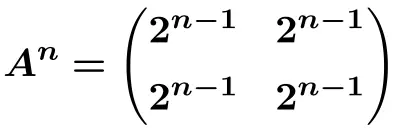
Ve bu formülden hesaplayabiliriz

$A^{100}:$

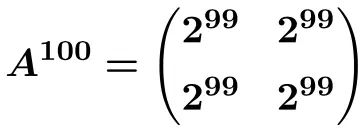
egzersiz 2x2'lik bir matrisin adım adım kuvvetini çözdü

Çözülmüş matris güç problemleri

1. Egzersiz

Aşağıdaki 2×2 boyut matrisini göz önünde bulundurun:

$\displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}$

Hesaplamak:

$\displaystyle A^4$

Çözüme bakın

Bir matrisin kuvvetini hesaplamak için matrisi birer birer çarpmanız gerekir. Bu nedenle ilk önce hesaplıyoruz

$\displaystyle A^2 :$

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}$

Şimdi hesaplıyoruz

$\displaystyle A^3 :$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}$

Ve sonunda hesaplıyoruz

$\displaystyle A^4 :$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}$

Alıştırma 2

Aşağıdaki 2. dereceden matrisi düşünün:

$\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}$

Hesaplamak:

$\displaystyle A^{35}$

Çözüme bakın

$\displaystyle A^{35}$

elle hesaplanamayacak kadar büyük bir güç olduğundan matris kuvvetlerinin bir model izlemesi gerekir. O halde hadi hesaplayalım

$\displaystyle A^5$

izledikleri sırayı anlamaya çalışmak için:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}$

Bu şekilde kuvvetlerin takip ettiği modeli görebiliriz: her kuvvette, ikinci satırın ikinci sütunundaki 3 ile çarpılan eleman dışında tüm sayılar aynı kalır. Dolayısıyla tüm sayılar her zaman aynı kalır. ve son öğe 3’ün kuvvetidir:

$\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}$

$\displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}$

$\displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}$

$\displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}$

$\displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}$

Yani matrisin n’inci kuvvetinin formülü

$\displaystyle A$

Doğu:

$\displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}$

Ve bu formülden hesaplayabiliriz

$\displaystyle A^{35}:$

$\displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}$

Alıştırma 3

Aşağıdaki 3×3 matrisi göz önünde bulundurun:

$\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Hesaplamak:

$\displaystyle A^{100}$

Çözüme bakın

$\displaystyle A^{100}$

elle hesaplanamayacak kadar büyük bir güç olduğundan matris kuvvetlerinin bir model izlemesi gerekir. O halde hadi hesaplayalım

$\displaystyle A^5$

izledikleri sırayı anlamaya çalışmak için:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Bu şekilde kuvvetlerin izlediği modeli görebiliriz: her kuvvette, payda birer artan kesirler dışında tüm sayılar aynı kalır:

$\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Yani n’inci matrisin kuvvetinin formülü

$\displaystyle A$

Doğu:

$\displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Ve bu formülden hesaplayabiliriz

$\displaystyle A^{100}:$

$\displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}$

Alıştırma 4

Aşağıdaki 2×2 boyutunda matrisi düşünün:

$\displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}$

Hesaplamak:

$\displaystyle A^{201}$

Çözüme bakın

$\displaystyle A^{201}$

elle hesaplanamayacak kadar büyük bir güç olduğundan matris kuvvetlerinin bir model izlemesi gerekir. Bu durumda hesaplamak gerekir

$\displaystyle A^{8}$

Takip ettikleri sırayı bilmek için:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}$

$\displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

$\displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}$

$\displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}$

Bu hesaplamalarla her 4 kuvvetin birim matrisini elde ettiğimizi görebiliriz. Yani sonuç olarak bize güçlerin özdeşlik matrisini verecektir.

$\displaystyle A^4$

$\displaystyle A^8$

$\displaystyle A^{12}$

$\displaystyle A^{16}$

,… Yani hesaplamak için

$\displaystyle A^{201}$

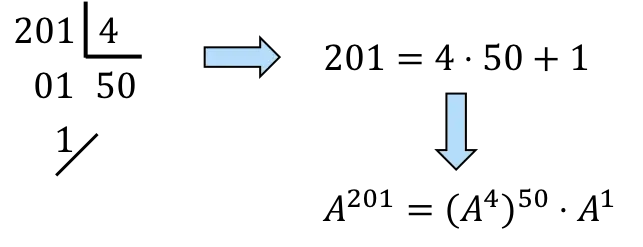
201’i 4’ün katlarına ayırmalıyız:

2x2 matrislerin kuvvetlerinin ve n kuvvetinin adım adım çözüldüğü alıştırma

$\displaystyle 201= 4 \cdot 50 +1$

,Henüz,

$A^{201}$

50 katı olacak

$\displaystyle A^{4}$

ve bir kez

$\displaystyle A^{1}:$

$\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1$

Peki bunu nasıl biliyoruz?

$\displaystyle A^4$

kimlik matrisi

$\displaystyle I :$

$\displaystyle A^4 =I$

$\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1 = I^{50}\cdot A$

Ayrıca herhangi bir sayıya yükseltilmiş birim matrisi birim matrisini verir. Henüz:

$\displaystyle A^{201}= I^{50}\cdot A = I \cdot A$

Ve son olarak, herhangi bir matris birim matrisle çarpıldığında aynı matrisi verir. BU YÜZDEN:

$\displaystyle A^{201}= I \cdot A = A$

Ne için

$A^{201}$

eşittir

$A:$

$\displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Alıştırma 5

Aşağıdaki 3. dereceden matrisi düşünün:

$\displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}$

Hesaplamak:

$\displaystyle A^{62}$

Çözüme bakın

Açıkçası, matrisin gücünü hesaplayın

$\displaystyle A^{62}$

Bu elle yapılamayacak kadar büyük bir hesaplamadır, dolayısıyla matris kuvvetlerinin bir model izlemesi gerekir. Bu durumda hesaplamak gerekir

$\displaystyle A^{6}$

Takip ettikleri sırayı bilmek için:

$\displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}$

$\displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Bu hesaplamalarla her 3 kuvvetin birim matrisini elde ettiğimizi görebiliriz. Yani sonuç olarak bize güçlerin özdeşlik matrisini verecektir.

$\displaystyle A^3$

$\displaystyle A^6$

$\displaystyle A^{9}$

$\displaystyle A^{12}$

,… Böylece hesaplamak için

$\displaystyle A^{62}$

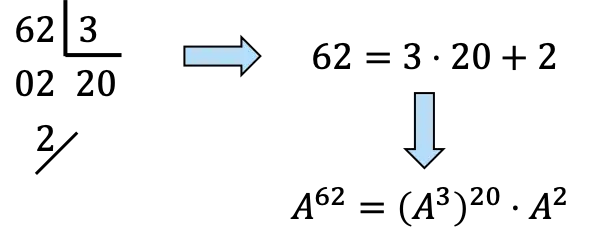
62’yi 3’ün katlarına ayırmalıyız:

3x3'lük bir matrisin n'inci kuvvetinin adım adım çözülmesi egzersizi

$\displaystyle 62= 3 \cdot 20 +2$

,Henüz,

$\displaystyle A^{62}$

20 katı olacak

$\displaystyle A^{3}$

ve bir kez

$\displaystyle A^{2}:$

$\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2$

Peki bunu nasıl biliyoruz?

$\displaystyle A^3$

kimlik matrisi

$\displaystyle I :$

$\displaystyle A^3 =I$

$\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2 = I^{20}\cdot A^2$

Ayrıca herhangi bir sayıya yükseltilmiş birim matrisi birim matrisini verir. Henüz:

$\displaystyle A^{62}= I^{20}\cdot A^2 = I \cdot A^2$

Son olarak herhangi bir matris birim matrisle çarpıldığında aynı matris elde edilir. Henüz:

$\displaystyle A^{62}= I \cdot A^2 = A^2$

Ne için

$A^{62}$

eşit olacak

$A^{2}$

sonucunu daha önce hesapladığımız için:

$\displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}$

Kare matrislerin kuvvetleriyle ilgili bu alıştırmalar işinize yaradıysa, matrislerle en çok kullanılan işlemlerden biri olan matrislerin toplanması ve çıkarılmasıyla ilgili adım adım çözülmüş alıştırmalar da bulabilirsiniz.

Bir matrisin gücü nasıl hesaplanır?

Bir matrisin gücünün hesaplanmasına örnek:

Bir matrisin kuvveti n nedir?

Bir matrisin n kuvvetinin hesaplanmasına örnek:

Çözülmüş matris güç problemleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et