Les systèmes d’équations sont des ensembles de deux équations ou plus qui ont plus d’une inconnue. Ainsi, pour résoudre des systèmes, nous pouvons utiliser quatre méthodes : la substitution, l’égalisation, la réduction et la représentation graphique. Mais, avant de commencer à expliquer les procédures de résolution, nous allons définir les types de systèmes qui existent en fonction du nombre de solutions :
- Système compatible déterminé : il n’a qu’une seule solution et on peut la représenter par deux droites qui se coupent en un seul point (qui est la solution).
- Système compatible indéterminé : il a des solutions infinies et cela est dû au fait qu’il y a deux droites qui coïncident aux mêmes points.
- Système incompatible : il n’a pas de solution, puisque les droites sont parallèles et n’ont donc aucun point commun.
Méthodes de résolution de systèmes d’équations linéaires
Nous allons maintenant expliquer les différents systèmes que nous pouvons utiliser pour résoudre des systèmes d’équations. Dans les explications, vous trouverez la théorie et quelques exemples, grâce auxquels tous les concepts expliqués seront plus clairs. A noter que dans cet article nous ne parlerons que de systèmes d’équations 2×2 , ce qui signifie que nous traiterons simplement de systèmes composés de deux équations. Cela dit, commençons par l’explication.
méthode de substitution
La méthode de substitution consiste à isoler l’une des inconnues dans l’une des équations puis à substituer l’expression obtenue dans l’équation opposée. Cette méthode est la plus recommandée lorsqu’au moins une des inconnues a la valeur du coefficient égale à 1. Ainsi, les étapes à suivre sont très simples :
- Isoler une quantité inconnue de l’une des deux équations.
- Remplacez dans l’autre équation l’expression équivalente à l’inconnue que nous avons éliminée de la première équation.
- Effacez l’inconnue opposée dans l’équation que nous avons obtenue.
- Une fois que nous avons la valeur de la première variable, nous devons l’utiliser pour trouver la seconde.
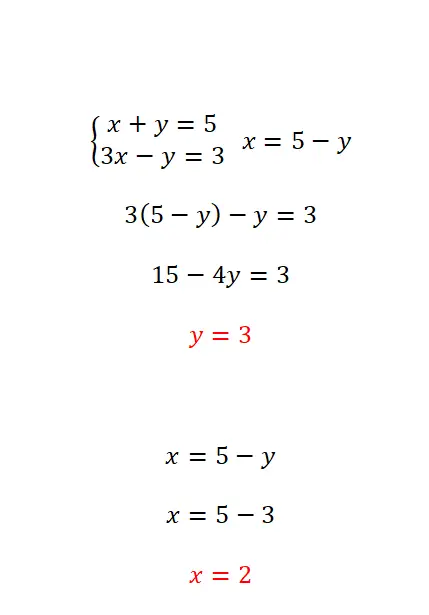
méthode d’égalisation
La méthode d’appariement consiste à isoler la même variable dans les deux équations puis à apparier les deux expressions obtenues. Cette méthode est recommandée lorsque la même inconnue peut être facilement isolée dans les deux équations, car elle facilite l’ensemble du calcul. La procédure que vous devez suivre dans ce cas est la suivante :
- Nous isolons l’inconnue que nous avons choisie dans les deux équations.
- On assimile les expressions équivalentes à cette inconnue.
- Nous résolvons l’équation normalement.
- Nous calculons l’autre inconnue avec la valeur que nous avons calculée.
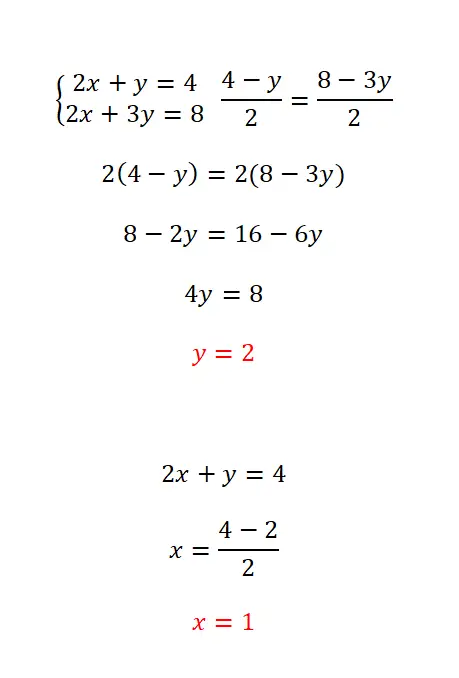
méthode de réduction
La méthode de réduction est basée sur la multiplication des deux équations par deux nombres, ce qui nous permet d’obtenir le même coefficient avec un signe différent de l’une des variables dans les deux expressions. Cette méthode est la plus recommandée lorsque la même inconnue a le même coefficient dans toutes les équations ou dans le cas d’avoir les mêmes coefficients de signes opposés. Et la procédure de résolution est la suivante :
- Les deux équations sont multipliées par les nombres nécessaires (il faut trouver deux nombres qui permettent d’obtenir le même coefficient pour l’une des deux variables dans les deux équations, mais de signe opposé).
- Ensuite, les équations sont soustraites ou additionnées pour éliminer cette inconnue avec leurs coefficients respectifs.
- Ensuite, l’équation restante est résolue.
- Et nous utilisons le résultat de cette équation pour obtenir la valeur numérique qui nous manque dans l’autre variable.
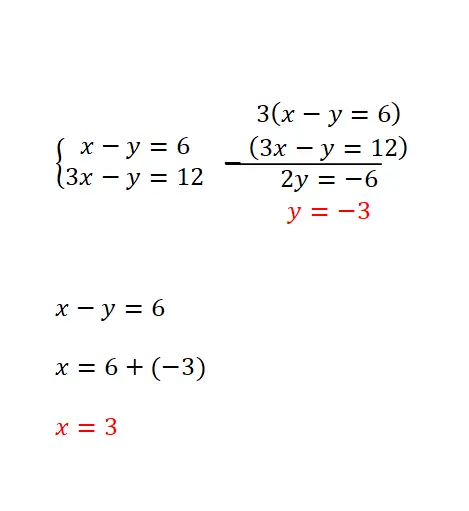
méthode graphique
Enfin, nous pouvons choisir de résoudre un système d’équations au moyen d’ une représentation graphique . Cette méthode est assez différente des autres, car elle n’a pas de partie mathématique complexe, elle est presque entièrement graphique. Ainsi, pour connaître les valeurs des inconnues, nous devons structurer les deux équations sous la forme de l’équation de la droite : y = mx + b . De cette manière nous pourrons faire la représentation puis, nous associerons les valeurs des coordonnées du point de coupure entre les deux fonctions aux inconnues. Voici un exemple travaillé :
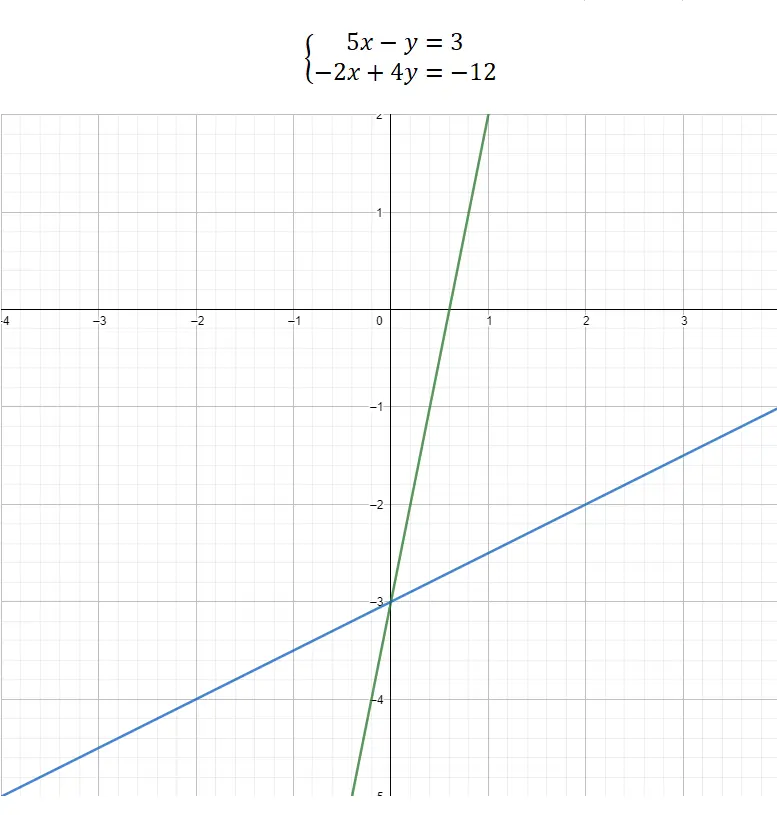
Comme on peut le voir sur le graphique, le point limite entre les deux fonctions est (0, -3). Par conséquent, la valeur de x = 0 et la valeur de y = -3. C’est ainsi qu’un système d’équations est résolu graphiquement.
Comment résoudre un système d’équations quadratiques ?
Pour résoudre des systèmes d’équations quadratiques, nous pouvons utiliser les méthodes que nous venons de discuter. Personnellement, nous aimons recommander la méthode de substitution, car elle nous permet d’obtenir rapidement une équation à une seule inconnue. Par contre, si on utilise les méthodes de réduction ou d’égalisation, le calcul devient assez compliqué. Ainsi, une fois que vous avez substitué l’une des deux variables, vous n’avez qu’à résoudre l’ équation quadratique résultante ou l’équation du premier degré . Voici un exemple pour que vous puissiez voir l’ensemble du processus :
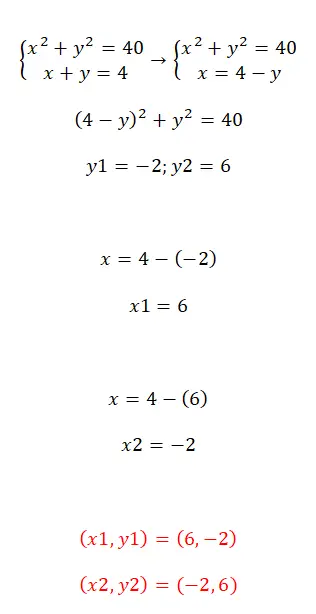
Exercices sur les systèmes d’équations résolus
Nous vous proposons maintenant quelques exercices sur les systèmes d’équations linéaires et du second degré afin que vous puissiez appliquer la théorie expliquée. De cette façon, vous comprendrez mieux tous les concepts liés au calcul des systèmes d’équations. Nous vous recommandons d’essayer de les résoudre avant de regarder les réponses que nous vous proposons, ainsi vous tirerez le meilleur parti des exercices :
Exercice 1
Résolvez ce système d’équations en utilisant la méthode de substitution :
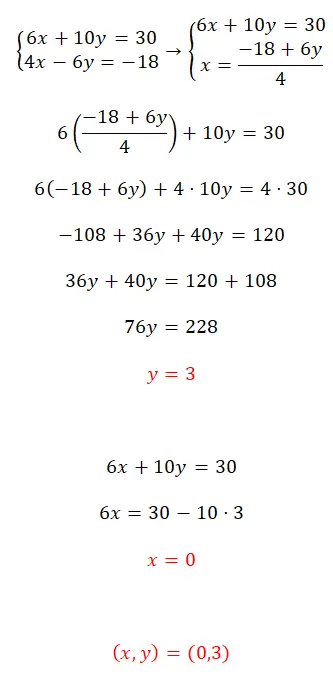
- On commence par isoler l’une des deux inconnues d’une équation.
- Puis on substitue l’expression obtenue dans l’équation ci-contre, par l’inconnue que l’on a résolu précédemment.
- On obtient alors le résultat de la variable opposée.
- Ensuite, nous substituons la première valeur découverte dans l’une des deux équations pour calculer la valeur de la première inconnue.
- Enfin, nous exprimons le résultat des deux variables.
Exercice 2
Résolvez ce système d’équations en utilisant la méthode de substitution :
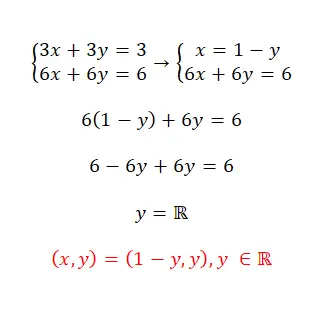
- Dans ce cas nous suivrons la même procédure : isoler une inconnue, la substituer dans l’autre expression et isoler la seconde variable.
- Comme on peut le voir, il s’agit d’un système compatible indéterminé, car il a une infinité de solutions.
Exercice 3
Résolvez ce système d’équations en utilisant la méthode d’égalisation :
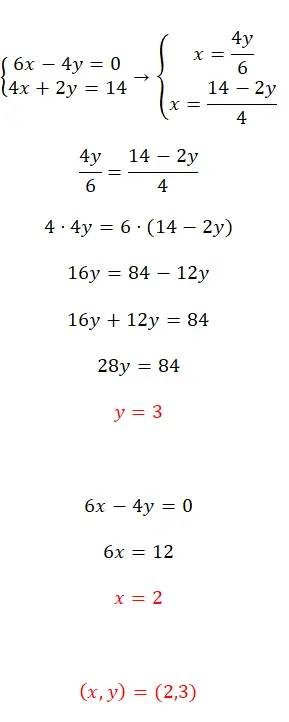
- La première étape consiste à isoler la même variable dans les deux équations, dans ce cas nous avons choisi x.
- Ensuite, nous faisons correspondre les expressions obtenues et commençons à résoudre.
- Ainsi, nous obtenons la valeur de la première inconnue.
- Et si nous la substituons dans l’une des deux équations d’origine, nous pouvons calculer la seconde inconnue.
- Enfin, nous exprimons le résultat des deux variables.
Exercice 4
Résolvez ce système d’équations en utilisant la méthode d’égalisation :
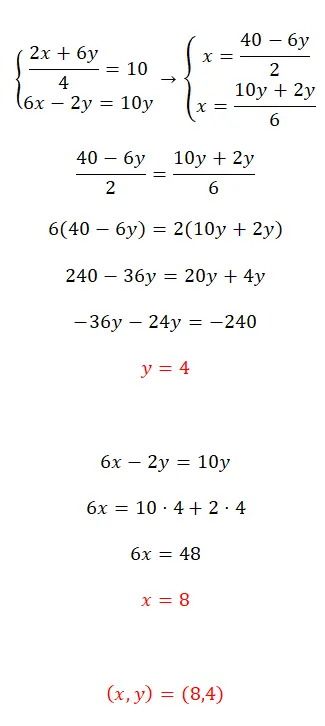
- Tout d’abord, nous isolons le x dans les deux équations.
- Ensuite, nous faisons correspondre les expressions que nous avons obtenues.
- On obtient la valeur de la première inconnue.
- Nous substituons cette valeur dans l’une des deux équations initiales et calculons la seconde inconnue.
- Enfin, nous exprimons la valeur des deux inconnues.
Exercice 5
Résolvez ce système d’équations en utilisant la méthode de réduction :
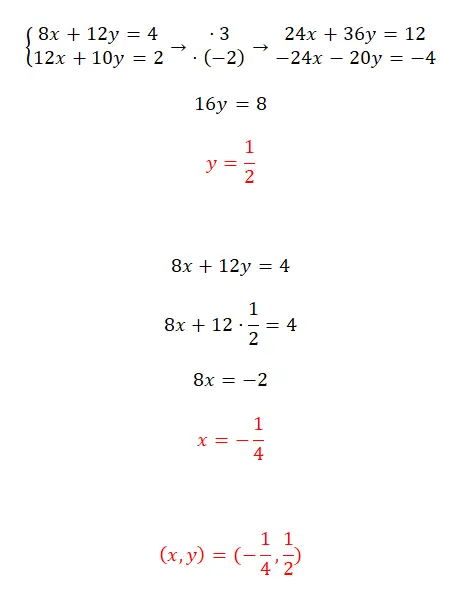
- Il faut chercher deux nombres qui permettent d’obtenir le même coefficient pour l’une des deux variables dans les deux équations, mais de signe opposé .
- Ensuite, il suffit de résoudre l’équation que l’on obtient en additionnant les deux expressions obtenues.
- Ensuite, nous substituons le y dans l’une des deux équations initiales, pour calculer le x.
- Enfin, nous exprimons le résultat du système.
Exercice 6
Résolvez ce système d’équations en utilisant la méthode de réduction :
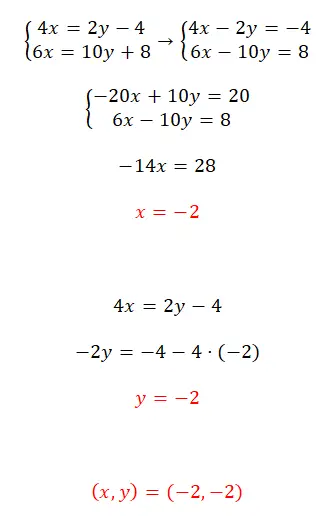
- On commence par arranger les équations (en passant toutes les variables à gauche).
- Puis on multiplie par -5 la première équation.
- Nous résolvons l’équation que nous obtenons en additionnant les deux équations et obtenons la valeur de x.
- Nous utilisons cette valeur connue pour obtenir la valeur de y.
- On exprime le résultat du système d’équations.
Exercice 7
Résolvez ce système d’équations en utilisant la méthode de substitution :
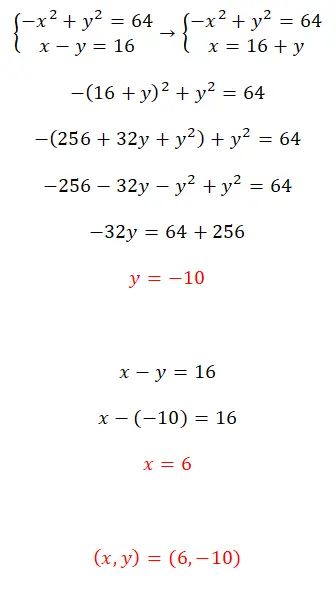
- Pour résoudre ce système d’équations non linéaires, nous vous recommandons d’utiliser la méthode de substitution.
- Donc, vous construisez une équation avec l’expression équivalente à x.
- Vous obtenez la valeur de l’inconnue y.
- Vous calculez la valeur de x avec la valeur que vous avez calculée précédemment.
- Et vous avez déjà les deux valeurs.
Exercice 8
Résolvez ce système d’équations en utilisant la méthode de votre choix :
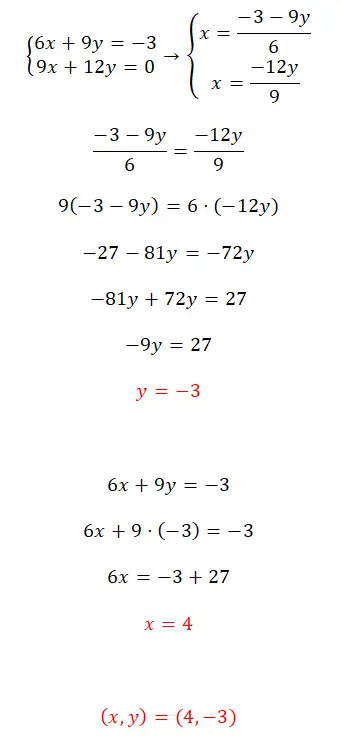
- Dans ce cas, on nous présente un système compatible déterminé et nous allons le résoudre par la méthode d’égalisation.
- Par conséquent, nous résolvons pour x dans les deux équations et définissons les deux expressions résultantes égales.
- Après avoir résolu l’équation, nous obtenons la valeur de y.
- Nous utilisons cette valeur pour trouver la valeur de x.
- Enfin, nous exprimons le résultat du système.