Système de coordonnées

Sur cette page, nous expliquons ce qu’est un système de coordonnées et, en plus, vous trouverez tout sur le système de coordonnées cartésien. Vous verrez également d’autres types de systèmes de coordonnées (polaires, cylindriques, sphériques,…) et les applications réelles d’un système de coordonnées.

Qu’est-ce qu’un système de coordonnées ?

Bien qu’il soit un peu difficile de saisir ce concept au début, la définition d’un système de coordonnées est la suivante :

Un système de coordonnées est un système qui nous permet d’identifier la position d’un point. C’est-à-dire qu’il s’agit d’un ensemble de valeurs utilisées pour définir l’emplacement de tout objet géométrique.

Par exemple, la position dans laquelle vole l’avion suivant peut être décrite par un système de coordonnées :

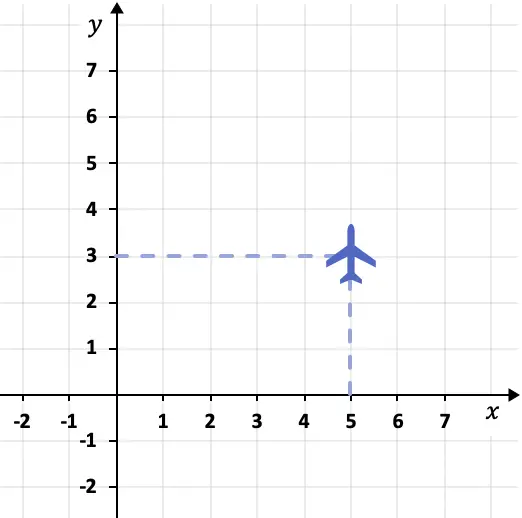
Dans ce cas, le plan est au point (5,3). Parce que sa coordonnée X est 5 et sa coordonnée Y est 3.

D’autre part, le point (0,0) est appelé l’ origine des coordonnées , car c’est là que commencent les axes de coordonnées et c’est le point de référence du système de coordonnées.

Par curiosité, on considère que le mathématicien qui a inventé le système de coordonnées était le français René Descartes. Et c’est pourquoi on l’appelle aussi système de coordonnées cartésien.

Système de coordonnées cartésiennes dans le plan

Le graphe que nous avons vu dans la section précédente appartient au repère cartésien dans le plan. On dit qu’il est dans le plan car c’est un système à deux dimensions, c’est-à-dire qu’il n’a que deux axes : l’axe X et l’axe Y.

L’axe X correspond aux coordonnées horizontales, tandis que l’axe Y représente les coordonnées verticales. Ci-dessous vous pouvez voir plusieurs points représentés graphiquement avec leurs coordonnées :

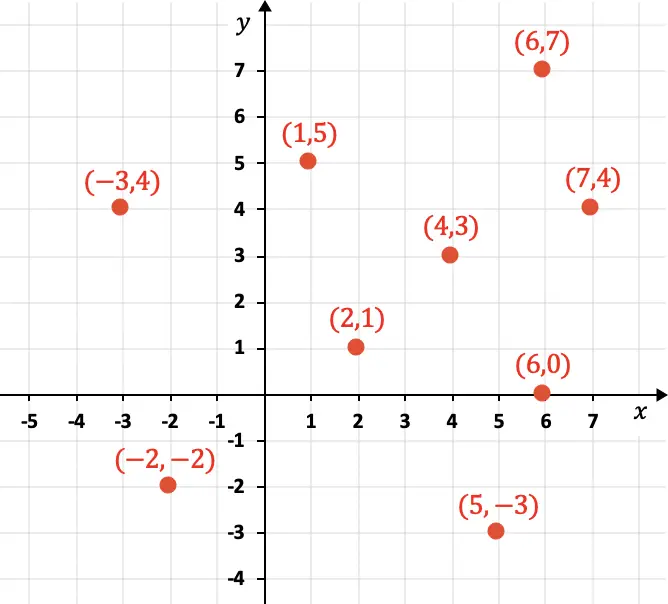
Comme vous pouvez le voir sur le graphique, les coordonnées sont représentées numériquement avec des parenthèses, de plus, la composante X est mise en premier puis la composante Y : (4,3). De plus, les coordonnées peuvent être positives, négatives ou nulles.

D’autre part, ce type de système de coordonnées est également appelé plan cartésien.

Enfin, il faut savoir que les axes de coordonnées peuvent se dire de plusieurs manières, bien qu’ils signifient tous la même chose :

• L’axe X est aussi appelé axe des abscisses ou axe OX.
• L’axe Y est également appelé axe des ordonnées ou axe OY.

Système de coordonnées cartésiennes dans l’espace

Nous venons de voir comment représenter un point dans le plan, c’est-à-dire dans un repère à deux axes (2 dimensions). Or, la réalité est composée de 3 dimensions (hauteur, largeur et profondeur).

Ainsi, en géométrie euclidienne, l’espace tridimensionnel est généralement représenté par un système de coordonnées à trois axes, tous perpendiculaires les uns aux autres :

• L’axe X représente la profondeur.
• L’axe Y indique la largeur.
• L’axe Z correspond à la hauteur.

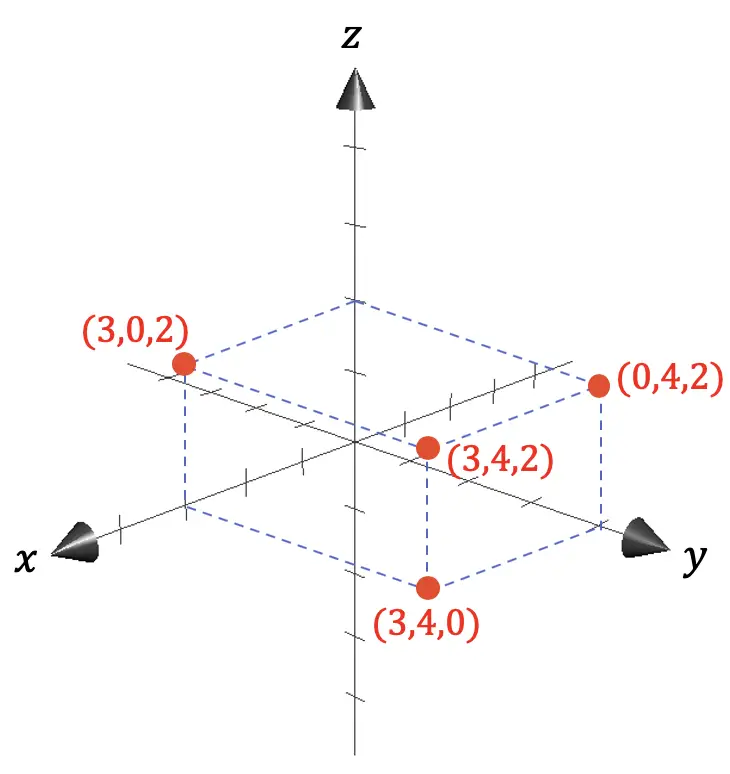
Comme vous pouvez le voir dans la représentation graphique précédente, les coordonnées de tout point sont données par les projections sur les axes des distances entre le point en question et l’origine (0,0,0).

système de coordonnées polaires

Les systèmes de coordonnées cartésiennes, 2D ou 3D, sont les plus largement utilisés. Mais à certaines occasions, il peut être pratique pour nous d’utiliser un autre type de système de coordonnées.

Le système de coordonnées polaires est un système de référence bidimensionnel dont les coordonnées sont :

• est la distance entre l’origine des coordonnées et le point. C’est ce qu’on appelle la coordonnée radiale.
• est l’angle que fait l’axe X avec la ligne passant par le point et l’origine. C’est ce qu’on appelle une coordonnée angulaire ou azimutale.

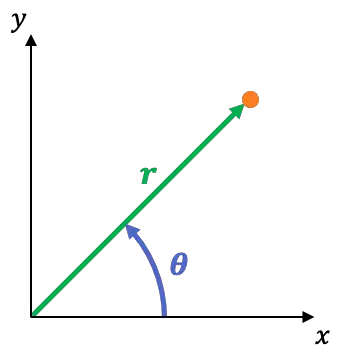
Vous pouvez facilement passer du système de coordonnées rectangulaires au système de coordonnées polaires en utilisant les équations suivantes :

Système de coordonnées cylindriques

Le système de coordonnées cylindriques est très similaire au système de coordonnées polaires. En fait, c’est la même chose mais avec une coordonnée en plus : la hauteur.

Le repère cylindrique est donc un repère tridimensionnel, c’est-à-dire à 3 coordonnées :

• est la projection orthogonale du point dans le plan XY, ou en d’autres termes, la distance du point à l’axe Z.
• est l’angle que fait le demi-axe positif X avec la droite
• est la hauteur du point, est la même coordonnée du système de coordonnées cartésiennes dans l’espace.

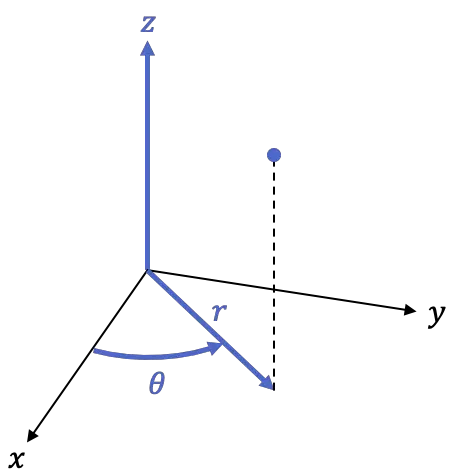
Les formules suivantes sont utilisées pour transformer le système de coordonnées cartésiennes en coordonnées cylindriques :

Système de coordonnées sphériques

Enfin, nous avons le système de coordonnées sphériques. Ce type de système de coordonnées est également assez similaire aux coordonnées polaires et aux coordonnées cylindriques, bien qu’il présente évidemment quelques différences par rapport à celles-ci.

Le système de coordonnées sphériques est un système pour décrire les espaces euclidiens tridimensionnels, par conséquent, il a trois coordonnées :

• est la distance (en R3) de l’origine au point.
• est l’angle que fait la partie positive de l’axe X avec la droite projeté dans le plan XY.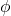
• est l’angle entre la partie positive de l’axe Z et la droite

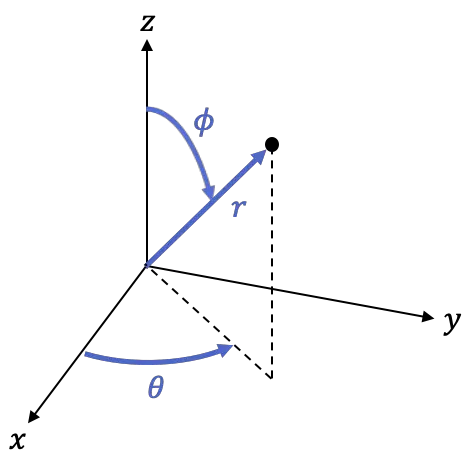
Vous pouvez basculer entre les coordonnées sphériques et cartésiennes à l’aide des formules suivantes :

Applications réelles du système de coordonnées

Les systèmes de coordonnées sont si importants en mathématiques parce qu’ils sont également utilisés dans la vie réelle. Par exemple, ils sont utiles pour localiser des objets, des personnes ou même des lieux sur une carte. En fait, le GPS existe grâce aux systèmes de coordonnées, puisque c’est ce qu’ils utilisent pour connaître votre position sur Terre.

Plus précisément, les coordonnées géographiques du GPS sont constituées de deux éléments : la latitude et la longitude. La latitude (nord ou sud) et la longitude (est ou ouest) sont deux coordonnées angulaires qui mesurent l’angle entre le centre de la Terre et votre position. Les deux sont exprimés en degrés, soit en coordonnées décimales, soit en coordonnées sexagésimales.