Ajout de vecteur

Cette page explique comment ajouter deux vecteurs dans le plan, à la fois graphiquement et numériquement. Il existe 3 façons de les ajouter graphiquement : la méthode du parallélogramme, de la tête-à-queue et du polygone. De plus, vous trouverez également des exercices résolus sur l’addition vectorielle et toutes les propriétés de l’addition vectorielle.

Comment additionner graphiquement deux vecteurs ?

Fondamentalement, il existe deux façons d’ajouter des vecteurs à partir de leur représentation graphique. Avec les deux formes, le même résultat est obtenu, mais certains préfèrent les ajouter en utilisant la méthode tête-queue et d’autres avec la méthode du parallélogramme . Nous allons donc vous expliquer les deux méthodes pour que vous choisissiez celle que vous préférez. 😉

Par contre, ces deux méthodes servent à additionner deux vecteurs, mais que se passe-t-il si on veut additionner plus de deux vecteurs ? Il faut donc utiliser la méthode du polygone , qui consiste à utiliser successivement la méthode du parallélogramme. Vous trouverez également son explication après les méthodes tête-queue et parallélogramme.

Méthode ou règle du parallélogramme

La règle du parallélogramme ou méthode du parallélogramme (ou encore loi du parallélogramme) est une procédure graphique qui permet de trouver la somme de deux vecteurs de manière très simple. Les étapes à suivre pour appliquer ce processus sont les suivantes :

1. Premièrement, nous dessinons les vecteurs et les positionnons au même point d’application, c’est-à-dire que nous plaçons les origines des deux vecteurs au même point.
2. Ensuite, nous traçons à la fin d’un vecteur une ligne parallèle à l’autre vecteur. Et nous répétons l’étape avec l’autre vecteur. On obtiendra donc le dessin d’un parallélogramme (d’où le nom de la règle).
3. Enfin, le résultat de la somme sera le vecteur qui va de l’origine commune au point où les deux droites parallèles se croisent.

Regardez l’exemple générique suivant dans lequel deux vecteurs sont ajoutés avec la règle du parallélogramme :

Le résultat de la somme des vecteurs est la diagonale du parallélogramme qu’ils forment avec leurs parallèles.

méthode tête et queue

La méthode de la tête et de la queue , ou également connue sous le nom de méthode du triangle , est une autre procédure avec laquelle deux vecteurs peuvent être ajoutés graphiquement. Dans ce cas, les étapes à suivre sont :

1. Déplacez un vecteur ajouté et placez-le de manière à ce que son origine soit juste à la fin de l’autre vecteur ajouté.
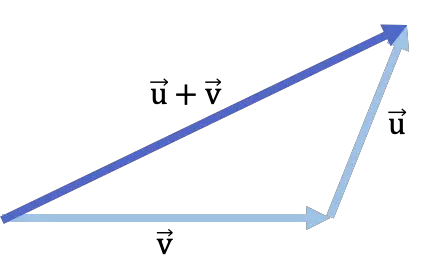
2. Le résultat de l’addition vectorielle est le segment qui va du début du premier vecteur ajouté à la fin de l’autre vecteur. Si vous regardez bien, un triangle se complète avec les deux vecteurs ajoutés et le vecteur ajouté.

Voici un exemple d’addition vectorielle avec la méthode tête-bêche :

méthode du polygone

Une fois que nous avons vu comment résoudre graphiquement la somme de deux vecteurs, nous allons voir comment cela se fait lorsque nous avons plus de deux vecteurs.

Lorsque l’on veut additionner trois vecteurs ou plus, il existe une technique pour aller plus vite dans le calcul de l’opération. Cette technique est appelée méthode du polygone et consiste à appliquer successivement la méthode tête-bêche :

1. Nous devons d’abord placer chaque vecteur après l’autre, de sorte que l’origine d’un vecteur coïncide avec la fin d’un autre vecteur. L’ordre dans lequel nous les plaçons est indifférent.
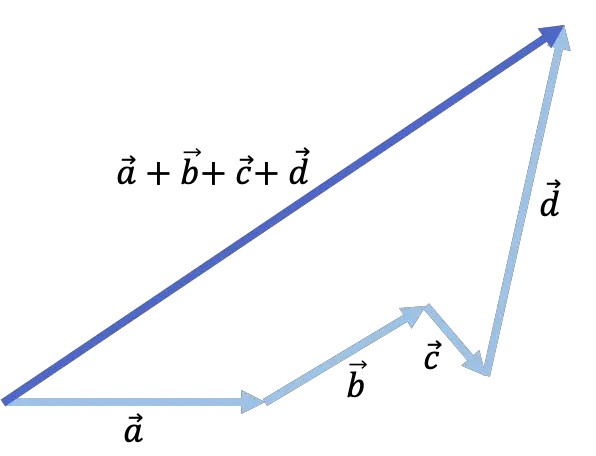
2. Et le résultat de la somme est le vecteur obtenu en joignant le début du premier vecteur à la fin du dernier vecteur.

Regardez l’exemple suivant où 4 vecteurs sont ajoutés :

Calculer numériquement la somme de deux vecteurs

Une fois que l’on sait additionner des vecteurs géométriquement, on va voir comment calculer numériquement ou algébriquement une somme vectorielle.

Par exemple, la somme entre les vecteurs

et est:

D’autre part, il faut garder à l’esprit que l’addition vectorielle de deux vecteurs n’est pas la même chose que l’addition des modules des vecteurs, en fait, les résultats sont totalement différents. Vous pouvez voir les différences entre les deux opérations dans les propriétés de la magnitude d’un vecteur (également appelée magnitude d’un vecteur).

Propriétés d’ajout de vecteur

L’addition vectorielle a les caractéristiques suivantes :

• Propriété associative : Mettre des parenthèses entre la somme de plusieurs vecteurs ne modifie pas le résultat de l’opération.

• Propriété commutative – Contrairement à la soustraction vectorielle, le résultat de l’addition entre deux vecteurs est indépendant de l’ordre dans lequel ils sont ajoutés.

• Propriété de l’élément opposé : la somme d’un vecteur plus son opposé, c’est-à-dire sa négation, est égale à 0.

• Propriété de l’élément neutre : évidemment, tout vecteur plus le vecteur nul ou nul est équivalent au vecteur lui-même :

Problèmes résolus d’addition de vecteurs

Exercice 1

Calculer graphiquement la somme des vecteurs

et

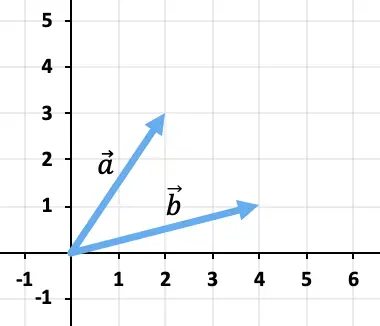
Pour additionner les deux vecteurs, nous utiliserons la règle de la tête et de la queue. On placera donc l’origine du vecteur

à la fin du vecteur , et la somme sera le vecteur qui va de l’origine des coordonnées à la fin de

Par conséquent, le résultat de l’addition vectorielle est :

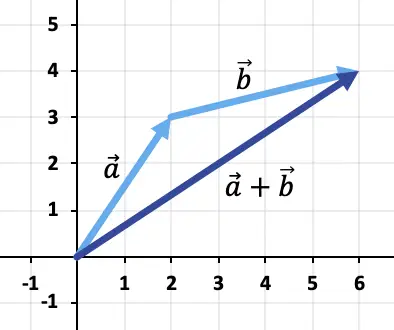
Exercice 2

Résoudre graphiquement la somme des vecteurs

et

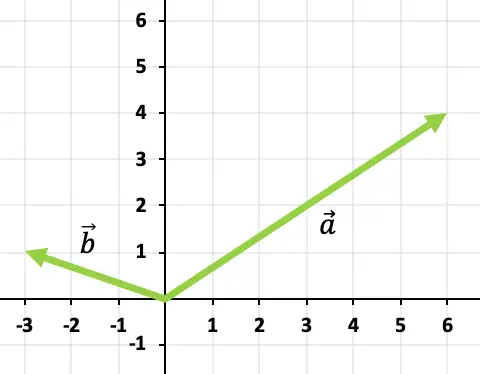
Pour additionner les deux vecteurs, nous utiliserons la règle tête-queue. Nous allons donc localiser l’origine du vecteur

à la fin du vecteur , et le vecteur somme sera celui qui va de l’origine des axes à la fin de

Par conséquent, le résultat de l’addition vectorielle est :

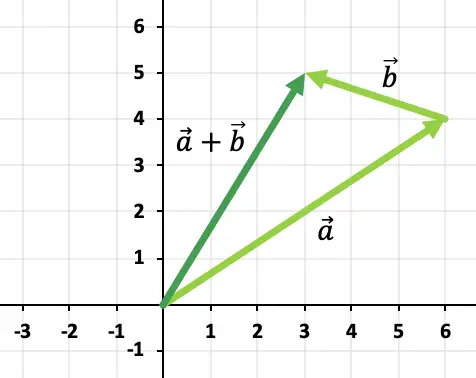
Exercice 3

Déterminer graphiquement le vecteur résultant de l’addition de tous les vecteurs représentés dans le graphe :

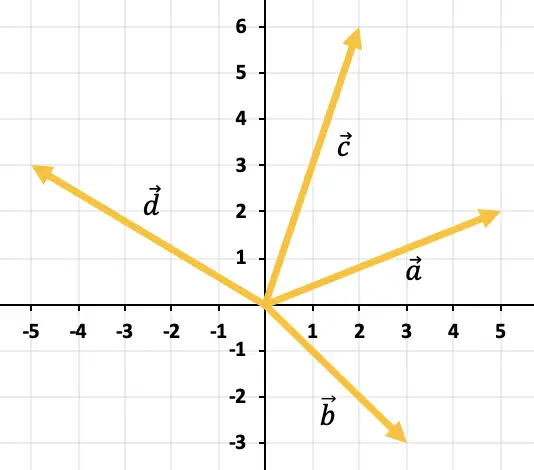
Pour ajouter plus de 2 vecteurs à partir du graphique, vous devez utiliser la règle du polygone. Il faut donc déplacer les vecteurs pour qu’ils restent continus, c’est-à-dire les uns après les autres (l’ordre est indifférent). Ainsi, la somme de tous les vecteurs sera le vecteur qui va de l’origine du premier vecteur à la fin du dernier vecteur.

Donc le résultat de la somme des 4 vecteurs est le vecteur représenté en rouge :

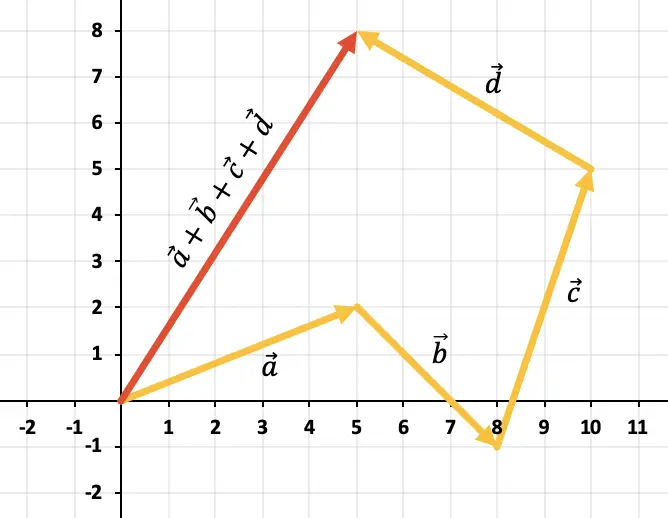
Exercice 4

Trouvez numériquement la somme des vecteurs suivants :

Pour additionner numériquement deux vecteurs il faut additionner leurs coordonnées respectives :

Exercice 5

Calculez analytiquement la somme des vecteurs suivants :

Pour additionner numériquement des vecteurs il faut additionner leurs coordonnées respectives :