Sur cette page, vous trouverez la définition des sections coniques, pourquoi elles sont si importantes et les différents types de sections coniques qui existent (cercle, ellipse, hyperbole et parabole). De plus, vous pourrez voir les différences entre leurs équations.
Que sont les sections coniques ?
En géométrie analytique, les sections coniques (ou simplement coniques) sont toutes les courbes résultant des différentes intersections entre un cône et un plan, lorsque ce plan ne passe pas par le sommet du cône. Il existe quatre types de sections coniques : le cercle, l’ellipse, la parabole et l’hyperbole.
Vous trouverez ci-dessous les 4 sections possibles pouvant être obtenues à partir de n’importe quel cône :
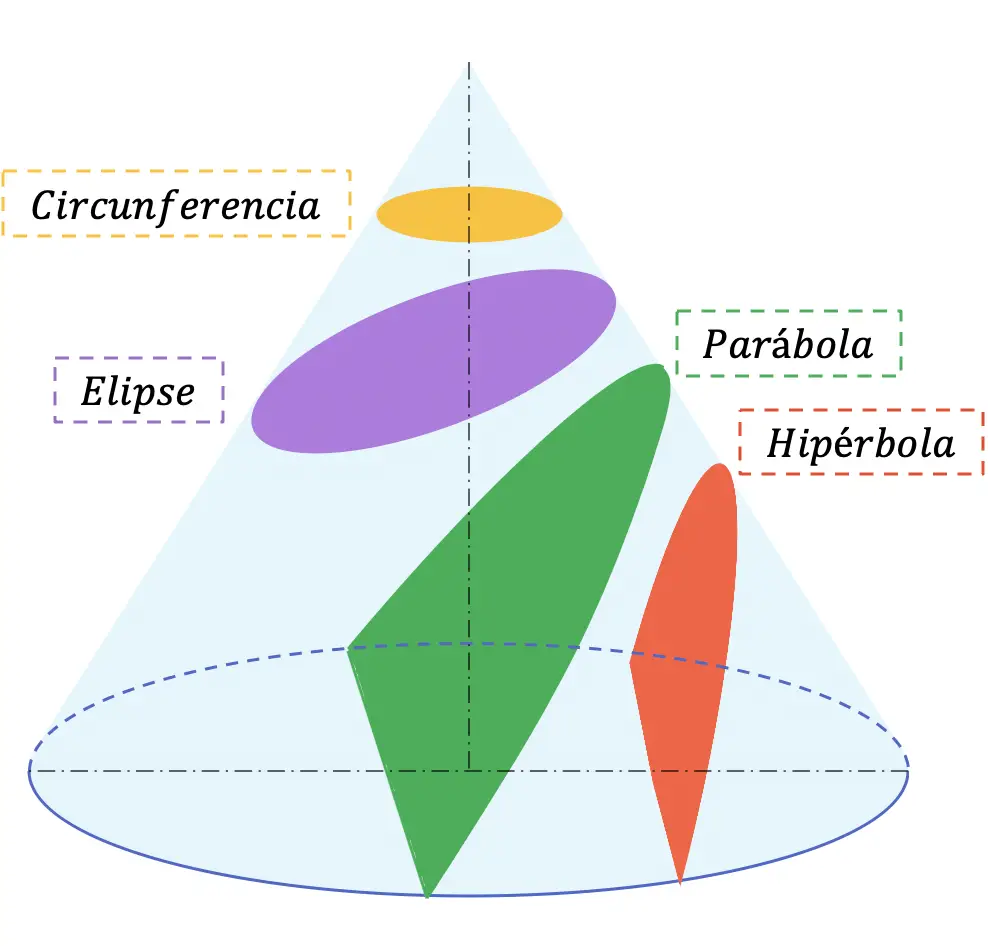
Les sections coniques sont généralement étudiées au secondaire (Bachillerato), dans les matières de mathématiques et de dessin technique.
Types de sections coniques
Une fois que nous avons vu le concept de section conique, voyons quels sont les quatre types de sections coniques qui existent : le cercle, l’ellipse, la parabole et l’hyperbole.
circonférence
La circonférence est une section conique que l’on peut trouver en coupant un cône avec un plan perpendiculaire à son axe de révolution (parallèle à la base).
De plus, la circonférence est le lieu des points du plan équidistants d’un point fixe appelé centre.
Ellipse
L’ellipse est une ligne plate, fermée et incurvée très semblable à la circonférence, mais sa forme est plus ovale. En particulier, il résulte de la découpe de la surface d’un cône par un plan oblique dont l’angle par rapport à l’axe de révolution est supérieur à celui de la génératrice.
De plus, tous les points d’une ellipse vérifient une condition : l’ellipse est le lieu de tous les points d’un plan dont la somme des distances à deux autres points fixes (appelés foyers F et F’) est constante.
Parabole
En mathématiques, une parabole est le lieu des points du plan qui sont équidistants d’un point fixe (appelé le foyer) et d’une ligne fixe (appelée la directrice).
Géométriquement, la parabole est le résultat de la coupe d’un cône par un plan d’angle d’inclinaison par rapport à l’axe de révolution équivalent à l’angle de la génératrice du cône. Par conséquent, le plan contenant la parabole est parallèle à la génératrice du cône.
Une caractéristique très importante de cette section conique est l’ équation de la parabole , car selon son état, elle nous permet d’identifier de quel type de parabole il s’agit. Dans ce lien, vous trouverez toutes les équations de la parabole, quels sont les éléments de la parabole, leurs propriétés, des exemples, des exercices résolus,… entre autres caractéristiques des paraboles.
Hyperbole
En tant que section conique, une hyperbole est obtenue lorsqu’un cône est coupé par un plan d’angle inférieur à l’angle formé par la génératrice du cône par rapport à son axe de révolution.
Mathématiquement, une hyperbole peut être définie comme le lieu des points du plan qui répondent à la propriété suivante : la valeur absolue de la différence des distances entre n’importe quel point de l’hyperbole et deux points fixes (appelés foyers) doit être constante.
De plus, la valeur de la soustraction de ces deux distances est toujours équivalente à la distance entre les deux sommets de l’hyperbole.
Comme je suis sûr que vous l’avez déjà déduit, la valeur du paramètre
d’une hyperbole est fondamentale pour les hyperboles. Dans le lien suivant, vous pouvez voir notre explication de l’hyperbole, où vous trouverez pourquoi c’est un coefficient si important ainsi que quels sont tous les éléments qui caractérisent une hyperbole. De plus, vous trouverez à quoi ressemble l’ équation d’une hyperbole , les différents types d’hyperboles qui existent, et même des problèmes et exercices résolus pas à pas sur les hyperboles.
Équation générale des sections coniques
Chaque section conique peut être exprimée analytiquement sous la forme d’une équation. En fait, toutes les équations des coniques doivent être du second degré :
Par conséquent, au moins un des coefficients
soit
de la formule doit être différent de zéro.
Ainsi, selon les valeurs des paramètres, l’équation correspondra à un type de conique ou à un autre :
- Circonférence : pour l’équation générale décrivant une circonférence, les termes
et doit correspondre et
doit être nul.
- Ellipse : l’équation correspondra à l’expression mathématique d’une ellipse lorsque la condition suivante est vérifiée :
- Parabole : pour que l’équation soit une parabole, l’égalité suivante doit être remplie :
- Hyperbole : Enfin, l’équation générale d’une hyperbole doit satisfaire l’inégalité suivante :
