Якобиан и матрица Якобиана

На этой странице вы узнаете, что такое матрица Якобиана и как ее рассчитать на примере. Кроме того, у вас есть несколько решенных упражнений с матрицами Якоби, чтобы вы могли попрактиковаться. Вы также поймете, почему определитель матрицы Якобиана, якобиан, так важен. Наконец, мы объясняем отношения, которые эта матрица поддерживает с другими операциями и приложениями, которые она имеет.

Что такое матрица Якобиана?

Определение матрицы Якобиана следующее:

Матрица Якобиана — это матрица, образованная частными производными первого порядка функции.

Таким образом, формула матрицы Якобиана выглядит следующим образом:

Следовательно, матрицы Якоби всегда будут иметь столько же строк, сколько скалярные функции.

$(f_1,f_2,\ldots ,f_m)$

есть функция, а количество столбцов будет соответствовать количеству переменных

$(x_1, x_2, \ldots , x_n).$

С другой стороны, эта матрица также известна как дифференциальная карта Якоби или линейная карта Якоби . На самом деле иногда его тоже пишут буквой D вместо буквы J:

$\displaystyle J_f = D_f$

Любопытно, что матрица Якобиана названа в честь Карла Густава Якоби, выдающегося математика и профессора XIX века, внесшего важный вклад в мир математики, особенно в область линейной алгебры.

Пример расчета матрицы Якобиана

Как только мы познакомимся с понятием матрицы Якобиана, мы шаг за шагом увидим, как она рассчитывается, на примере:

Определим матрицу Якобиана в точке (1,2) следующей функции:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

Первое, что нам нужно сделать, это вычислить все частные производные первого порядка функции:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Теперь применим формулу матрицы Якобиана. В данном случае функция имеет две переменные и две скалярные функции, поэтому матрица Якобиана будет квадратной матрицей размерности 2×2:

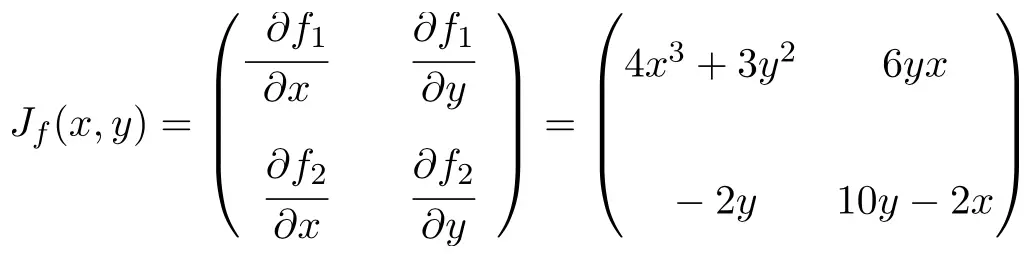
Получив выражение для матрицы Якобиана, мы оцениваем его в точке (1,2):

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

И, наконец, проводим операции и получаем решение:

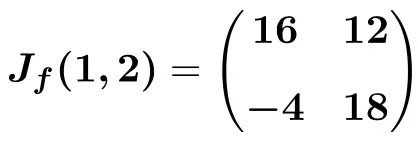
После того, как вы узнали, как найти матрицу Якобиана функции, мы оставим вам несколько упражнений, решаемых шаг за шагом, чтобы вы могли попрактиковаться.

Решенные проблемы матриц Якобиана

Упражнение 1

Найдите матрицу Якобиана в точке (0,-2) следующей вектор-функции от 2 переменных:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

посмотреть решение

Функция имеет две переменные и две скалярные функции, поэтому матрица Якобиана будет квадратной матрицей размера 2×2:

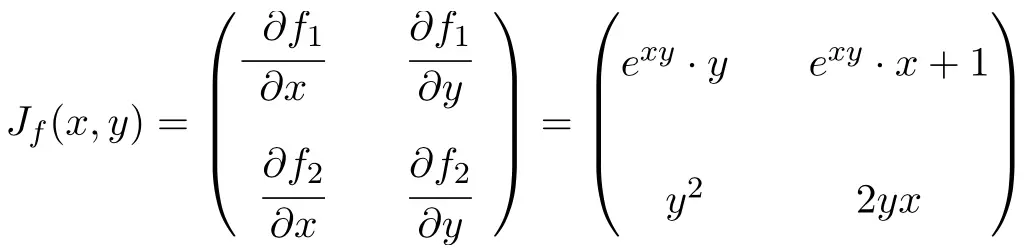
После того как мы вычислили выражение для матрицы Якобиана, мы оцениваем его в точке (0,-2):

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

И, наконец, проводим операции и получаем результат:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Упражнение 2

Вычислите матрицу Якобиана в точке (2,-1) следующей функции с двумя переменными:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

посмотреть решение

В данном случае функция имеет две переменные и две скалярные функции, поэтому матрица Якобиана будет квадратной матрицей второго порядка:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Найдя выражение для матрицы Якобиана, мы оцениваем его в точке (2,-1):

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

И, наконец, проводим операции и получаем результат:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Упражнение 3

Определите матрицу Якобиана в точке (2,-2,2) следующей функции с 3 переменными:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

посмотреть решение

В данном случае функция имеет три переменные и две скалярные функции, следовательно, матрица Якобиана будет прямоугольной матрицей размерности 2×3:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

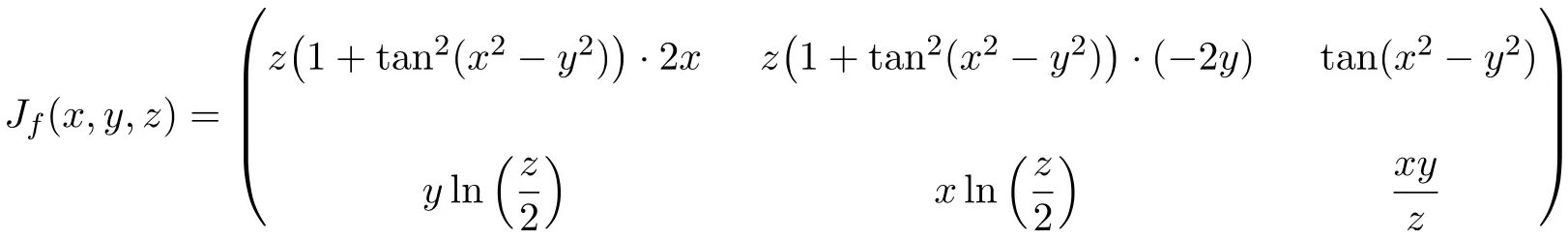
Матрица Якоби, решающее упражнение с 3 переменными

Получив выражение для матрицы Якобиана, мы оцениваем его в точке (2,-2,2):

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Проводим расчеты:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

И продолжаем действовать до тех пор, пока его уже нельзя будет упростить:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Упражнение 4

Определить матрицу Якобиана в точке

$(\pi, \pi)$

следующей функции многих переменных:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

посмотреть решение

В данном случае функция имеет две переменные и три скалярные функции, следовательно, матрица Якобиана будет прямоугольной матрицей размерности 3×2:

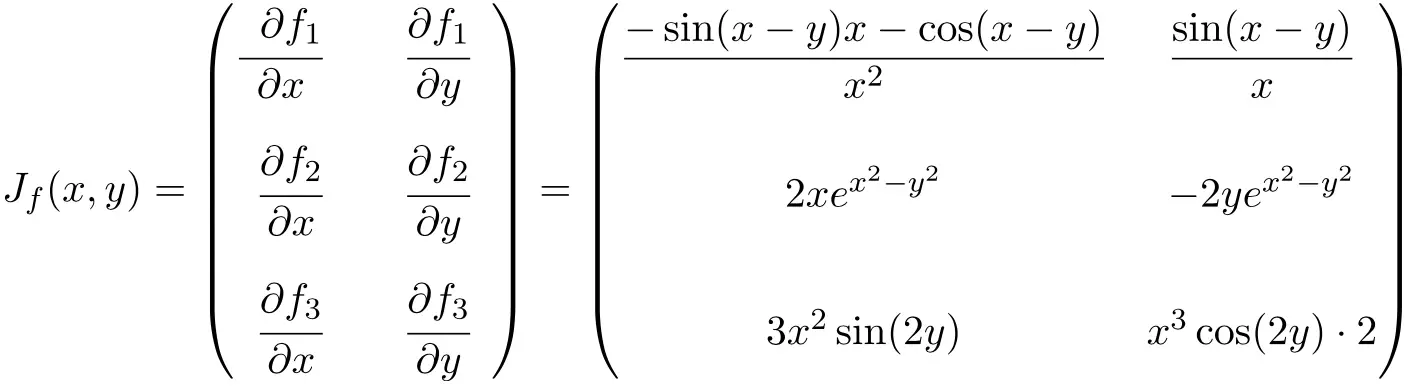
упражнение пошагово решает матрицу Якобиана

Получив выражение для матрицы Якобиана, мы оцениваем его до точки

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Мы выполняем операции:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

Таким образом, матрица Якоби векторной функции в рассматриваемой точке имеет вид:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Упражнение 5

Вычислить матрицу Якобиана в точке

$(3,0,\pi)$

следующей функции с тремя переменными:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

посмотреть решение

В данном случае функция имеет три переменных и три скалярные функции, следовательно, матрица Якобиана будет квадратной матрицей размерности 3×3:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

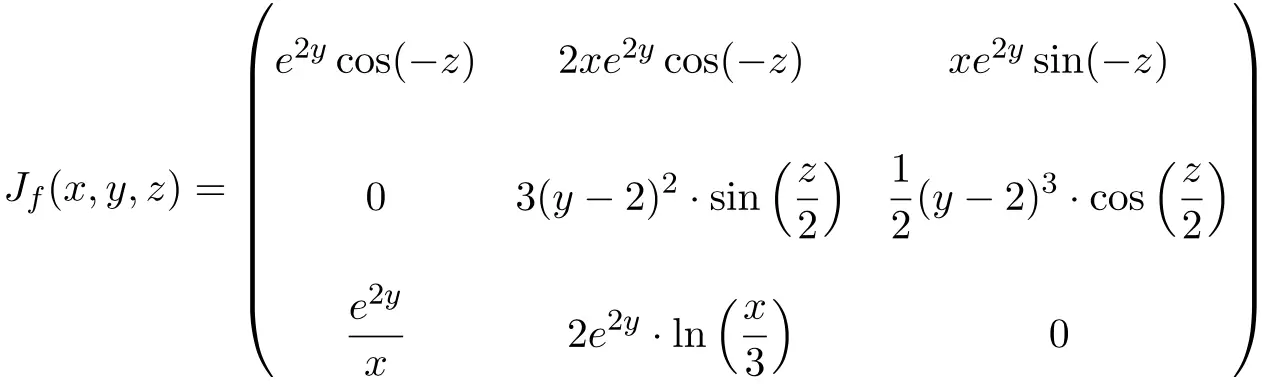
Решение упражнения с матрицей Якобиана 3x3 с 3 переменными

Найдя матрицу Якобиана, мы оцениваем ее в точке

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

Рассчитаем операции:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

И результат матрицы Якоби в этой точке:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Определитель матрицы Якобиана: якобиан

Определитель матрицы Якобиана называется определителем Якобиана или якобианом. Необходимо учитывать, что якобиан можно вычислить только в том случае, если функция имеет такое же количество переменных, как и скалярные функции, поскольку тогда матрица Якобиана будет иметь такое же количество строк, как и столбцов, и, следовательно, она будет квадратом. матрица. .

пример якобиана

Рассмотрим пример вычисления определителя Якобиана функции с двумя переменными:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

Сначала вычислим матрицу Якоби функции:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

А теперь решаем определитель матрицы 2х2:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

Якобиан и обратимость функции

Теперь, когда вы познакомились с концепцией якобиана, вы, вероятно, подумали… ну какой в этом смысл?

Итак, основное использование якобиана — определить, можно ли обратить функцию. Теорема об обратной функции гласит, что если определитель матрицы Якобиана (якобиан) отличен от 0, это означает, что эта функция обратима.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Следует отметить, что это условие является необходимым, но недостаточным, то есть, если определитель ненулевой, мы можем утверждать, что матрицу можно инвертировать, однако, если определитель равен 0, мы не можем знать, является ли функция имеет обратную или нет.

Например, в приведенном ранее примере того, как найти якобиан функции, определитель дает

$4x^2+4y^2$

. В этом случае мы можем утверждать, что функцию можно обратить всегда, кроме точки (0,0), так как эта точка — единственная, где определитель Якоби равен нулю и, следовательно, мы не знаем, будет ли обратная функция существует в этой точке.

Связь матрицы Якоби с другими операциями

Матрица Якобиана связана с градиентом и матрицей Гессе функции:

Склон

Если функция является скалярной функцией, матрица Якобиана будет матрицей-строкой, которая будет эквивалентна градиенту :

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Матрица Гессе

Матрица Якоби градиента функции равна матрице Гессиана :

$\displaystyle H_f = J(\nabla f)$

Гессиан — очень важная матрица для вывода функций с более чем одной переменной, поскольку она формируется вторыми производными функции. Фактически, можно сказать, что матрица Гессе является непрерывностью матрицы Якобиана. Но это настолько важно, что у нас есть целая страница, которая подробно объясняет это. Так что если вы хотите точно узнать, что это за матрица и почему она такая особенная, вы можете перейти по ссылке.

Применение матрицы Якобиана

Помимо замеченной нами полезности якобиана, который определяет, является ли функция обратимой, матрица Якобиана имеет и другие применения.

Матрица Якобиана используется для расчета критических точек многомерной функции, которые затем классифицируются на максимумы, минимумы или седловые точки с помощью матрицы Гессе. Чтобы найти критические точки, необходимо вычислить матрицу Якоби функции, приравнять ее к 0 и решить полученные уравнения.

$\displaystyle J_f(x)=0$

Кроме того, другое применение матрицы Якобиана находится при интегрировании функций с более чем одной переменной, т. е. в двойных, тройных интегралах и т. д. Поскольку определитель матрицы Якоби допускает замену переменной в кратных интегралах по следующей формуле:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Где T — функция изменения переменных, которая связывает исходные переменные с новыми.

Наконец, матрица Якобиана также используется для линейного приближения любой функции.

$f$

вокруг точки

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Якобиан и матрица якобиана

Что такое матрица Якобиана?

Пример расчета матрицы Якобиана

Решенные проблемы матриц Якобиана

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Определитель матрицы Якобиана: якобиан

пример якобиана

Якобиан и обратимость функции

Связь матрицы Якоби с другими операциями

Склон

Матрица Гессе

Применение матрицы Якобиана

Оставьте комментарий Отменить ответ