На этой странице вы узнаете, что такое показательная функция, а также как представить показательную функцию на графике. Кроме того, вы увидите все его характеристики и несколько примеров, чтобы полностью понять его. Наконец, вы сможете попрактиковаться с упражнениями и задачами, шаг за шагом решаемыми на показательных функциях.
Что такое показательная функция?
Определение показательной функции выглядит следующим образом:
В математике показательные функции — это функции, у которых независимая переменная x находится в показателе степени. Другими словами, они заключаются в следующем:
![]()
Золото
![]()
является положительным действительным числом и отличается от 1.
Примеры показательных функций
Следующие функции являются примерами показательных функций:
![]()
![]()
![]()
![]()
Характеристики показательных функций
Экспоненциальные функции обладают следующими свойствами:
- Область определения показательной функции состоит из действительных чисел, или, другими словами, показательная функция существует для любого значения x .
![]()
- Однако функция принимает только положительные значения, поэтому диапазон экспоненциальной функции состоит из положительных действительных чисел.
![]()
- Любая показательная функция является одновременно непрерывной и инъективной функцией.
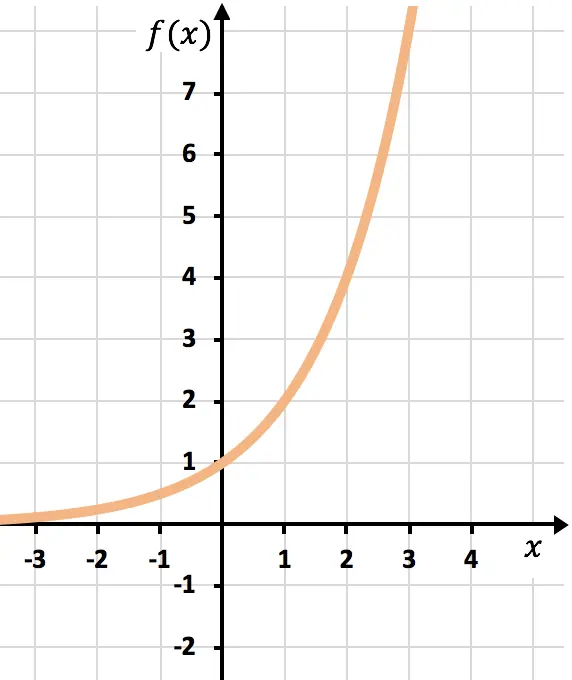
- Если функция не транслируется, любая показательная функция проходит через точку (0,1). Потому что функция, оцененная как ноль, всегда дает единицу.
![]()
- Аналогично, значение показательной функции при x=1 равно основанию.
![]()
- Если энергетическая база
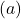
больше 1, показательная функция возрастает. С другой стороны, если коэффициент

находится в интервале между 0 и 1, показательная функция убывает.
- В общем случае ось X представляет собой горизонтальную асимптоту показательной функции.
- Обратная показательная функция – это логарифмическая функция. Следовательно, графики показательной функции и логарифмической функции симметричны относительно прямой y=x, если обе имеют одинаковое основание.
Как построить график экспоненциальной функции
Экспоненциальные функции очень просто представить. Итак, давайте посмотрим, как построить показательную функцию на графике на примере.
- Постройте следующую показательную функцию на графике:
![]()
В показательных функциях нет необходимости вычислять область определения, поскольку все они всегда будут действительными числами:
![]()
Поэтому достаточно составить таблицу значений. Поскольку эти типы функций сильно меняются от одной точки к другой, мы будем рассчитывать 5 точек. Но чем больше точек мы посчитаем, тем точнее будет представление функции.

Для поиска точек в таблице значений рекомендуем воспользоваться калькулятором, так как их сложно посчитать вручную.
Теперь представим точки на графике :

И, наконец, соединяем точки и расширяем функцию:
Обратите внимание, что функция справа продолжает расти до бесконечности.
Напротив, функция слева уменьшается, но никогда не достигает 0. Хотя она и приближается к нему очень близко, она никогда его не касается. Это означает, что линия y=0 (ось X) является горизонтальной асимптотой.
Решенные упражнения на показательные функции
Упражнение 1
Постройте график следующей показательной функции:
![]()
Это показательная функция, поэтому для ее представления необходимо создать таблицу значений, дающую значения переменной x:
![]()
![]()
![]()
![]()
![]()

Получив таблицу значений, мы наносим полученные точки на график и строим функцию:

Обратите внимание, что функция справа продолжает расти до бесконечности. С другой стороны, слева функция убывает, но никогда не превышает 1. Действительно, справа функция имеет горизонтальную асимптоту y=1.
В этом случае горизонтальная асимптота находится в точке y=1 вместо оси OX, поскольку в сторону функции был сделан вертикальный сдвиг на одну единицу вверх.
Упражнение 2
Постройте следующую показательную функцию на графике:
![]()
Это показательная функция, поэтому для ее графического представления необходимо построить таблицу значений, задающих значения переменной x:
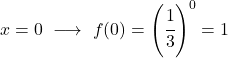
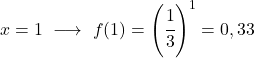
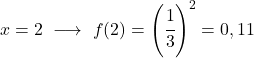
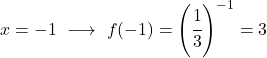
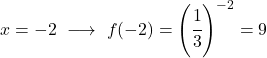
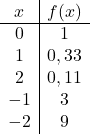
Получив таблицу значений, наносим рассчитанные точки на график и рисуем функцию:

Обратите внимание, что функция слева продолжает расти до бесконечности. С другой стороны, справа функция убывает, но никогда не превышает 0. Действительно, функция имеет горизонтальную асимптоту при y=0 (ось X).
Упражнение 3
Постройте следующую показательную функцию на графике:
![]()
Это показательная функция, поэтому для ее рисования необходимо создать таблицу значений, оценивающую функцию в нескольких точках:
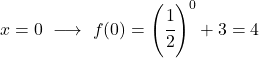
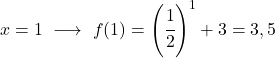
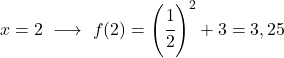
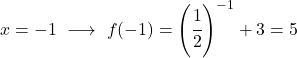
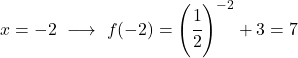

Наконец, представим полученные точки на графике и построим функцию:

Обратите внимание, что функция слева неограниченно возрастает до бесконечности. С другой стороны, справа функция убывает, но никогда не превышает 3. Действительно, функция имеет горизонтальную асимптоту при y=3.
В этом случае горизонтальная асимптота находится на уровне y=3 вместо оси X, поскольку функция была перемещена по вертикали на три единицы вверх.
Упражнение 4
Решите следующую задачу, касающуюся показательных функций.
- Определить стоимость

так что следующая показательная функция проходит через точку (2.8).
![]()
Функция должна проходить через точку (2,8), поэтому мы можем подставить значения x и f(x) точки в функцию, чтобы найти значение константы k:
![]()
И теперь решаем полученное уравнение:
![]()
![]()
![]()
![]()
Упражнение 5
Решите следующую задачу, касающуюся показательных функций.
Популяция термитов размножается по следующей функции:
![]()
Золото
![]()
количество термитов и
![]()
время прошло в месяцах.
Сколько термитов будет через 1 год?
Чтобы подсчитать количество термитов через год, просто подставьте в функцию прошедшее время (1 год). Но поскольку функция t — это количество прошедших месяцев, а не лет, мы должны положить t = 12, поскольку в году 12 месяцев:
![]()
![]()
![]()
Решаем с помощью калькулятора:
![]()
Значит, через год будет 1 594 323 термита.