Что такое векторы (математика)? -Маторство

На этой странице вы найдете все о векторах: что это такое, их характеристики, как они рассчитываются, как выполнять операции с векторами, какие существуют различные типы…

Что такое вектор?

Математическое определение вектора следующее:

В математике вектор — это направленный отрезок, идущий от одной точки (называемой началом координат) к другой точке (называемой концом).

Например, на графике ниже вы можете видеть, что вектор

$\vv{AB}$

Он имеет точку А в качестве начала и точку В в качестве конечной точки.

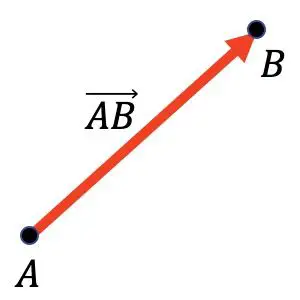
Векторы в основном используются в математике, особенно в геометрии и физике, для графического представления векторных сил.

Характеристики вектора

Раз мы поняли, в чем заключается математический смысл векторов, давайте теперь посмотрим, каковы их свойства.

Каждый вектор имеет следующие геометрические характеристики:

Направление : направление вектора — это направление линии, содержащей вектор, или любой линии, параллельной ему. Другими словами, направление вектора — это линия, на которой он лежит.
Направление : направление вектора — это ориентация указанного вектора, указанная его стрелкой.
Модуль (или величина): модуль вектора — это его длина, соответствующий числовому значению вектора. Следовательно, чем больше означает вектор, тем большую векторную величину он представляет.
Точка приложения : точкой приложения вектора является начало координат указанного вектора.

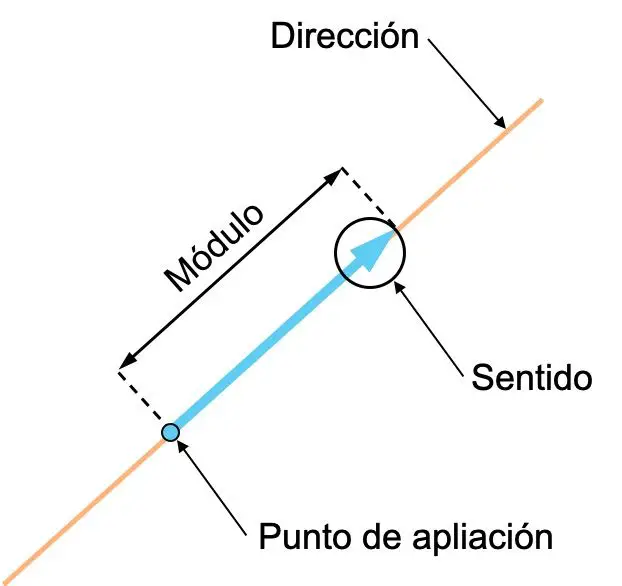
Понятия направления и направления вектора часто сбивают с толку, поэтому важно различать между ними разницу. Посмотрите на следующий пример с двумя векторами, оба имеют одинаковое направление, но имеют разное значение:

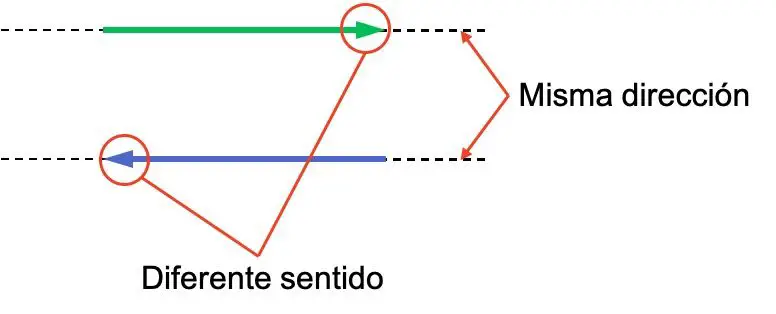
Оба вектора имеют одинаковое направление, поскольку они параллельны. Вместо этого их направления противоположны, потому что они обращены назад.

Компоненты вектора

Мы только что видели, что векторы графически изображаются стрелками, но векторы также могут быть представлены численно компонентами (или координатами) вектора.

Например, если у нас есть следующий вектор, представленный на графике:

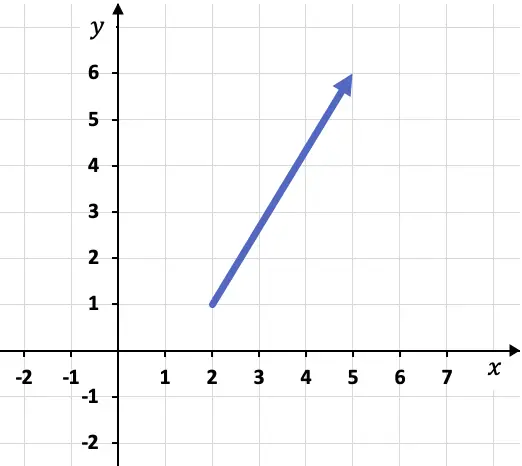
Чтобы вычислить компоненты вектора, нам необходимо сначала определить координаты его начала и конца, то есть точки, где он начинается и где заканчивается. В этом случае начало и конец вектора:

Происхождение вектора: A(2,1)

Конечная точка вектора: B(5,6)

Итак, чтобы найти координаты или компоненты вектора, просто вычтите конечную точку минус начало координат:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

Итак, компоненты вектора, представленного на графике, таковы:

$\vv{\bm{AB}}\bm{=(3,5)}$

Векторные операции

добавление вектора

Чтобы численно сложить два вектора, необходимо сложить их соответствующие компоненты. Другими словами, координаты X двух векторов складываются и совпадают с координатами Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Чтобы вы могли увидеть, как это делается, мы добавим следующие два вектора:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

Два вектора также можно добавить из их графических представлений. Для этого обычно используют правило или закон параллелограмма, но существует множество методов. Здесь вы можете увидеть примеры и решенные упражнения о том , как графически сложить два вектора .

векторное вычитание

Чтобы аналитически вычесть два вектора, необходимо вычесть их соответствующие компоненты. То есть координаты X двух векторов вычитаются друг из друга и совпадают с координатами Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

В качестве примера мы вычтем следующие два вектора:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Подобно сложению, вы также можете вычесть 2 вектора, используя их представления. Для этого обычно используют правило или закон треугольника, но существует несколько методов. Вы можете увидеть их все на примерах и решенных упражнениях на вычитание двух векторов графически .

модуль вектора

Как мы видели в начале этой страницы, величина вектора соответствует длине этого вектора. Что ж, длину (или величину) вектора можно определить по его компонентам.

Рассмотрим любой вектор:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Чтобы найти величину вектора на плоскости, необходимо применить следующую формулу:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Например, мы рассчитаем величину следующего вектора по формуле:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Хотя это кажется очень простым, определение величины вектора может оказаться сложной задачей. Если вы хотите увидеть больше примеров и попрактиковаться в решенных упражнениях модуля вектор , мы рекомендуем вам посетить эту связанную страницу.

Умножение вектора на скаляр

Чтобы численно вычислить произведение вектора на число (или скаляр), каждый компонент вектора необходимо умножить на это число.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

В следующем общем примере вы можете увидеть, как направление вектора сохраняется независимо от знака скаляра. С другой стороны, направление вектора зависит от знака числа, которое он умножает.

умножение или произведение числа или скаляра на вектор

Ниже вы можете увидеть численный пример того, как найти произведение вектора и числа:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Скалярное произведение

В аналитической геометрии скалярное произведение — это векторная операция, которая умножает два вектора и преобразует их в действительное число.

Таким образом, формула скалярного произведения двух векторов выглядит следующим образом:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Ниже приведен пример расчета результата скалярного произведения двух векторов:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

По этой ссылке вы можете увидеть больше примеров скалярного произведения . Кроме того, вы найдете еще один способ нахождения скалярного произведения между двумя векторами, свойства этого типа операций с векторами и упражнения, решаемые шаг за шагом.

векторный продукт

Хотя они очень похожи по названию, скалярное произведение и векторное произведение совершенно разные.

Перекрестное произведение , также называемое перекрестным произведением, — это операция между двумя векторами в пространстве (в R3), то есть они являются трехкоординатными векторами.

Итак, если у нас есть любые два трёхмерных вектора:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Перекрестное произведение двух векторов равно результату следующего определителя 3×3:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

где векторы

$\vv{i}, \vv{j},\vv{k}$

— единичные векторы в направлениях осей X, Y, Z соответственно.

Кроме того, направление результирующего вектора перпендикулярно двум перемноженным векторам.

Как вы можете догадаться, решение этого типа операций сложнее предыдущих, и по этой причине у нас есть целая страница с подробным объяснением того, как вычисляется векторное произведение между двумя векторами. Поэтому, если вам интересно, рекомендуем посетить его и попрактиковаться с решенными упражнениями на векторное произведение .

смешанный продукт

Смешанное произведение трех векторов, также называемое тройным скалярным произведением, представляет собой последовательное умножение трех векторов, включающее два разных типа операций: скалярное произведение и векторное произведение. Итак, комбинация двух векторных операций дает скаляр (действительное число).

Конкретно смешанное произведение состоит из вычисления векторного произведения двух векторов и последующего векторного умножения полученного результата на третий вектор. Посмотрите на формулу:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Как и в случае с векторным произведением, решение смешанного произведения векторов непросто. По этой причине мы рекомендуем вам взглянуть на это объяснение смешанного произведения трех векторов , где вы найдете примеры, решенные упражнения и геометрический смысл этой векторной операции.

типы векторов

Существует много различных типов векторов, но наиболее важными определениями, которые следует знать, являются:

Единичный вектор : вектор, модуль которого равен 1.
Фиксированный вектор : вектор фиксируется, когда начало вектора применяется к фиксированной точке.
Свободный вектор : вектор свободен, если его точка приложения не определена, но является свободной точкой.
Коллинеарные векторы : два или более вектора являются коллинеарными, если они имеют одну и ту же линию действия (линию, на которой расположен вектор).
Эквивалентные векторы : два вектора являются равнопыльными, если они имеют одинаковый размер, одинаковый смысл и одинаковое направление (хотя они могут иметь разные точки приложения).
Связанные векторы : Связанные векторы — это равнопыльцевые векторы, которые также действуют на одной линии.
Противоположные векторы : два вектора противоположны, если они имеют одинаковую величину и одинаковое направление, но разное направление.
Вектор положения : вектор положения — это вектор, начало координат которого является точкой (0,0) (начало координат).
Конкурирующие векторы : два или более вектора совпадают, когда их линии действия проходят через одну и ту же точку, то есть они пересекаются.
Параллельные векторы : два или более вектора параллельны, если они имеют одинаковое направление, независимо от их направления.
Перпендикулярные векторы : два вектора перпендикулярны (или ортогональны), если их направления образуют угол 90°.
Ортонормированные векторы : Два или более вектора являются ортонормированными, если они перпендикулярны друг другу и, более того, унитарны (их величина равна единице).
Копланарные векторы : два или более вектора являются копланарными, если они лежат в одной плоскости.

Угол между двумя векторами

Чтобы найти угол между двумя заданными векторами, мы должны применить следующую формулу:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Золото

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

являются модулями векторов

$\vv{\text{u}}$

$\vv{\text{v}}$

соответственно.