Число Пи — это математическая константа , которая представляет собой соотношение между длиной окружности и ее диаметром. Это иррациональное число. Другими словами, это не точная дробь . Следовательно, его нельзя представить в виде конечного десятичного числа. Значение Пи составляет примерно 3,14159 и обозначается греческой буквой π.
Пи – важное число в математике. Поэтому он имеет множество применений в различных областях. Например, он используется в геометрии для вычисления площади. А также периметр кругов и других круглых фигур. С другой стороны, в тригонометрии вычисляются углы и длины дуг. Наконец, в технике и физике для расчета таких величин, как объем и емкость.
День Пи отмечается ежегодно 14 марта, поскольку эта дата близка к значению числа Пи (3,14). Эта дата отмечается в ознаменование роли Пи в математике и повышения интереса к этой фундаментальной константе.
Кто открыл число Пи?
Число Пи известно с античных времен, и именно греческий математик Архимед (287-212 до н.э.) описал его точно. Фактически, он использовал его для расчета площади и объема геометрических фигур.
В 18 веке швейцарский математик Иоганн Ламберт доказал, что Пи — иррациональное число . Позже, в XIX веке, немецкий математик Фердинанд фон Линдеманн объяснил, что Пи — трансцендентное число . То есть его нельзя выразить как точное решение полиномиального уравнения с рациональными коэффициентами.
На протяжении всей истории разные математики вносили свой вклад в понимание числа Пи и разрабатывали методы его более точного вычисления. Сегодня Пи остается одной из самых важных и самых известных математических констант в мире и продолжает оставаться предметом изучения математики.
Почему число Пи бесконечно?
Значение Пи составляет приблизительно 3,14159, но на самом деле это число, которое продолжается бесконечно после десятичной точки. Это означает, что Пи — бесконечное число и не может быть полностью представлено десятичным числом.
Хотя значение Пи бесконечно, на практике приближенные значения Пи можно рассчитать с большой точностью. К настоящему времени были вычислены миллионы цифр числа Пи и было показано, что десятичные цифры не имеют регулярной закономерности. Хотя это было сделано с помощью суперкомпьютеров, потому что мы не можем вычислить столько чисел.
Какие существуют методы расчета приблизительного значения числа Пи?
Существует несколько практических методов расчета значения числа Пи.Далее мы шаг за шагом объясним три метода, наиболее часто используемые математиками.
1. Метод Архимеда
Греческий математик Архимед использовал геометрический метод для расчета приблизительного значения числа Пи. Чтобы использовать этот метод, выполните следующие действия:
1. Нарисуйте круг, проведите линию через центр круга и пересечите ее в двух противоположных точках, как показано ниже:
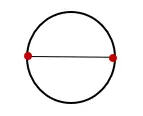
2. Измерьте длину линии, пересекающей круг, и назовите ее буквой «D». Это измерение и есть диаметр круга.
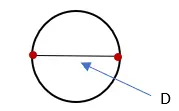
3. Измерьте длину линии, образующей круг, и назовите ее буквой «C». Это измерение является окружностью круга.
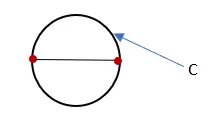
4. Разделите длину окружности (C) на диаметр круга (D). Результатом является приблизительное значение Пи.
Например: если диаметр круга равен 6, а длина окружности равна 18, то приблизительное значение Пи составляет 18 ÷ 6 = 3. Очевидно, что этот пример очень простой, но если вы сделаете это со значениями фактической длины окружности . , вы увидите, что метод работает правильно.
На самом деле, мы рекомендуем попробовать: измерить чашку или что-то круглой формы и посмотреть, подойдет ли это вам.
2. Метод Монте-Карло
Метод Монте-Карло — вероятностный метод, используемый для расчета приближенных значений числа Пи.Для этого на плоскости случайным образом генерируется большое количество точек и подсчитывается количество точек, попадающих в круг, вписанный в квадрат. Процесс применяется следующим образом:
1. Нарисуйте круг внутри квадрата со стороной 1, как показано ниже:

2. Случайным образом сгенерируйте большое количество точек в квадрате.
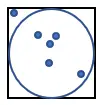
3. Подсчитайте количество точек, попавших в круг. Назовем эту величину «n».
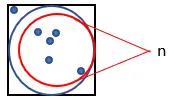
4. Подсчитайте общее количество набранных баллов. Назовите эту величину «м».
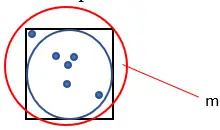
5. Рассчитайте приблизительное значение Пи по следующей формуле: Пи = (4 · n) ÷ m.
Например, если было сгенерировано 380 точек и 300 поместилось в круг, то приблизительное значение Пи составит (4 · 300) ÷ 380 = 3,16. Это значение очень похоже на первые два знака после запятой числа Пи, но, как и в предыдущем методе, использование фактических измерений даст вам еще более точное значение .
3. Итерационный метод
Итерационный метод — это математический метод, используемый для расчета приближенных значений числа Пи. Этот метод использует формулу, подразумевающую значение числа Пи, и применяется итеративно для повышения точности расчета. Вот шаги по использованию этого метода:
- Выберите начальное значение числа Пи. Например, вы можете выбрать значение 3.
- Используйте формулу, включающую значение числа Пи, чтобы вычислить новое приблизительное значение. Например, вы можете использовать следующую формулу: Пи = (Пи + (4 ÷ Пи)) ÷ 2.
- Сравните новое приблизительное значение со старым значением. Если разница между ними достаточно мала, вы получили точный результат. Если разница все еще значительна, присвойте новое значение Pi и повторите процесс, начиная с шага 2.
Например, если начальное значение Pi равно 3, новое приблизительное значение будет (3 + (4 ÷ 3)) ÷ 2 = 2,66666666. Но поскольку разница между ними не очень мала , вы всегда можете повторить процесс несколько раз, прежде чем найти точное значение.
Каково применение числа Пи?
Пи — важное число в математике и имеет множество приложений в различных областях. Среди наиболее важных применений Пи можно отметить следующие:
Геометрия
Пи используется в геометрии для расчета площади и периметра кругов и других круглых фигур:
- Круги : вычислите площадь и периметр кругов.
- Сферы : определите площадь и объем сфер.
- Цилиндры : Расчет площади поверхности и объема цилиндров.
- Конусы – используется для расчета площади поверхности и объема конусов.
Тригонометрия
Это полезно в тригонометрии для расчета углов и длин дуг. Некоторые из его применений:
- Углы : расчет углов и длин дуг.
- Тригонометрические функции – используются для расчета значения тригонометрических функций для определенных углов.
- Круговая тригонометрия : для расчета значений тригонометрических функций для углов 360 градусов.
Инженерное дело
В технике Пи используется для расчета таких величин, как объем и емкость. Некоторые из его применений:
- Электроника : расчет таких величин, как сопротивление и емкость.
- Электричество : используется для расчета таких величин, как мощность и электрическая энергия.
- Гражданское строительство : расчет таких величин, как площадь поверхности и объем конструкций и строительных элементов.
Физический
Число Пи (π) — математическая константа, имеющая множество приложений в физике. Вот несколько примеров использования числа Пи в физике:
- Волны – используется для расчета частоты и длины волн.
- Механика : В механике полезен для расчета работы и энергии во вращающихся системах.
- Электромагнетизм . В электромагнетизме его можно использовать для расчета энергии, запасенной в конденсаторе, и индуктивности обмотки.
- Космология В космологии число Пи используется для расчета кривизны пространства-времени и расширения Вселенной.
Какое применение имеет число Пи в реальной жизни?
Вот несколько примеров того, как число Пи используется в повседневной жизни:
- Геометрия : определить площадь круглого коврика или измерить длину рулетки, необходимую для покрытия периметра круглого стола.
- Приготовление пищи — определение того, сколько воды или жидкости необходимо для заполнения кастрюли или сколько ингредиентов поместится в круглый контейнер.
- Астрономия : знать расстояние между планетами и звездами, орбиты планет и положение небесных тел на небе.
- Садоводство : узнайте количество почвы или почвы, необходимое для заполнения круглого горшка, или рассчитайте количество воды, необходимое для полива растения в круглом саду.