Здесь вы найдете объяснение, что это такое и как называются все части многочлена (степень, переменные, независимый член и т. д.). Кроме того, вы сможете увидеть несколько примеров и попрактиковаться в частях многочлена с помощью решенных упражнений.
Но прежде чем увидеть, что представляют собой все части многочлена, давайте быстро рассмотрим его математическое определение, чтобы полностью понять концепцию: многочлен — это алгебраическое выражение, образованное сложением или вычитанием мономов разных степеней.
Каковы части многочлена?
Частями многочлена являются:
- Члены : каждая мономиальная часть многочлена.
- Коэффициенты : числа, сопровождающие каждый член многочлена.
- Степень : наибольший показатель степени, до которого возводится полиномиальная переменная.
- Переменная : буква, которую имеет полином.
- Главный член : член высшей степени полинома.
- Независимый член : член многочлена, который не содержит переменной.
- Доминантный коэффициент : коэффициент доминантного члена полинома.
Когда многочлен имеет только одну переменную, его степень равна наибольшему показателю степени его членов. Однако если многочлен имеет две или более переменных, узнать его степень сложнее, поскольку необходимо выполнить операцию. Узнайте, как это сделать, нажав на следующую ссылку степени полинома двух (или более) переменных .
Как определить части многочлена
Части или элементы многочлена можно легко найти визуально. Посмотрите, как это делается, на следующей схеме:
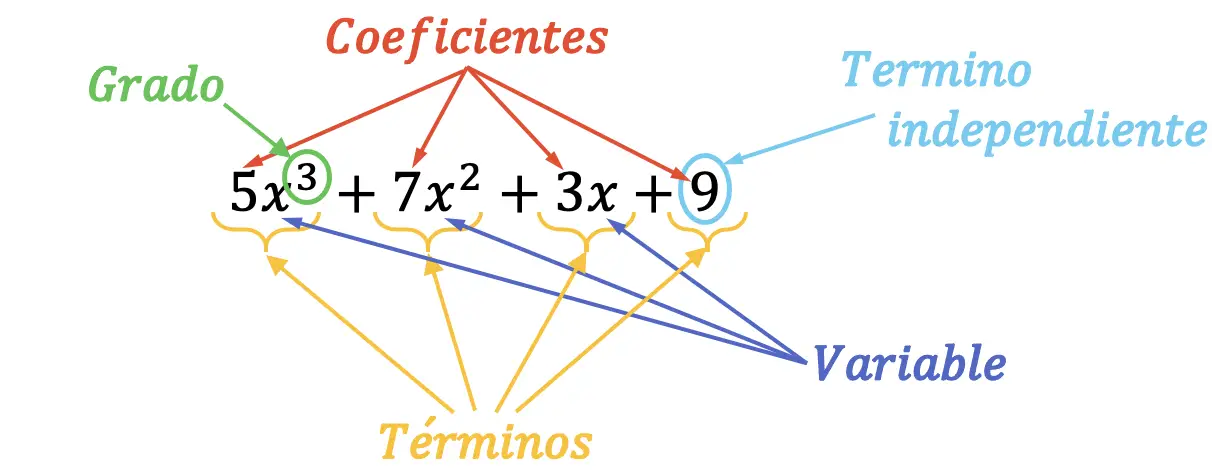
У предыдущего многочлена третьей степени отмечены все его части. Кроме того, главный член указанного многочлена равен примерно 5×3 , поскольку это моном высшей степени. Аналогично, старший коэффициент многочлена равен 5, поскольку это коэффициент ведущего члена.
В этом случае полином имеет одну переменную и, следовательно, имеет только один тип степени. Но вы должны знать, что когда полином является многомерным, вам необходимо различать абсолютную степень и относительную степень переменной. Из чего состоит каждый из них вы можете посмотреть по ссылке, которую я вам оставил выше ⬆⬆ ( степень многочлена двух переменных ).
Примеры частей многочлена
Чтобы закончить понимание значения частей многочлена и выполняемой ими функции, мы увидим несколько примеров определения частей любого типа многочлена:
Пример 1
Определите части следующего квадратичного многочлена (степени 2):
![]()
- Условия: 4x 2 , -8x, 1
- Коэффициенты: 4, -8, 1
- 2-й год
- Переменная: х
- Основной термин: 4x 2
- Независимый мандат: 1
- Коэффициент рулевого управления: 4
С другой стороны, следует отметить, что многочлен в этом примере называется трехчленом . Что представляет собой этот тип полинома, вы можете увидеть на примерах трёхчленов . Кроме того, вас также может заинтересовать другой тип полинома, называемый биномиальным (с ним проще производить некоторые операции), в чем его особенность, вы можете увидеть на биномиальных примерах .
Пример 2
Найдите части следующего многочлена:
![]()
- Условия: y 3 , 9y 2 , -5y, 3
- Коэффициенты: 1, 9, -5, 3
- 3-й год
- переменные: и
- Основной термин: и 3
- Независимый мандат: 3
- Коэффициент рулевого управления: 1
Как вы можете видеть в этом примере, если перед мономом нет числа, это означает, что его коэффициент равен единице. Значит, старший коэффициент этого многочлена равен 1.
Решенные упражнения с частями многочлена
Чтобы помочь вам запомнить названия всех частей многочлена, мы подготовили для вас несколько решаемых упражнений. Все интересующие вас вопросы по ним вы можете задать нам в комментариях. ⬇⬇
Упражнение 1
Найдите все части следующего многочлена:
![]()
Полином в этом упражнении не имеет независимого члена, поскольку все члены состоят как минимум из одной переменной (или буквы).
Условия: 2х4 , 6х2 , х
Коэффициенты: 2, 6, 1
Уровень 4
Переменная: х
Основной термин: 2×4
Самостоятельный термин: нет
Коэффициент рулевого управления: 2
Упражнение 2
Найдите все части следующего многочлена:
![]()
Полином в этой задаче состоит из двух переменных: x и y. Еще:
Условия: -7x 4 y 2 , 3x 4 , -5y 2 , xy, -10.
Коэффициенты: -7, 3, -5, 1, -10
6-й курс
Переменные: x, y
Основной член: -7x 4 и 2
Независимый мандат: -10
Коэффициент рулевого управления: -7
Как видите, для решения подобных многочленов вам нужно знать, как вычислить степень многочлена с более чем одной переменной. Если вы все еще не знаете, как это сделать, я рекомендую перейти по ссылке выше в разделе «Каковы части многочлена?». ( степень многочлена двух переменных ). ⬆⬆ Вы найдете пошаговое объяснение, а также несколько примеров.
Хотя это радикально другая концепция, если вы зашли так далеко, вам наверняка будет интересно узнать, что такое полиномиальное выражение числа. Это то, о чем мало кто знает, но на самом деле это очень полезно.