Функция прямой пропорциональности

В этой статье мы объясним, что такое функции прямой пропорциональности, какова их формула, как представить их на графике и как вычислить их уравнение из заданной точки.

Что такое функция прямой пропорциональности?

Функция прямой пропорциональности – это функция, связывающая две прямо пропорциональные величины. Следовательно, чтобы вычислить значение зависимой переменной (y), значение зависимой переменной (x) необходимо умножить на константу пропорциональности.

Функцию прямой пропорциональности еще называют линейной функцией.

Помните, что две величины прямо пропорциональны, если стоимость одной величины увеличивается, а стоимость другой также увеличивается, и наоборот.

Формула функции прямой пропорциональности

Формула, определяющая функцию прямой пропорциональности, выглядит следующим образом:

$y=mx$

где y — независимая переменная, x — зависимая переменная, а ym — наклон или константа пропорциональности функции.

Как видите, по этой формуле очень легко вычислить значения величины у, достаточно умножить значение величины х на наклон функции, характерный для каждой функции прямой пропорциональности.

Например, если у нас есть следующая функция прямой пропорциональности:

$y=3x$

Если мы хотим определить, какова величина y, когда x равен 5, нам нужно всего лишь умножить наклон функции (3) на 5:

$y=3\cdot 5=15$

Графическое представление функции прямой пропорциональности

Далее мы увидим, как построить график функции прямой пропорциональности. В качестве примера мы выполним следующее упражнение:

$y=2x$

Чтобы представить функцию прямой пропорциональности на графике, просто проведите линию, проходящую через начало координат (точку (0,0)) и имеющую наклон функции.

В этом случае функция, которую мы хотим представить, имеет наклон

$m=2$

Следовательно, линия должна вырасти на две единицы y на каждую единицу x.

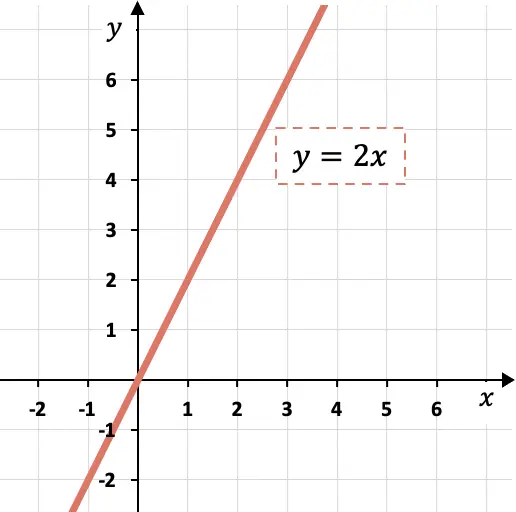
Как видно из графика, если наклон равен 2, это означает, что величина y увеличивается в два раза больше, чем величина x.

Функции прямой пропорциональности имеют очень похожий график на аффинные функции, но это два разных типа функций. Вы можете увидеть, в чем разница между аффинной функцией и линейной функцией, по следующей ссылке:

➤ См.: разница между линейной и аффинной функцией.

Как найти функцию прямой пропорциональности

Зная точку функции прямой пропорциональности, мы легко находим ее уравнение. Давайте посмотрим, как это делается, решив задачу о прямой пропорциональности:

Количество комнат, которые рисует маляр, примерно прямо пропорционально количеству часов, которые он работает, то есть чем больше часов он работает, тем больше комнат он может нарисовать. Если мы знаем, что за 8-часовой день он покрасил целых две комнаты, какова функция прямой пропорциональности, связывающая количество покрашенных комнат с отработанным временем?

Во-первых, нам нужно определить, какая переменная является зависимой, а какая независимой. Количество нарисованных деталей зависит от отработанного времени, а не наоборот. Следовательно, независимая переменная (x) — это количество отработанных часов, а зависимая переменная (y) — количество покрашенных комнат.

Задача подсказывает нам, что маляр может покрасить 2 комнаты за 8 часов, поэтому график функции должен проходить через точку (8,2).

$(8,2)$

Кроме того, в заявлении указывается, что эти две величины имеют прямо пропорциональную связь, а это означает, что они математически связаны с формулой функции прямой пропорциональности:

$y=mx$

Теперь мы можем вычислить значение наклона функции, подставив координаты точки (8,2) в уравнение:

$y=mx \ \xrightarrow{x=8 \ ; \ y=2}\ 2=m\cdot 8$