▷ Вогнутость и выпуклость функции (кривизна)

Здесь вы узнаете, что такое вогнутость и выпуклость функции и как определить, является ли функция вогнутой или выпуклой. Кроме того, вы сможете попрактиковаться с помощью пошаговых упражнений на кривизну функции.

Что такое вогнутость и выпуклость функции?

Вогнутость и выпуклость функции относятся к кривизне графика функции. Вогнутая функция — это функция, график которой имеет форму горы, а выпуклая функция — это функция, график которой имеет форму долины.

В предыдущем абзаце вогнутая и выпуклая функции были определены неформально для простоты понимания, но математическое определение вогнутой и выпуклой функций выглядит следующим образом:

Вогнутая функция: когда отрезок, соединяющий любые две точки функции, находится ниже кривой.
Выпуклая функция: когда отрезок, соединяющий любые две точки функции, находится над кривой.

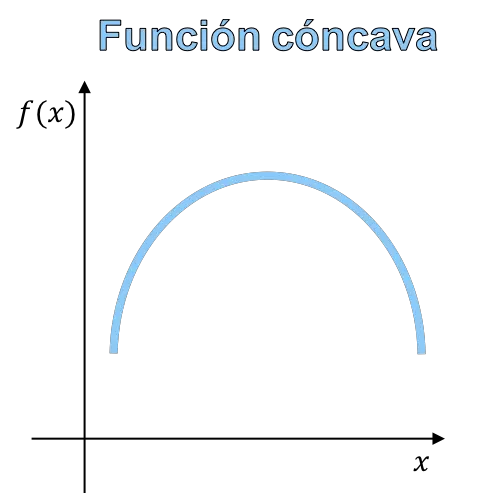
В конечном счете, разница между вогнутой функцией и выпуклой функцией заключается в форме функции, и, следовательно, вы можете отличить вогнутость от выпуклости по графику функции.

Однако функция не обязательно должна быть вогнутой или выпуклой во всей своей области определения, но также может быть вогнутой в одном интервале и выпуклой в другом интервале.

Примечание. Математическое сообщество до сих пор не до конца с этим согласны и поэтому некоторые профессора говорят обратное: они называют вогнутой функцию, имеющую форму

$\bm{\cup}$

и выпуклая функция, имеющая вид

$\bm{\cap}$

. В любом случае важно знать, что это за функция, как бы она ни называлась.

Как изучить кривизну функции

Изучение кривизны функции предполагает нахождение вогнутости и выпуклости функции, то есть знание интервалов, в которых функция вогнута, и интервалов, в которых функция выпукла.

Итак, для изучения кривизны функции необходимо выполнить следующие действия:

Найдите точки, не принадлежащие области определения функции.
Вычислите первую производную и вторую производную функции.
Найдите корни второй производной , то есть вычислите точки, которые сокращают вторую производную, решив
$f''(x)=0$

.
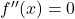
Сделайте интервалы между корнями производной и точками, не принадлежащими области определения функции.
Вычислите значение второй производной в точке каждого интервала.
Таким образом, знак второй производной определяет вогнутость или выпуклость функции на этом интервале:
- Если вторая производная функции положительна, то функция выпуклая на этом интервале.
- Если вторая производная функции отрицательна, функция на этом интервале вогнутая .

Пример того, как найти кривизну функции

Далее мы шаг за шагом решим пример, чтобы вы могли увидеть, как вычисляются интервалы вогнутости и выпуклости функции.

Изучите вогнутость и выпуклость следующей функции:

$f(x)=x^3-3x$

Первое, что нужно сделать, это вычислить область определения функции. В данном случае мы имеем полиномиальную функцию, поэтому область определения функции состоит из действительных чисел:

$\text{Dom } f= \mathbb{R}$

После того, как мы вычислили область определения функции, нам нужно выяснить, в каких точках вторая производная функции обращается в нуль.

Поэтому мы вычисляем первую производную функции:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

Затем находим вторую производную функции:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

А теперь приравняем вторую производную к 0 и решим уравнение:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

После того, как мы вычислили область определения функции и

$f''(x)=0$

, мы представляем все критические точки, найденные на прямой. В данном случае мы не нашли критической точки при расчете области определения функции, но получили точку, сокращающую вторую производную функции:

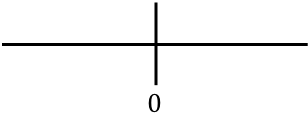
А теперь мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Поэтому мы берем точку в каждом интервале (никогда не критические точки) и смотрим, какой знак имеет вторая производная в этой точке:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Наконец, выведем интервалы вогнутости и выпуклости функции. Если вторая производная положительна, это означает, что функция выпуклая.

$(\bm{\cup})$

, и если вторая производная отрицательна, это означает, что функция вогнутая

$(\bm{\cap})$

. Таким образом, интервалы вогнутости и выпуклости функции равны:

Выпуклый

$(\bm{\cup})$

$\bm{(0,+\infty)}$

Вогнутый

$(\bm{\cap})$

$\bm{(-\infty,0)}$

Решенные упражнения на вогнутость и выпуклость функции

Упражнение 1

Вычислите интервалы вогнутости и выпуклости следующей полиномиальной функции:

$f(x) = x^3-3x^2-2x$

Посмотреть решение

Функция в упражнении является полиномом, поэтому область определения функции состоит из действительных чисел:

$\text{Dom } f= \mathbb{R}$

Определив область определения функции, продифференцируем ее:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

Затем находим вторую производную функции:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

А теперь приравняем вторую производную к 0 и решим уравнение:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

После того, как мы вычислили область определения функции и решили

$f''(x)=0$

, представим все особые точки, найденные на числовой прямой:

А теперь возьмем точку, принадлежащую каждому интервалу, и посмотрим, какой знак имеет вторая производная в этой точке:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

Когда вторая производная больше нуля, это означает, что функция выпуклая.

$(\bm{\cup})$

, но когда вторая производная отрицательна, это означает, что функция вогнутая

$(\bm{\cap})$

. Следовательно, интервалы вогнутости и выпуклости равны:

Выпуклый

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Вогнутый

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Упражнение 2

Изучите кривизну следующей рациональной функции:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Посмотреть решение

Сначала нам нужно вычислить область определения функции. Поскольку это рациональная функция, мы приравниваем знаменатель к нулю, чтобы увидеть, какие числа не принадлежат области определения функции:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Это означает, что когда x равен -2 или +2, знаменатель будет равен 0. И, следовательно, функция не будет существовать. Таким образом, область определения функции состоит из всех чисел, кроме x=-2 и x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Во-вторых, вычисляем первую производную функции:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

И затем решаем вторую производную:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Все члены умножаются на

$(x^2-4)$

. Таким образом, мы можем упростить дробь:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Теперь вычислим корни второй производной функции:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Термин

$\left(x^2-4\right)^3$

Это предполагает деление всей левой части, чтобы мы могли умножить ее на всю правую часть:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Выделим общий множитель:

$x(8x^2+96)=0$

Чтобы умножение было равно 0, один из двух элементов умножения должен быть нулем. Поэтому мы устанавливаем каждый фактор равным 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Решения нет, поскольку из действительного числа нет отрицательного корня.

Теперь мы представим на прямой все полученные критические точки, то есть точки, которые не принадлежат области определения (x=-2 и x=+2) и те, которые сокращают вторую производную (x=0):

И мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Итак, мы берем точку в каждом интервале и смотрим, какой знак имеет вторая производная в этой точке:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Если вторая производная положительна, это означает, что функция выпуклая.

$(\bm{\cup})$

, и если вторая производная отрицательна, это означает, что функция вогнутая

$(\bm{\cap})$

. Следовательно, интервалы вогнутости и выпуклости равны:

Выпуклый

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Вогнутый

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Упражнение 3

Функция

$f(x)$

имеет относительную крайность в

$x=3$

. Более того, функция выпуклая

$(\cup )$

в этот же момент. Определите, является ли относительный экстремум минимумом или максимумом.

➤ См.: определение максимумов и минимумов функции.

Посмотреть решение

Пусть выпуклая функция

$(\cup)$

$x=3$

означает, что вторая производная в этой точке положительна, т.е.

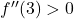$f''(3)>0″ title=»Rendered by QuickLaTeX.com» height=»19″ width=»74″ style=»vertical-align: -5px;»></p> <p> .</p> <p class=$ Таким образом, относительный крайний

$\bm{x=3}$

Это минимум , так как

$f''(3)$

Это позитивно.

Что такое вогнутость и выпуклость функции?

Как изучить кривизну функции

Пример того, как найти кривизну функции

Решенные упражнения на вогнутость и выпуклость функции

Упражнение 1

Упражнение 2

Упражнение 3

Оставьте комментарий Отменить ответ