Как факторизовать полиномы (полиномиальный факторинг)

На этой странице мы объясняем, как факторизовать полином любого типа. Сначала мы увидим, как факторизовать многочлен с помощью правила Руффини, затем перейдем к тому, как факторизуются многочлены без независимого члена, затем мы проанализируем факторизацию корневых многочленов с дробями и, наконец, частные случаи факторизации (примечательные тождества, факторизация по группировкам, трехчлены и т. д.). Все пояснения даны на примерах, а в конце вы сможете попрактиковаться с пошагово решенными упражнениями по факторизации многочленов.

Что такое полиномиальная факторизация?

Полиномиальная факторизация — это метод, используемый в математике для разложения многочлена на произведение факторов.

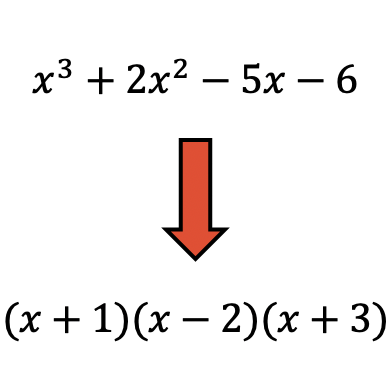
Факторизация полиномов очень полезна, поскольку с факторизованными полиномами легче выполнять операции.

Теперь, когда мы знаем, что такое факторизация полиномов, давайте посмотрим, как факторизуются полиномы.

Как факторизовать многочлены по правилу Руффини

Очевидно, чтобы понять, как факторизовать полином с помощью правила Руффини, вы должны сначала знать , как применять правило Руффини . Поэтому мы оставляем вам эту ссылку на случай, если вы захотите сначала просмотреть, как выглядит процедура.

Чтобы факторизовать многочлен, необходимо выполнить следующие шаги:

1. Корни многочлена вычисляются по правилу Руффини.
2. Каждый найденный корень типа x=a выражается в виде множителя (xa).
3. Факторизованный полином представляет собой произведение всех найденных коэффициентов, умноженное на коэффициент члена высшей степени невзвешенного полинома.

Чтобы вы могли увидеть, как это делается, и лучше понять процедуру факторизации полиномов, ниже вы найдете конкретный пример, объясненный шаг за шагом:

• Фактор следующего полинома:

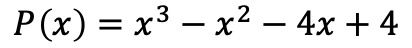
Первое, что нужно сделать, это вычислить корни или нули многочлена. Для этого нам необходимо найти делители независимого члена многочлена , которые в данном случае равны ±1, ±2 и ±4.

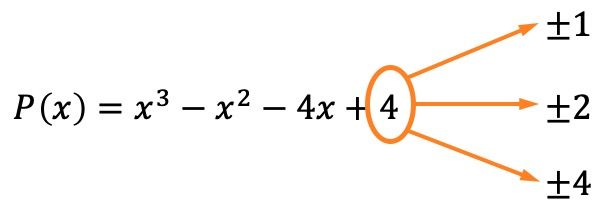
Теперь мы знаем, благодаря теореме об остатках и множителях, что если остаток от деления многочлена на одно из этих значений равен 0, это означает, что указанное значение является корнем многочлена.

Поэтому мы должны разделить многочлен на каждый из делителей независимого члена по правилу Руффини и посмотреть, в каких случаях остаток равен нулю.

Например, мы начнем с применения правила Руффини с

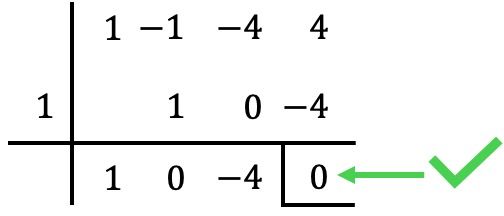
В этом случае остаток (или вычет) от деления равен нулю, поэтому

Это корень многочлена. ✅

Отлично, корень многочлена у нас уже есть, осталось только определить остальные оставшиеся корни. Для этого воспользуемся правилом Руффини с другим делителем независимого члена, например

Кроме того, нет необходимости использовать метод Руффини с целочисленным полиномом, но мы можем продолжить с того места, где остановились на предыдущем шаге:

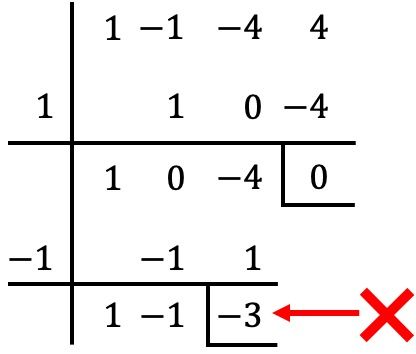
Однако в этом случае при делении на

полученный остаток отличен от 0, поэтому

Это не корень многочлена. ❌

Поэтому мы должны попробовать другое значение, например, мы выполняем правило Руффини с помощью

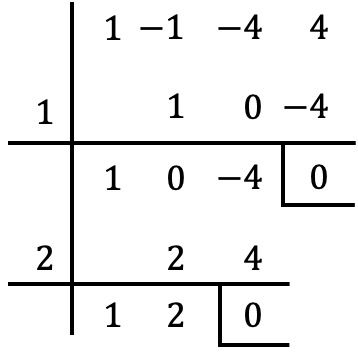
В этом случае мы снова получаем нулевой остаток, поэтому

Это также корень многочлена.

И мы продолжаем применять ту же процедуру. Теперь мы проверим, если

является ли это корнем многочлена или нет:

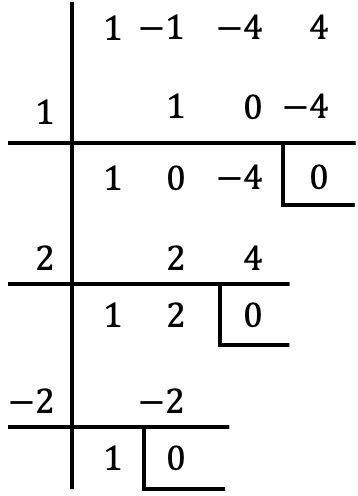
Разделив на

По правилу Руффини мы получаем нулевой остаток, поэтому

является корнем или нулем многочлена.

Поэтому мы больше не можем продолжать применять правило Руффини, поэтому мы уже нашли все корни многочлена, а именно:

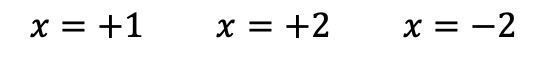
После того, как мы определили все корни многочлена, мы можем его факторизовать. Для этого просто выразим каждый корень

в виде фактора вида

, то есть для каждого корня необходимо поставить скобку с

и корень поменял знак:

И теперь, когда у нас есть все корни, выраженные в виде факторов, мы должны умножить все круглые скобки на коэффициент члена высшей степени исходного многочлена:

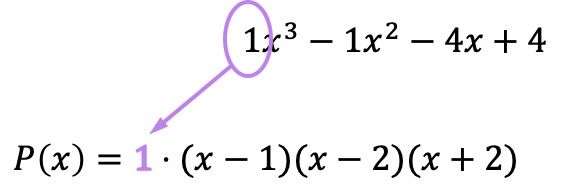
Хотя в данном случае коэффициент равен 1 и поэтому не влияет на результат, важно не забывать производить это умножение. Поскольку, если бы указанный коэффициент отличался от 1, факторизованный полином изменился бы и, следовательно, не введя число, мы допустили бы ошибку при факторизации многочлена.

Короче говоря, факторизованный полином:

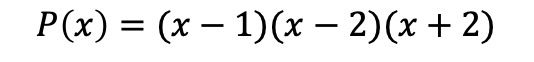
Факторизация полиномов без независимого члена

Мы только что увидели, что независимый член важен для факторизации многочленов, поскольку он позволяет нам идентифицировать возможные корни многочлена. Однако как факторизовать полином, у которого нет независимого члена?

Чтобы факторизовать многочлен без независимого члена , необходимо сначала извлечь общий фактор многочлена, а затем извлечь корни многочлена без общего фактора, используя правило Руффини.

Написанный так, это может показаться немного сложным, поэтому давайте шаг за шагом решим пример, чтобы вы могли увидеть, как факторизовать полином с общим множителем:

• Выполните факториальное разложение следующего полинома:

Как видите, у многочлена в задаче нет независимого члена, поэтому нам придется взять общий делитель многочлена. Если присмотреться, все элементы полинома имеют хотя бы один

поэтому общий фактор

Таким образом, при выделении общего множителя из многочлена мы получаем следующее выражение:

И как только мы извлекли общий делитель многочлена, мы применяем правило Руффини для вычисления корней многочлена, сгруппированных в скобках (с помощью процедуры, которую мы видели в предыдущем разделе):

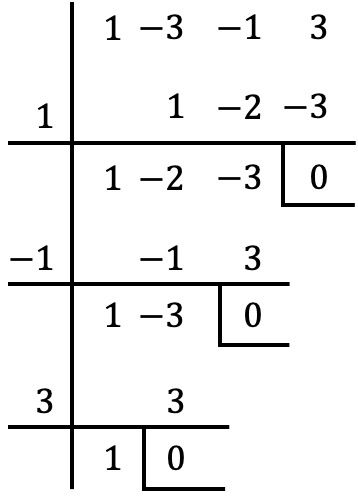
Таким образом, корни или нули полинома в скобках равны:

Поэтому, чтобы факторизовать полином, просто замените полином в скобках его корнями в факторной форме (как описано в разделе выше):

И таким образом мы уже факторизовали полином, у которого не было члена степени 0. Обратите внимание, что единственное отличие состоит в том, что сначала нам нужно извлечь общий множитель, но все последующие шаги абсолютно одинаковы.

С другой стороны, вы должны знать, что

Это также корень многочлена, поскольку, когда мы извлекаем общий делитель, это означает, что один из корней многочлена равен

Итак, все корни многочлена имеют вид:

Фактически, многочлен должен иметь столько корней, сколько указывает его степень. В этом случае многочлен имеет степень 4 и, следовательно, имеет 4 корня.

Факторизация полиномов с рациональными корнями

До сих пор мы видели примеры факторизации многочленов с целыми корнями, однако многочлен может иметь и рациональные корни, то есть с дробями. Давайте посмотрим, как решается этот тип полиномиальной факторизации на примере:

• Умножьте следующий неполный полином:

Как всегда, мы используем правило Руффини с делителями независимого члена, чтобы попытаться определить корни многочлена:

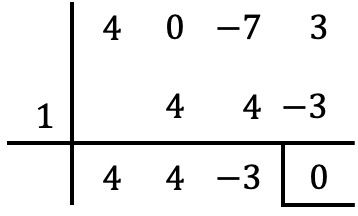
Но мы не можем вычислить больше корней с помощью Руффини, потому что, если мы попытаемся выполнить Руффини со всеми другими числами делителей независимого члена, мы получим остаток, отличный от нуля.

Таким образом, мы оказываемся в ситуации, когда только с

остаток от деления равен 0, это означает, что многочлен может иметь дробные корни. Для определения этих корней мы могли бы применить Руффини с дробями, однако в расчетах очень легко допустить ошибки, поэтому в этих случаях мы обычно делаем следующее:

Когда мы не можем продолжать применять правило Руффини с целыми корнями, мы должны приравнять последний полученный многочлен к 0 и решить полученное уравнение. Значит, корнями многочлена будут значения, найденные из уравнения.

С другой стороны, если уравнение не имеет решения, это означает, что многочлен больше не имеет корней и, следовательно, не может быть полностью факторизован.

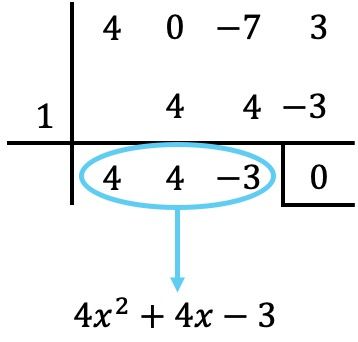
Поэтому мы устанавливаем фактор-полином равным нулю:

И для решения полученного уравнения используем формулу квадратного уравнения:

Таким образом, корни многочлена:

Таким образом, многочлен имеет корни в виде дробей.

И как только мы узнаем все корни многочлена, мы сможем легко найти факторизованный многочлен, выразив каждый корень

в виде фактора вида

, то есть для каждого корня необходимо поставить скобку с

и корень поменял знак:

Помните, что для факторизации многочлена необходимо также умножить его факторы на коэффициент члена высшей степени нефакторизованного многочлена, который в данном случае равен 4.

Особые случаи факторизации полиномов

Обычно для факторизации полинома используется правило Руффини (или синтетическое деление), как объяснено выше. Но в зависимости от полинома задачи иногда можно выполнить факторизацию полинома быстрее. Ниже мы рассмотрим каждый из этих частных случаев.

Учет известных личностей

Если мы видим, что полином соответствует заметному тождеству (или заметному произведению), его очень просто факторизовать. Однако, чтобы это сделать, вы должны освоить формулы для выдающихся личностей , в противном случае я рекомендую вам взглянуть на эту ссылку, где вы не только найдете формулы, но и сможете увидеть примеры выдающихся личностей. личности, и вы даже можете практиковать упражнения, решая их шаг за шагом.

Разница квадратов

Как известно, формула заметного тождества разности квадратов выглядит следующим образом:

Следовательно, если мы найдем полином, удовлетворяющий выражению

можно учитывать непосредственно.

Посмотрите на следующий пример, в котором учитывается разность квадратов:

С другой стороны, корни многочлена:

Другие примеры факторизации биномов, представляющих собой разность квадратов:

Сложение и вычитание квадрата

Вы уже должны знать формулы двух основных оставшихся примечательных тождеств: квадрата сложения и квадрата вычитания.

Итак, если мы поймем, что полином соответствует одному из этих двух примечательных тождеств, мы сможем факторизовать его напрямую. Посмотрите на следующие примеры:

Определить эти известные типы продуктов немного сложнее. Хитрость заключается в том, чтобы проверить, является ли независимый член многочлена квадратом некоторого числа, и является ли член более высокой степени квадратом монома (обычно

), в этом случае достаточно убедиться в справедливости того, что

равен окончанию промежуточного диплома.

Например, если у нас есть следующий полином:

В данном случае это может быть только квадрат суммы, поскольку все элементы многочлена положительны. Итак, переменная

формулы должно быть 5, так как оно является корнем независимого члена, а переменная

Это должно быть

, так как это корень термина может степень.

Осталось теперь доказать, что формула квадрата суммы выполняется с членом промежуточной степени:

✅

Формула значимого продукта удовлетворяется, поэтому факторизованный полином имеет вид:

И корень этого многочлена

который является двойным корнем, поскольку его фактор возведен в квадрат (повторяется дважды).

Ниже приведены дополнительные примеры факторизации идеальных квадратных трехчленов:

Факторизация трехчленов второй степени

Как мы только что видели, иногда встречаются трехчлены, которые представляют собой полные квадраты, и их можно непосредственно факторизовать с помощью формул для известных тождеств. Но большинство триномов не являются примечательными произведениями, так как же нам учитывать эти случаи полиномов?

Для факторизации квадратного многочлена не обязательно применять метод Руффини, достаточно приравнять многочлен к нулю и решить полученное квадратное уравнение. Таким образом, решения уравнения будут корнями многочлена.

Например, если нас попросят факторизовать следующий многочлен степени 2:

Вместо использования Руффини мы устанавливаем полином равным 0:

А теперь воспользуемся формулой уравнения 2-й степени, чтобы найти решения уравнения:

Таким образом, корни многочлена:

И, наконец, полиномиальная факторизация:

Факторизация трехчленов четвертой степени с четными показателями

Как и в предыдущем случае, чтобы факторизовать многочлен четвертой степени с четными показателями, нам нужно установить многочлен равным нулю и решить биквадратное уравнение. Чтобы найденные значения соответствовали корням многочлена.

В качестве примера факторизуем следующий полином 4-й степени:

Сначала установим полином равным нулю:

Теперь нам нужно решить биквадратное уравнение. Для этого сделаем изменение переменной:

Решаем квадратное уравнение по формуле:

Отменяем замену переменной для вычисления корней:

Таким образом, корни многочлена:

И как только мы узнаем корни или нули многочлена, мы факторизуем его, выражая его корни алгебраически в виде множителей:

Факторизация полиномов путем группировки

В некоторых особых случаях формула может использоваться для факторизации полинома особого типа.

Если у нас есть многочлен следующего вида:

Мы можем упростить полином, удалив общий делитель:

А полином можно еще больше упростить, выделив общий множитель второй раз:

Таким образом, мы смогли факторизовать полином, не применяя Руффини или какой-либо другой метод. И корни указанного многочлена будут:

Теперь давайте рассмотрим этот метод на числовом примере:

Сначала удалим общий делитель с

и с 2:

И как сейчас

является общим фактором полинома, мы извлекаем общий фактор полинома

Таким образом, корни многочлена:

Этот метод также называется факторизацией полиномов путем извлечения двойного общего фактора. Хотя это очень быстрая процедура, мы не рекомендуем выполнять этот тип факторизации, поскольку при факторизации с помощью этого метода часто возникают ошибки. Кроме того, как мы видели выше, многочлен степени 2 также можно факторизовать, решив простое квадратное уравнение. Короче говоря, ничего не получится, если вы плохо разбираетесь в этом методе.

Наконец, следует отметить, что существуют еще более сложные методы полиномиальной факторизации, такие как алгоритм LLL, метод Кронекера и метод Трагера, которые здесь не объясняются из-за их математической сложности.

Решенные упражнения на факторизацию многочленов

После того, как вы ознакомились со всеми типами факторизующих полиномов, мы рекомендуем вам попрактиковаться в решении упражнений. Вот почему мы подготовили ниже несколько пошаговых упражнений для факторизации полиномов. Помните, что если у вас есть вопросы, вы можете написать их в комментариях и мы быстро на них ответим.

Упражнение 1

Проведите факторизацию следующего полинома 3-й степени:

Это полный, упорядоченный полином третьей степени и в конечном итоге независимый. Поэтому мы применяем метод Руффини для определения корней многочлена:

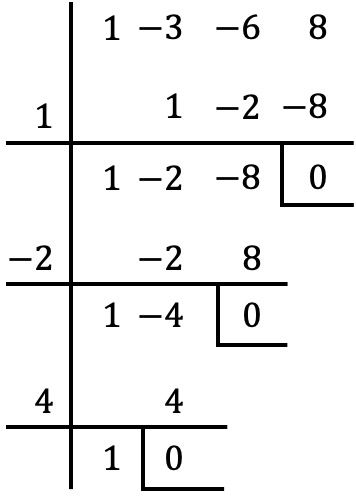
Таким образом, корни многочлена будут следующими:

Таким образом, полиномиальная факторизация такова:

Упражнение 2

Вычислите факторизацию следующего полинома 4-й степени:

Это многочлен четвертой степени и с независимым членом, поэтому мы используем метод Руффини, чтобы найти корни многочлена:

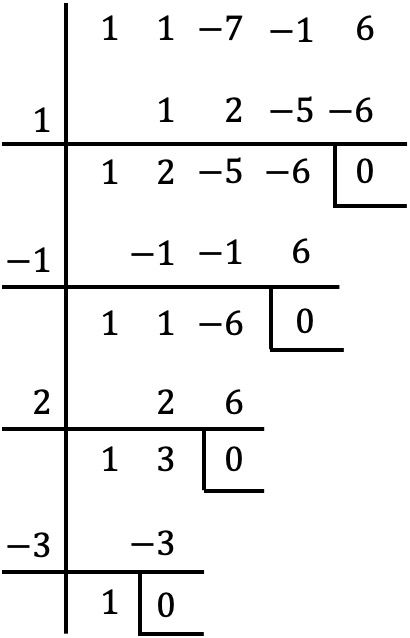
Таким образом, корни многочлена:

И когда мы факторизуем полином, у нас остается:

Упражнение 3

Найдите факторизацию следующего полинома четвертой степени:

В этом случае у полинома нет независимого члена, мы должны сначала извлечь общий множитель:

Теперь, когда мы взяли общий множитель x, вычислим корни или нули многочлена в скобках, используя метод Руффини:

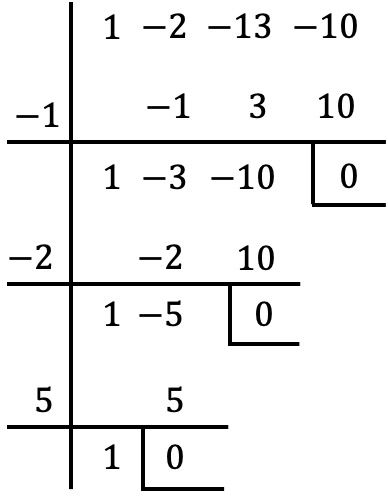
Таким образом, корнями многочлена являются те, которые мы нашли методом Руффини плюс x=0 общего множителя:

И наконец, разложив полином на множители, получим следующее выражение:

Упражнение 4

Преобразуйте следующий полином третьей степени в факторы:

Этот многочлен имеет независимый член, поэтому мы вычисляем его корни с помощью алгоритма Руффини:

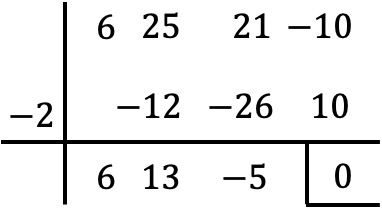
Однако когда мы достигнем этой точки, мы не сможем продолжать применять правило Руффини, поскольку без другого целого числа остаток от деления будет равен нулю.

Поэтому положим полученный полином равным нулю:

И для решения полученного уравнения применим формулу квадратных уравнений:

Таким образом, корни или нули многочлена равны:

Поэтому факторизацию многочлена необходимо производить с помощью дробей:

Упражнение 5

Определите факторизацию следующего полинома 6-й степени:

Полином в задаче не имеет независимого члена, поэтому сначала нужно извлечь общий множитель, который в данном случае равен

И как только мы удалим из многочлена общий делитель, мы найдем корни многочлена в скобках, используя правило Руффини:

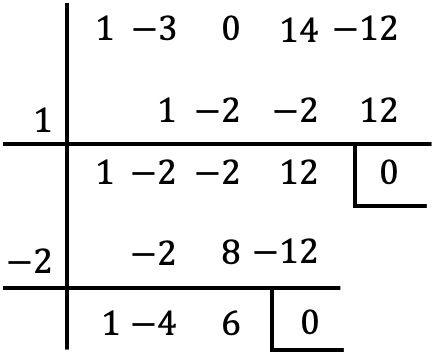
Но когда мы дойдем до этого этапа, мы не сможем продолжать двигаться вперед, потому что без другого целого числа остаток будет равен нулю.

Поэтому мы приравниваем полученный многочлен к нулю:

И решаем квадратное уравнение по формуле:

Корней из отрицательных чисел нет, поэтому уравнение не имеет решения, а это значит, что мы не можем найти больше корней многочлена. Другими словами, полином не является полностью факторизуемым.

Однако корни, которые нам удалось найти, таковы:

Обратите внимание, что корень

повторяется дважды, потому что мы удалили общий делитель из

а поскольку оно возведено в квадрат, это означает, что оно представляет собой двойной корень.

В заключение, факторизованный полином будет продуктом всех найденных корней, выраженных как факторы.

умножается на полином, полученный по правилу Руффини, который в дальнейшем нельзя учитывать:

Упражнение 6

Выполните факторизацию всех следующих полиномов:

Полином в разделе A) соответствует примечательному тождеству, а именно квадрату суммы. Следовательно, его факторизация такова:

Полином из раздела Б) также является примечательным произведением, в частности, это разность квадратов, поэтому:

Точно так же многочлен в разделе C) представляет собой примечательное равенство, в частности, он состоит из квадрата вычитания. Следовательно, его факторизация такова:

Наконец, полином в части D) не является примечательным тождеством. Поэтому мы должны установить многочлен равным 0 и решить полученное уравнение, чтобы найти его корни:

Используем формулу квадратного уравнения:

Таким образом, корни многочлена D) равны:

И, наконец, результат полиномиальной факторизации: