На этой странице объясняется, что такое факториал числа и как он рассчитывается. Кроме того, представлены несколько примеров и таблица значений наиболее используемых факториалов. Он также учит, как вычислить факториал числа с помощью калькулятора. И, наконец, проиллюстрировано применение и свойства факториалов.
Что такое факториал числа?
В математике факториал числа равен произведению всех натуральных чисел от 1 до этого числа. Кроме того, факториал числа обозначается восклицательным знаком (!) после числа.
Например, чтобы определить факториал числа n , также называемый факториалом n , необходимо умножить число n на все целые числа, которые ему предшествуют (начиная с единицы):
![]()
Как вычислить факториал числа
Разобравшись со значением факториала числа, давайте на примере посмотрим, как определить любой факториал:
- Вычислите факториал 4:
Как мы видели в математическом определении, факториал числа эквивалентен умножению всех натуральных чисел, меньших или равных ему. Следовательно, чтобы вычислить факториал 4, нам нужно умножить числа 1, 2, 3 и 4:
![]()
Таким образом, факториал 4 дает 24.
Примеры факториалов чисел
Чтобы завершить понимание понятия факториала числа, мы оставляем вам пример вычисления нескольких факториалов разных чисел:
- Факториал 3:
![]()
- Факториал 5:
![]()
- Факториал 6:
![]()
- Факториал 1:
![]()
Логически факториал числа 1 равен 1, так как достаточно умножить 1.
- Факториал 0:
![]()
Да, ладно, как ни странно, факториал 0 равен не нулю, а 1. Вам это может показаться немного странным, ведь по идее нужно умножать 0 на 1. Однако по соглашению принято, что 0! =1, поскольку свойство продукта пусто . Мы оставляем вам эту ссылку на случай, если вы захотите узнать больше, хотя не очень важно, чтобы вы знали причину, важно то, что вы помните, что факториал 0 равен 1 .
Список результатов для факториалов чисел
Ниже мы свели факториалы наиболее употребляемых чисел в таблицу, чтобы вам не пришлось вычислять их вручную.
| Номер | Факториал числа |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40,320 |
| 9 | 362 880 |
| десять | 3 628 800 |
| одиннадцать | 39 916 800 |
| 12 | 479 001 600 |
| 13 | 6 227 020 800 |
| 14 | 87 178 291 200 |
| пятнадцать | 1 307 674 368 000 |
| 16 | 20 922 789 888 000 |
| 17 | 355 687 428 096 000 |
| 18 | 6 402 373 705 728 000 |
| 19 | 121 645 100 408 832 000 |
| двадцать | 2 432 902 008 176 640 000 |
| пятьдесят | 3 041 409 320 · 10,64 |
| 100 | 9 332 621 544 · 10 157 |
| 1000 | 4 023 872 601 · 10,2567 |
| 10 000 | 2 846 259 681 · 10 35 659 |
| 100 000 | 2 824 229 408 · 10 45 6573 |
| 1 000 000 | 8 263 931 688 · 10 5 565 708 |
Факториал числа с помощью калькулятора
Как видно из предыдущих примеров, результаты факториалов двух последовательных чисел растут в геометрической прогрессии, поэтому узнать факториал больших чисел довольно сложно. Итак, мы покажем вам, как найти факториал числа с помощью калькулятора.
Научные калькуляторы имеют клавишу с символом x! или н! который используется для вычисления факториала целого числа. Итак, чтобы определить, сколько стоит факториал, необходимо выполнить на калькуляторе следующую последовательность действий:
![]()
Обычно калькуляторы CASIO имеют факторный ключ x! или н! над кнопкой x -1 .
В качестве примера мы решим факториал с помощью калькулятора, чтобы вы могли проверить, умеете ли вы это делать. Например, мы сделаем факториал 9:
![]()
Чтобы найти факториал 9, необходимо сначала ввести число 9, а затем нажать клавишу
![]()
и, наконец, нажмите кнопку равенства. В этом случае калькулятор должен показать нам результат 362 880.
Применение факториала
Функция факториала числа может показаться очень простой и абсурдной операцией, но в продвинутой алгебре она используется довольно часто. Затем мы увидим основные способы использования факториала.
Прежде всего, факториал — это важнейшая операция вычисления комбинаторного числа , более чем частная операция. Если вы не знаете, что такое комбинаторное число, посмотреть, из чего оно состоит и как рассчитывается, можно по этой ссылке, где вы найдете примеры, решенные упражнения и каковы его свойства. Кроме того, вы сможете увидеть, для чего он используется, поскольку он имеет множество реальных приложений.
Факториал также используется в математике для определения полинома Тейлора функции.
Аналогичным образом факториал используется для решения некоторых комбинаторных задач, в частности для вычисления комбинаций и перестановок. В этом смысле факториалы также часто используются для расчета вероятностей с использованием комбинаторики.
Перестановка из n элементов соответствует каждому из различных вариантов расположения этих элементов. Итак, для вычисления перестановки используется факториал. Например, если в задаче вы хотите найти количество возможностей, в которых можно расположить 7 объектов, вам необходимо вычислить факториал 7.
Теперь посмотрим на решенное упражнение:
- У нас есть 5 разных пар обуви, сколькими способами мы можем их расположить?
В этом упражнении нам предстоит найти все возможные способы объединения этих 5 пар обуви с учетом порядка их размещения. Итак, чтобы решить задачу, вам просто нужно вычислить факториал 5:
![]()
Короче говоря, 5 пар обуви можно разместить 120 различными способами.
Свойства факториала
Факториальное число имеет следующие характеристики:
- Если два положительных целых числа n и m такие, что n больше m , то, очевидно, значение факториала n больше, чем значение факториала m .
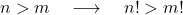
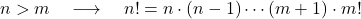
![]()
- Следующее алгебраическое выражение справедливо для факториала любого числа, кроме факториала 1:
![]()
Факториал отрицательного или десятичного числа
Мы только что увидели, как найти значение факториала положительного целого числа, но… можем ли мы вычислить факториал отрицательного или десятичного числа? Ответ — да, но необходимы глубокие знания математики.
Факториал отрицательного числа и десятичного числа вычисляется с помощью специальной функции, называемой «Гамма-функция Эйлера», которая определяется следующим интегралом:
![]()
Таким образом, любой тип факториала можно решить с помощью гамма-функции, поскольку всегда верно следующее уравнение:
![]()
Например, чтобы найти факториал 0,5, мы должны найти значение
![]()
потому что:
![]()
А решение интеграла будет соответствовать факториалу 0,5.
Очевидно, что решить интеграл от гамма-функции непросто, и мы не будем учить этому в этой статье, поскольку многие математические понятия придется объяснять заранее. Но мы хотели, чтобы вы знали, что существует возможность вычисления факториала отрицательного или десятичного числа.
Фактически, в качестве примера, мы вычислили некоторые отрицательные факториалы и десятичные значения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|