Уравнения первой степени или линейные уравнения являются основой алгебры , потому что, если вы их не понимаете, вам будет очень трудно понять более сложные уравнения. Итак, особенность этого типа уравнений состоит в том, что буквальная часть мономов не может иметь показатель степени. Следовательно, в линейном уравнении мы найдем только мономы без буквальной части и мономы с буквальной частью без показателя степени, например: 3 + x = -5 – 3x .
Также обратите внимание, что эти уравнения обычно имеют единственное решение, хотя может и не быть. Для того, чтобы узнать, какой случай перед нами, мы должны решить уравнение и в конце проанализировать результат . Итак, если мы получим невозможное равенство, например 2 = 0, то уравнение не имеет решения. С другой стороны, если мы получим равенство, которое всегда истинно, то решение будет эквивалентно всем действительным числам. И, наконец, если в конце мы получим равенство X и числового значения, в этом случае мы получим уникальный результат.
Процедура решения линейного уравнения
Решение уравнения эквивалентно вычислению значения переменной, обозначенной буквой (x, y, a, b…). Итак, чтобы найти это значение, нам нужно выполнить следующие шаги:
- Решите круглые скобки и дроби. Для начала мы удалим все круглые скобки и знаменатели, чтобы получить уравнение, которое будет легче понять. Поскольку мы можем напрямую оценить, какие термины сопровождаются неизвестным, а какие нет, такое прочтение позволяет нам легко продолжить решение выражения.
- Упростим выражение: группируем схожие термины (независимые термины с одной стороны и термины с x с другой стороны). Итак, на одной стороне мы оставим числа с неизвестным, а остальные числа передадим на противоположную сторону. Но помните: чтобы изменить их стороны, нам нужно изменить их знак.
- Действуем с каждой стороны: Все действия выполняем в следующем порядке: степени/корни, умножение/деление и сложение/вычитание. Мы делаем это до тех пор, пока не получим по одному члену с каждой стороны, и в итоге мы получим уравнение такой же структуры: 4x = 8.
- Изолируйте переменную: наконец, просто передайте значение, сопровождающее букву, путем деления на другую сторону, и мы таким образом найдем ее окончательное значение. В конце этого шага мы решим неизвестную проблему и узнаем, какой тип результата остается: уникальное решение, недопустимое решение или решение, удовлетворяющее всем целым числам.
Примеры уравнений первой степени
Ниже вы найдете решенные уравнения первой степени , которые сгруппированы в различные категории в зависимости от сложности их структуры. Итак, зная теоретическую процедуру решения линейных уравнений и существующие различные типы, у вас уже будут необходимые знания, чтобы легко их решать, и мы начнем с практики. Тем не менее, давайте начнем с теоретического объяснения:
Основные уравнения первой степени
Этот первый тип линейных уравнений состоит только из основных арифметических операций (сложение, вычитание, умножение и деление). Вот два рабочих примера: первый немного более простой, а второй немного более сложный с точки зрения вычислений:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
х = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
х = 3/2
Уравнения первой степени со скобками
Во-вторых, у нас есть линейные уравнения в скобках. Их решить немного сложнее, чем предыдущие, хотя их единственная трудность заключается в вычислении, поскольку необходимо учитывать свойства скобок. Чтобы было понятнее, покажем вам два отработанных примера:
2(х + 3) – 4х = -4
2х + 6 – 4х = -4
-2x = -10
х = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12х = -7х + 2
12х + 7х = -13 + 2
19x = -11
х = -11/19
Уравнения первой степени со степенями и корнями
Третий уровень довольно простой, так как он лишь добавляет силы и корни. Единственная трудность, с которой вы можете столкнуться при работе с этими уравнениями, — это когда показатель степени или корень влияет на целочисленную скобку (как во втором примере, который мы вам покажем), но все остальное остается практически таким же. Ниже приведены два примера.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2х = 8х + 4
14 – 2х = 8х + 4
-2x – 8x = -14 + 4
-10x = -10
х = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
х = -40
Уравнения первой степени с дробями
Последняя категория линейных уравнений, которую мы можем найти, состоит из всех элементов, которые мы прокомментировали ранее, а также из дробей. Этот уровень является самым сложным и существует несколько способов его решения. Первый и самый простой — умножить знаменатели на противоположную часть равенства, хотя мы можем использовать это только тогда, когда у нас есть две дроби. С другой стороны, если в уравнении более двух дробей, мы должны найти общий знаменатель и умножить все дроби, разделив это значение на знаменатель той же дроби. Ниже приведен пример каждого типа:
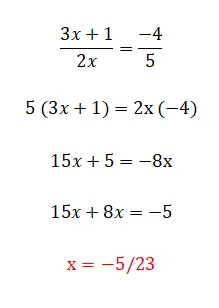
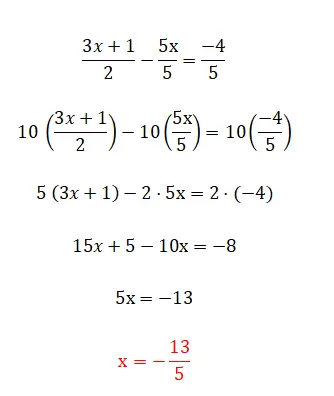
Упражнения по уравнениям первой степени
Теперь мы предлагаем несколько упражнений с линейными уравнениями. Они организованы по возрастающей сложности: первые уравнения проще последних. Поэтому мы рекомендуем вам начать с самого начала и посмотреть, как далеко вы сможете зайти. Итак, попробуйте решить следующие уравнения, а затем сравните свой результат с решениями, которые мы предлагаем.
Первое упражнение
Первое упражнение представляет собой очень простое линейное уравнение, поскольку оно состоит только из сложения и вычитания, а также имеет только четыре члена между двумя частями равенства:
2х – 3 = 4х + 5
2х – 4х = 5 + 3
-2x = 8
х = 8/(-2)
х = -4
- Мы группируем похожие термины вместе.
- Мы упрощаем обе стороны.
- Мы стираем неизвестное и вычисляем его ценность.
второе упражнение
В этом случае мы имеем уравнение, образованное круглыми скобками, и нашей главной задачей является их устранение, чтобы мы могли затем сгруппировать похожие члены вместе:
-4(х + 2) + 5х = 6 + 5х
-4x – 8 + 5x = 6 + 5x
-4х + 5х – 5х = 6 + 8
-4x = 14
х = 14/(-4) = -7/2
- Разбираем скобки.
- Мы перемещаем x влево, а независимые члены — вправо.
- Проясняем неизвестное.
Упрощаем результат.
третье упражнение
Далее вам нужно будет решить еще одно квадратное уравнение со скобками, хотя это немного сложнее. Это связано с тем, что в нем есть вложенные круглые скобки (круглые скобки внутри других скобок). Поэтому необходимо правильно соблюдать порядок разрешения: сначала инсайдеры, потом аутсайдеры.
3х + 2 (х – (4х – 5)) = 1 – (3 (2х + 7) – 2)
3х + 2 (х – 4х + 5) = 1 – (6х + 21 – 2)
3х + 2х – 8х + 10 = 1 – 6х – 21 + 2
-3x + 10 = -6x – 18
3х = -28
х = -28/3
- Начнем с решения внутренних скобок.
- Далее мы разрешаем внешние круглые скобки.
- Упрощаем обе части равенства и собираем аналогичные члены.
- Выделяем x и вычисляем его значение.
четвертое упражнение
В этом упражнении мы начинаем видеть дроби, которые, вероятно, являются самым сложным элементом линейных уравнений. Хотя не волнуйтесь, потому что если вы прочитали теорию, вы прекрасно будете знать, как это сделать:
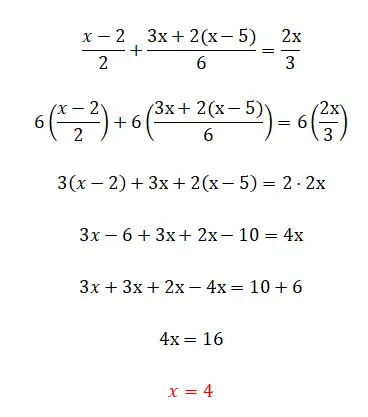
Пятое упражнение
В этом пятом упражнении мы видим дроби в скобках, а это означает, что иерархия решения становится немного сложнее. Стоит отметить, что данный пример можно решить двумя способами: методом наименьших общих кратных или непосредственно оперируя дробями. Ниже вы можете увидеть две полные процедуры:
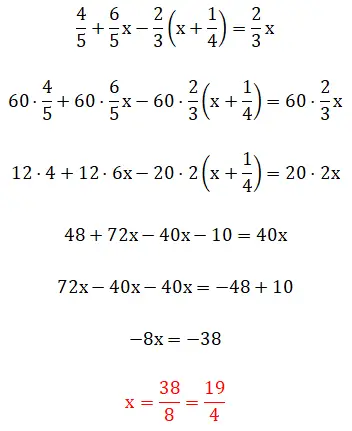
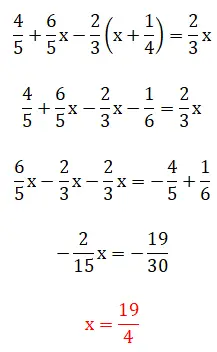
шестое упражнение
Далее мы пойдём немного дальше с темой дробей и круглых скобок, поскольку у нас есть вложенные круглые скобки. Это упражнение не приносит намного больше сложностей по сравнению с предыдущим, просто оно немного сложнее в плане расчетов и все.
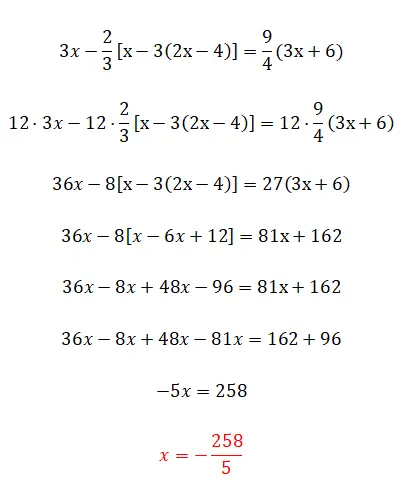
- Умножаем все слагаемые на lcmp знаменателей.
- Упростим выражение, убрав скобки: сначала те, что внутри, потом те, что снаружи.
- Сгруппируем схожие термины с каждой стороны.
- Решаем операции с каждой стороны.
- И мы вычисляем ценность неизвестного.
седьмое упражнение
Следующее упражнение может показаться очень простым, но мы все равно рекомендуем вам попробовать его решить, так как оно наверняка даст вам несколько необычный результат. Попробовав, посмотрите на решение и объяснение под упражнением.
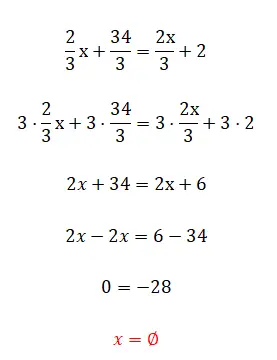
- Умножаем все дроби на Н.см знаменателей.
- Упростим полученное выражение.
- И, наконец, мы видим, что это дает нам ложное равенство, поскольку мы устранили неизвестное.
Как вы могли заметить, это ложное равенство или равенство без результата, поскольку не существует значения, которое правильно завершало бы уравнение. Это один из случаев, о которых мы упоминали во введении.
восьмое упражнение
Наконец, мы предлагаем вам это упражнение, которое довольно сложное, поскольку в нем есть все сложности, которые мы видели в этой статье, хотя есть и небольшая хитрость. Прокомментируйте: если вы можете решить это уравнение первой степени, то вы прекрасно поняли всю теорию. А если нет, не волнуйтесь, ведь это упражнение достаточно сложное.
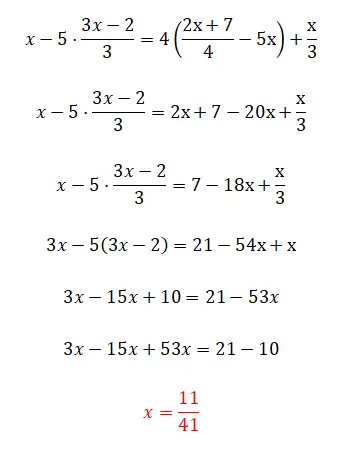
- Начнем с исключения четырех в правой части уравнения.
- Затем соединяем крестики с правой стороны.
- Умножаем все слагаемые на три, чтобы исключить знаменатели.
- Убираем скобки.
- Мы объединили схожие термины.
- Вычисляем значение неизвестного.
Дополнительные упражнения с линейными уравнениями
Теперь, когда у вас достаточно практики, вы сможете решать сложные линейные уравнения . Хотя, если вы хотите продолжить практику, мы рекомендуем вам попробовать решить этот рабочий лист . Но если вы считаете, что рассмотрели достаточно, мы также можем предложить вам статью, которая поможет вам понять иерархию операций . Таким образом, вы всегда будете знать, какой расчет нужно решить в первую очередь, и никогда не ошибетесь .