На этой странице вы найдете формулу уравнения точки-наклона линии, а также различные способы ее расчета. Кроме того, вы сможете увидеть несколько примеров и попрактиковаться в упражнениях, решаемых шаг за шагом.
Формула уравнения точки-наклона линии
Уравнение наклона точки линии — это способ математического выражения линии. В частности, вам нужны только наклон и координаты точки на линии, чтобы найти уравнение наклона точки на линии.
Формула уравнения точки-наклона линии выглядит следующим образом:
![]()
Золото
![]()
это наклон линии и
![]()
это координаты точки на прямой
![]()
Давайте посмотрим , как рассчитывается уравнение точки-наклона линии на примере:
- Напишите уравнение угла наклона прямой, проходящей через точку.
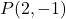
и уклон m=3.
Формула уравнения точки-наклона линии выглядит следующим образом:
![]()
В этом случае утверждение сообщает нам, что наклон линии равен m=3, поэтому уравнение линии будет следующим:
![]()
Кроме того, мы также знаем, что прямая проходит через точку
![]()
, поэтому мы должны подставить координаты этой точки в уравнение:
![]()
![]()
Таким образом, уравнение наклона точки линии имеет вид:
![]()
Имейте в виду, что помимо уравнения точки-наклона, существуют и другие способы аналитического выражения линии: векторное уравнение, параметрические уравнения, непрерывное уравнение, неявное уравнение (или общее) и явное уравнение линии. Если вас больше интересует, вы можете проверить, что представляет собой каждый из них, на нашем сайте.
Что означает наклон линии?
Как мы видели в определении уравнения точки-наклона линии, параметр
![]()
это наклон линии. Но на самом деле… что означает наклон линии? Давайте посмотрим на это на графическом представлении линии:
Наклон линии указывает на ее крутизну. Как видно из линии графика,
![]()
равно 2, так как линия поднимается на 2 единицы по вертикали за 1 единицу по горизонтали.
Очевидно, что если наклон положителен, функция возрастает (уходит вверх), а если наклон отрицательный, функция убывает (уменьшается).
Как рассчитать наклон линии
Кроме того, существует три различных способа численного определения наклона линии:
- Даны две разные точки на прямой

И

Наклон линии равен:
- Ага

– вектор направления линии, ее наклон:
- Ага

— угол, образованный линией с осью абсцисс (ось X), наклон линии эквивалентен тангенсу указанного угла:
![]()
![]()
![]()

Относительное положение линий
Наконец, наклон линии также используется для определения взаимосвязи между несколькими линиями. Поскольку две параллельные линии имеют одинаковый наклон и, с другой стороны, если наклон одной линии является отрицательной величиной, обратной наклону другой линии, это означает, что эти две линии перпендикулярны .


Вычислите уравнение наклона точки линии, проходящей через две точки.
Очень распространенной проблемой является определение уравнения наклона точки по двум точкам, принадлежащим прямой. Давайте посмотрим, как она решается на примере:
- Найдите уравнение наклона точки линии, проходящей через следующие две точки:
![]()
Чтобы найти уравнение наклона точки линии, нам нужно определить, каков наклон линии. Итак, мы вычисляем наклон линии, используя формулу двоеточия:
![]()
Таким образом, уравнение наклона точки линии будет следующим:
![]()
![]()
Поэтому нам нужно лишь подставить в уравнение декартовы координаты точки на прямой:
![]()
![]()
![]()
Также хорошо, если мы поместим другую точку утверждения в уравнение линии:
![]()
![]()
Найдите уравнение наклона точки линии по графику
Как мы видели в разделах выше, существует несколько способов численного нахождения уравнения наклона точки линии. Однако его можно найти и графически. Давайте посмотрим, как это делается, на примере:
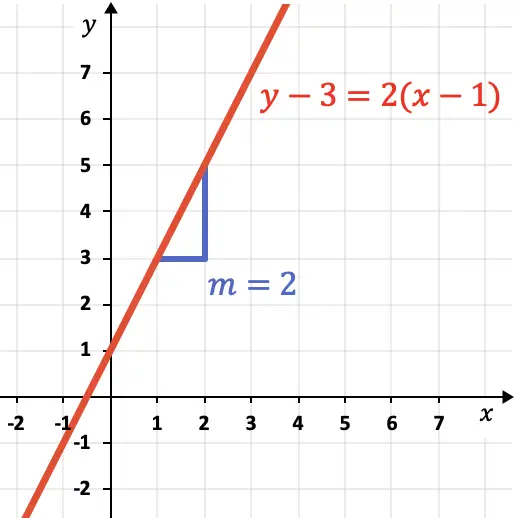
- Определите уравнение наклона точки для линии, показанной на следующем графике:
Чтобы определить уравнение наклона точки для нарисованной линии, нам необходимо найти ее наклон и точку на линии.
В данном случае наклон линии равен 3, поскольку линия поднимается на 3 вертикальные единицы на каждую горизонтальную единицу.
![]()
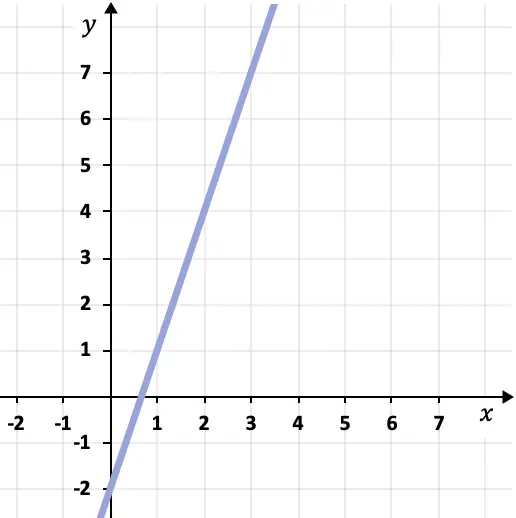
Далее нам нужна точка на линии. Для этого мы можем выбрать любую точку на графике, через которую проходит линия, например точку (1,1).
![]()
Следовательно, теперь мы можем найти уравнение наклона точки линии, применив его формулу:
![]()
![]()
Решенные задачи уравнения точки-наклона
Упражнение 1
Напишите уравнение угла наклона прямой, проходящей через точку.
![]()
и его наклон
![]()
Формула уравнения точки-наклона линии:
![]()
В этом случае утверждение сообщает нам, что наклон линии равен m=-2, поэтому уравнение линии будет следующим:
![]()
Кроме того, из утверждения мы также знаем, что прямая проходит через точку
![]()
, поэтому достаточно подставить координаты точки в уравнение прямой:
![]()
![]()
Упражнение 2
Каково уравнение угла наклона линии, проходящей через следующие две точки?
![]()
Чтобы найти уравнение наклона точки линии, нам нужно определить, каков наклон линии. Поэтому мы рассчитываем наклон линии по ее формуле:
![]()
Таким образом, уравнение наклона точки линии будет следующим:
![]()
![]()
Поэтому нам нужно лишь подставить в уравнение координаты точки на прямой:
![]()
![]()
Было бы также правильно включить в уравнение и другую точку утверждения:
![]()
Упражнение 3
Найдите уравнение наклона точки линии, проходящей через следующие две точки:
![]()
Чтобы найти уравнение наклона точки линии, необходимо сначала вычислить ее наклон:
![]()
Таким образом, уравнение наклона точки линии будет следующим:
![]()
![]()
Поэтому нам нужно лишь подставить в уравнение координаты точки на прямой:
![]()
![]()
![]()
Также правильно поставить другую точку в утверждении в уравнение прямой:
![]()
Упражнение 4
Рассчитайте уравнение наклона точки для линии, которая образует угол 45° с осью X и проходит через начало координат.
Если линия составляет угол 45 градусов с осью OX, ее наклон составит:
![]()
![]()
![]()
И как только мы узнаем наклон линии, мы сможем найти уравнение наклона точки, подставив в уравнение точку на линии. Кроме того, оператор сообщает нам, что линия проходит через начало координат, а это значит, что она проходит через точку (0,0). Еще:
![]()
![]()
Таким образом, уравнение наклона точки линии имеет вид:
![]()
Упражнение 5
Найдите уравнение наклона точки прямой, параллельной прямой.
![]()
и что происходит через точку
![]()
быть прямым
![]()
![]()
Наклон линии
![]()
равно 2 (число перед круглыми скобками), и чтобы две линии были параллельными, они должны иметь одинаковый наклон, следовательно:
![]()
![]()
И как только мы узнаем наклон линии, мы просто подставляем в формулу координаты точки, принадлежащей линии:
![]()
![]()
Таким образом, уравнение наклона точки линии имеет вид:
![]()
Упражнение 6
Определите уравнение наклона точки для каждой линии, показанной на следующем графике:

синий правый
Синяя линия увеличивается на один Y для каждого X, поэтому ее наклон равен 1. С другой стороны, она проходит через точку (2,4), поэтому:
![]()
прямо зеленый
Зеленая линия увеличивается на три Y для каждого X, поэтому ее наклон равен 3. Кроме того, одна из ее точек равна (2,2), поэтому:
![]()
Красная линия
Красная линия уменьшается на два Y для каждого X, поэтому ее наклон равен -2. И точка (0,-2) принадлежит этой линии, поэтому:
![]()