Здесь вы найдете объяснение разрешения всех типов известных личностей (или известных продуктов). Вы сможете увидеть, каковы формулы всех известных тождеств, а также примеры и упражнения, решаемые шаг за шагом. Кроме того, мы покажем вам, для чего используются эти знаменитые математические правила.
👉👉 Ниже мы шаг за шагом объясняем каждое примечательное тождество, но если вы предпочитаете, вы можете перейти непосредственно к таблице 😉, где сведены все формулы . 👈👈
Что такое известные личности (или известные продукты)?
Замечательные тождества , также называемые замечательными произведениями или замечательными равенствами , представляют собой математические правила, которые позволяют напрямую решать операции с многочленами.
Наиболее распространенными известными формулами тождества являются квадрат суммы , квадрат разности (или вычитания) и сумма, умноженная на разность .

Но ниже мы не только научим вас рассчитывать эти примечательные произведения, но и покажем вам все существующие типы примечательных тождеств.
Известные формулы (или продукты) идентичности
Как только мы увидим определение примечательных произведений (или примечательных равенств), мы увидим, каковы формулы для примечательных тождеств. С другой стороны, если вас интересуют демо-версии формул, вы можете просмотреть их формулы, нажав кнопку «Просмотреть демо».
квадрат суммы
Квадрат суммы или сумма в квадрате — одно из важнейших примечательных тождеств. Точнее, это бином с двумя положительными членами в степени 2, то есть его алгебраическое выражение равно (a+b) 2 .
Итак, формула квадрата суммы:

Если мы начнем с положительного бинома, повышенного до 2:
![]()
Математически квадрат выше эквивалентен множителю
![]()
умноженное само на себя:
![]()
Итак, умножаем многочлены, используя распределительное свойство:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Из четырех полученных слагаемых
![]()
И
![]()
похожи, поэтому мы можем сгруппировать их:
![]()
Настолько, что мы уже пришли к выражению формулы квадрата суммы, для которой она выводится:
![]()
Любопытно, что развитие выражения этого типа замечательного продукта называется идеальным квадратным трехчленом.
Так что квадрат суммы равен квадрату первого члена плюс удвоенное произведение первого на второе плюс квадрат второго.
Таким образом, чтобы решить квадрат суммы, недостаточно возвести каждое сложение к обоим, но, кроме того, два сложения необходимо умножить друг на друга и на 2. Важно помнить об этом, потому что очень типичная ошибка такого типа. продукта Примечательно забыть этот термин.

Пример:
- Вычислите следующее примечательное тождество, применив соответствующую формулу:
![]()
Как мы только что видели, формула примечательного равенства квадрата суммы такова:
![]()
Поэтому нам необходимо сначала определить параметры
![]()
И
![]()
формулы. В этом случае,
![]()
представляет собой
![]()
пары и
![]()
соответствуют номеру 5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Итак, теперь, когда мы знаем значения
![]()
и из
![]()
мы можем использовать формулу квадрата положительного бинома, чтобы найти результат:

квадрат разницы
Квадрат разницы , или квадрат разницы , — еще одно из трех наиболее часто используемых примечательных тождеств. В частности, он соответствует биному, образованному положительным членом и другим отрицательным членом, возведенным в число 2, то есть его алгебраическое выражение равно (ab) 2 .
Итак, формула квадрата разности (или квадрата вычитания) выглядит следующим образом:

Из биномиального выражения квадрата вычитания:
![]()
Очевидно, предыдущая степень равна произведению множителя
![]()
умноженное само на себя:
![]()
Теперь умножим две скобки, применив распределительное свойство:
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
Поэтому вам просто нужно сгруппировать похожие термины вместе, чтобы завершить проверку формулы:
![]()
Тогда формула квадрата разности доказывается математически:
![]()
Так что квадрат разности равен квадрату первого слагаемого минус удвоенное произведение первого на второе плюс квадрат второго.
Что касается замечательного равенства квадрата суммы, то нельзя забыть поставить средний член формулы, так как следующее уравнение неверно:

Пример:
- Решите следующее примечательное равенство квадрата разности:
![]()
Это заметный продукт квадратичного вычитания, поэтому необходимо применить соответствующую формулу:
![]()
Далее мы должны определить, каковы значения неизвестных.
![]()
И
![]()
формулы. В этом случае,
![]()
это переменная
![]()
И
![]()
соответствуют номеру 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
Обратите внимание, что отрицательный знак не является частью параметра
![]()
но для правильного применения этой формулы всегда нужно брать число без знака.
Таким образом, мы уже знаем значения
![]()
и из
![]()
, поэтому достаточно подставить эти значения в формулу, чтобы разрешить заметное тождество:

сумма по разнице
Произведение суммы и разности — одно из трех наиболее часто используемых известных тождеств. Как следует из названия, это положительный бином, умноженный на сопряженный с ним бином (тот же бином, но с измененным промежуточным знаком), то есть алгебраическим выражением этого типа замечательного произведения является (a +b) · (ab) .
Формула замечательного тождества произведения суммы на разность такова:

Начиная с произведения суммы на вычитание любых двух слагаемых:
![]()
Чтобы продемонстрировать формулу, нам просто нужно умножить первую скобку на вторую, используя распределительное свойство:
![Rendered by QuickLaTeX.com \begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-346d3d7ca4da1e71fad52c84a33ef4fc_l3.png)
Теперь сгруппируем похожие термины вместе:
![]()
И таким образом мы добились выражения замечательного равенства. Таким образом, демонстрируется формула этого замечательного типа идентичности:
![]()
Таким образом, произведение суммы на разность двух величин равно разности квадратов этих величин. Другими словами, умножение суммы двух разных слагаемых путем вычитания этих двух слагаемых эквивалентно возведению каждого из двух слагаемых в квадрат и их вычитанию.
Пример:
- Найдите, используя соответствующую формулу, следующее примечательное произведение суммы на разность двух разных слагаемых:
![]()
Как мы видели выше, формула заметного равенства суммы, умноженной на разность, выглядит следующим образом:
![]()
Прежде всего, что нам нужно сделать, это определить значения букв
![]()
И
![]()
формулы. В этом случае
![]()
соответствуют переменной
![]()
И
![]()
соответствуют номеру 2.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-87b76b09924467ba75f033336e6a18e5_l3.png)
И когда мы уже знаем, какие значения принимают параметры
![]()
И
![]()
Применим формулу произведения суммы на разность:
квадрат трехчлена
Квадрат трехчлена (многочлена, состоящего из трех членов) равен квадрату первого члена плюс квадрат второго члена плюс квадрат третьего члена плюс удвоенное значение первого на второе плюс удвоенное первое на третье, плюс дважды второе за третье.

Из любого трехчлена в квадрате:
![]()
Квадрат выше можно разложить на трехчлен, умноженный сам на себя:
![]()
Теперь решаем полиномиальное умножение:
![]()
И, наконец, группируем схожие термины:
![]()
Таким образом, мы уже пришли к выражению формулы, поэтому демонстрируется формула квадрата трехчлена:
![]()
Пример:
- Найдите следующее примечательное равенство:
![]()
Формула квадрата трехчлена:
![]()
Как и во всех известных равенствах, сначала необходимо определить значения неизвестных в формуле. В этом упражнении
![]()
Восток
![]()
коэффициент
![]()
соответствуют
![]()
И
![]()
является независимым членом 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55e06f44486e75e9153a60d36e83bc37_l3.png)
А когда мы уже знаем значения, просто подставляем эти значения в формулу и производим расчеты:

Известные личности (или продукты) в кубе
Мы только что изучили все примечательные тождества в квадрате, то есть все типы примечательных тождеств, образованные степенями, возведенными в степень 2. Что ж, теперь мы собираемся проанализировать примечательные тождества в кубе. Конечно, формулы кубической идентичности немного сложнее, но они тоже очень полезны.
куб суммы
Заметным кубическим произведением суммы является бином (многочлен только с двумя мономами) в степени 3, два элемента которого положительны. Следовательно, алгебраически куб суммы выражается как (a+b) 3 .
Формула заметного равенства куба суммы:

Начиная с положительного бинома в кубе:
![]()
Вышеупомянутую мощность можно разложить на произведение множителя
![]()
по площади:
![]()
Аналогично, как мы видели в известных квадратичных равенствах, биномиальное
![]()
Ее можно решить по формуле квадрата суммы:
![]()
Затем мы умножаем два многочлена вместе:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06771ecbb13542eae2a68477f849d729_l3.png)
Наконец, нам просто нужно сгруппировать похожие термины вместе:
![]()
Таким образом, проверяется формула примечательного тождества суммы бинома в кубе:
![]()
Короче говоря, сумма, возведенная в число 3, равна кубу первого плюс трижды квадрат первого на второй, плюс трижды первый на квадрат второго плюс куб второго.
Пример:
- Решите следующее примечательное тождество кубической суммы, используя соответствующую формулу:
![]()
В этой задаче мы имеем бином степени 3, два члена которого положительны. Поэтому мы должны использовать формулу для кубической суммы:
![]()
Теперь нам нужно найти значения параметров
![]()
И
![]()
формулы. В этом случае,
![]()
соответствуют переменной
![]()
И
![]()
это номер 2.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-909b3b4a2f976c165f160a6765b3ed9d_l3.png)
С помощью которого мы вычисляем знатное произведение, заменяя значения
![]()
и из
![]()
в формуле:

куб разницы
Куб разности , или куб вычитания , представляет собой бином степени 3, имеющий член с отрицательным знаком. Итак, математическое выражение для этого замечательного типа продукта: (ab) 3 .
Формула куба разности (или вычитания):

Очевидно, доказательство этой формулы очень похоже на доказательство примечательного произведения суммы, возведенной в куб. Но в данном случае мы начинаем с отрицательного кубического бинома:
![]()
Ясно, что предыдущее потенцирование можно разложить на произведение множителя
![]()
умноженный на его квадрат:
![]()
Итак, как мы изучали известные квадратичные тождества, бином
![]()
Его можно рассчитать по формуле квадрата разницы:
![]()
Теперь мы производим произведение двух полиномов:
![Rendered by QuickLaTeX.com \begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-627a273de8fff974f4a14a32fcee90b8_l3.png)
И последний шаг — сгруппировать похожие термины:
![]()
Таким образом, проверяется формула примечательного тождества вычтенного бинома, возведенного в куб:
![]()
Таким образом, разница (или вычитание), увеличенная до трех, равна кубу первого минус три раза квадрат первого на второй плюс три раза первый на квадрат второго минус куб второго.
Пример:
- Вычислите следующий кубический бином (разность), используя соответствующую формулу:
![]()
В этом упражнении у нас есть пара с положительным элементом и отрицательным элементом. Поэтому мы должны использовать формулу кубической разности:
![]()
Сначала, как всегда, определяем значения неизвестных.
![]()
И
![]()
формулы. В этом случае
![]()
представляет собой моном
![]()
И
![]()
является независимым членом бинома, т.е. 2.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a792ec6dead8466ec6a2cb2a43d9fab4_l3.png)
Обратите внимание, что параметр
![]()
просто равно 2, без отрицательного знака числа. Важно помнить об этом, чтобы правильно применять формулу.
Наконец, мы находим замечательное тождество, помещая значения
![]()
и из
![]()
в формуле:

Сводная таблица известных личностей
Подводя итог, мы составили таблицу со всеми примечательными личностями (или продуктами), которые мы видели, чтобы вам было легче их изучить. 😉

Решенные упражнения с известными личностями (или продуктами)
Чтобы вы окончательно поняли понятие замечательных тождеств, также называемых замечательными произведениями или замечательными равенствами, мы подготовили несколько упражнений, решаемых шаг за шагом. Вы можете попробовать их выполнить, а затем проверить, хорошо ли вы справились с решениями упражнений.
⬇⬇ Не забывайте, что все интересующие вас вопросы вы можете задать нам ниже в комментариях! ⬇⬇
Упражнение 1
Раскройте следующие примечательные тождества (суммы квадратов):
![]()
![]()
![]()
![]()
Все заметные тождества в задаче представляют собой суммы в квадратах, поэтому в этом случае мы всегда должны применять одну и ту же формулу:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-067fdf38612ca481db587bda479cab24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Упражнение 2
Разработайте следующие примечательные продукты (разницы в квадрате):
![]()
![]()
![]()
![]()
Все известные произведения в этом упражнении представляют собой вычитания в квадрате, поэтому нам нужно применить только одну формулу:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
Упражнение 3
Разработайте следующие примечательные равенства (произведения сумм на разности):
![]()
![]()
![]()
![]()
Поскольку все известные равенства в этом упражнении представляют собой умножение сумм на разности, все они решаются по одной и той же формуле:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-826c4aec8f005514a14cdc8555c084c4_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6793239af84413fb9408c2cb6033e5ce_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-630b94cf4be27c5f7b9c87651368634d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80c5451e407a2c0e670c6cb22a74043c_l3.png)
Упражнение 4
Решите все следующие известные личности:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c65875e01d82840e30ae85d803d45e90_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04e0bcf5df362d320cfdb2f87cdc6ddc_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc3f7dc61f7c44a60c01e0a95de278fa_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4d4a0c86d26820881eb65cb92c3679a_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-432c4ae0f050bec15e3fa52f426698ec_l3.png)
Упражнение 5
Рассчитайте следующие заметные продукты:
![]()
![]()
![]()
![]()
Чтобы найти все примечательные произведения задачи, необходимо применить формулы суммы и разности, возведенных в куб по случаям:
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14695fb807e2df89352fdd1c1dced2ee_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5be0d584351feb0bef5572ca5c9e159a_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44f9c3283dad97321644c6e559f64ff_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-156e7619e4d6ef129f04250af8197d2e_l3.png)
Упражнение 6
Решите следующие известные равенства:
![]()
![]()
![]()
![]()
Чтобы решить все эти известные тождества, нам нужно использовать формулу квадрата трехчлена, которая имеет вид:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-749dc45e7a00d7122d62b774706bdcc0_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1f51f18b3c1118b6e8e3acc3441b0ec_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49c6496bf684296d315fc96d9cb5857e_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cd08035d8402c27c411bcf5b30216cb_l3.png)
Упражнение 7
Вычислите следующие известные тождества с корнями и дробями (высокая сложность):
![]()
![]()
![]()
![]()
Раздел А) состоит из вычитания в квадрате, поэтому для его решения необходимо применить соответствующую ему формулу и, кроме того, нужно помнить, что если корень возвести в квадрат, то он упрощается:
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-999e71bf062ea313780439abaf2b4295_l3.png)
Раздел Б) посвящен сложению вычитанием и одночлены имеют дробные коэффициенты, с которыми это знатное произведение необходимо определить, используя формулу сложения вычитанием и свойства дробей:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24593bac7bd4a9837e1f18fef4f9c38e_l3.png)
Примечательное равенство в разделе C) представляет собой сумму, возведенную в 2, и также состоит из дробей. Поэтому для его расчета нам нужно воспользоваться формулой суммы в квадрате плюс свойства дробей:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Последнее примечательное тождество касается суммы, умноженной на разность, с иррациональными коэффициентами, поэтому мы применяем формулу для суммы, умноженной на разницу, а затем упрощаем квадратные корни:
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c540e4315e9e84faaa2ff656c4eec21_l3.png)
Другие известные типы идентичности
Все известные личности, которые мы обсуждали выше, являются наиболее часто используемыми. Однако в математике есть и другие известные типы продуктов, о которых также интересно знать, поскольку они используются для разных целей.
сумма кубов
Сумма кубов соответствует биному, два члена которого положительны и, кроме того, его кубические корни точны. Следовательно, алгебраическим выражением суммы кубов является a 3 +b 3 .

Формула этого примечательного произведения используется для факторизации многочлена, то есть с помощью формулы мы преобразуем многочлен в произведение бинома на трехчлен.
Итак, вы можете увидеть, как это делается, вот пример применения этого замечательного тождества:
![]()
Действительно, предыдущее выражение состоит из сложения кубов, поскольку кубический корень монома
![]()
является точным (не дает десятичное число), и число 8 тоже:
![]()
![]()
![]()
Следовательно, мы можем использовать формулу суммы совершенных кубов, чтобы преобразовать кубическое выражение в произведение бинома на трехчлен:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f30ea5f0f7ef1b89a16f1d00e54d063c_l3.png)
разница кубов
Разность (или вычитание) кубов представляет собой бином, состоящий из положительного члена и отрицательного члена, кубические корни которого точны. Другими словами, разность кубов выражается в виде a 3 -b 3 .

Давайте приведем пример, чтобы вы могли увидеть, как разрешается этот замечательный тип идентификатора:
![]()
Это разность кубов, потому что кубический корень монома
![]()
как 27 верно:
![]()
![]()
![]()
Поэтому вы можете использовать формулу разности идеальных кубов для факторизации бинома:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-342a448f849bf2856ad9a5394733faeb_l3.png)
Произведение биномов с общим членом
Этот примечательный продукт используется для преобразования произведения двух биномов, имеющих общий член, в квадратичный многочлен.

Вот подробный пример такого замечательного продукта:
![Rendered by QuickLaTeX.com \begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8447db6a2246c09b2e7be29f8050a3d6_l3.png)
больше личностей
Хотя известные личности являются наиболее известными, поскольку они наиболее распространены, следует отметить, что существует также больше личностей с другими именами. Вот список других менее известных личностей, если вам интересно:
- Тождества Лагранжа:
-
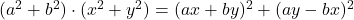
-
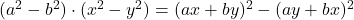
- Личности Лежандра:
-
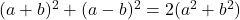
-
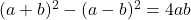
-
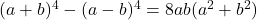
- Личность Арганда:
-
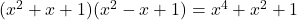
- Гауссовы тождества:
-
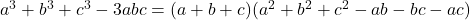
-
![Rendered by QuickLaTeX.com a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6b2da7d99ade85355a54bee45b79a9f_l3.png)
Известные приложения для идентификации
Если вы зашли так далеко, значит, вы уже умеете выполнять вычисления с известными личностями. Яркий! Но на самом деле… для чего нужны примечательные личности? И когда используются известные личности?
Как мы видели в этой статье, основная цель заметных тождеств — упростить вычисления. То есть благодаря замечательным продуктам мы можем напрямую решать определенные степени комплексных многочленов, не выполняя сложных операций.
Но у примечательных равенств есть и другие функции, такие как факторизация многочленов и завершение квадратов. Затем мы посмотрим, из чего состоит каждое из этих приложений.
Факторинг полиномов
Некоторые очень специфические типы полиномов можно факторизовать с заметными тождествами. Например, если мы находим многочлен, состоящий из двух членов, которые являются полными квадратами (их квадратные корни точны), мы можем факторизовать его, используя замечательную формулу равенства произведения суммы на разность:
![]()
![]()
Аналогичным образом, трехчлены, которые учитывают примечательные тождества квадрата сложения или вычитания, могут быть факторизованы:
![]()
![]()
![]()
![]()
Аналогично, после факторизации многочлена можно найти корни (или нули) этого многочлена. Тем не менее, эту концепцию немного сложнее понять, поэтому, если вам это интересно, мы рекомендуем поискать объяснение в поисковой системе на нашем сайте (вверху справа), так как у нас есть целая статья, объясняющая это.
квадратное завершение
Завершение квадратов — это математическая процедура, используемая для преобразования квадратного трехчлена в сумму квадрата плюс (или минус) числа.
Учитывая любой трехчлен:
![]()
Тогда трехчлен можно преобразовать в следующее выражение:
![]()
где параметры
![]()
И
![]()
рассчитываются по следующим формулам:
![]()
Даже если вам это не кажется, эти две формулы выведены из известных личностей. Итак, благодаря замечательным изделиям, квадраты можно доукомплектовать.
В качестве примера мы применим эту процедуру к следующему трехчлену:
![]()
Рассчитаем параметры
![]()
И
![]()
![]()
![]()
И, следовательно, полином остается:
![]()