В этой статье вы найдете определение теоремы Вейерштрасса. Кроме того, вы сможете попрактиковаться в нескольких упражнениях, шаг за шагом решая теорему Вейерштрасса, чтобы в совершенстве понять ее.
Формулировка теоремы Вейерштрасса
Теорема Вейерштрасса гласит, что если функция непрерывна на замкнутом интервале, эта функция имеет на этом интервале абсолютный максимум и абсолютный минимум.
➤ См.: Что такое непрерывная функция?
Теорема Вейерштрасса лишь утверждает, что существует максимум и минимум, но вычислять значения этих точек бесполезно.
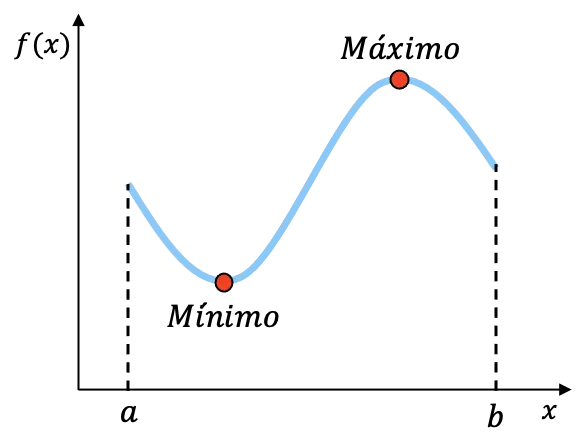
Например, функция, изображенная выше, непрерывна на интервале [a,b] и имеет минимум и максимум на этом интервале. Хотя мы не можем знать точные координаты этих двух точек, мы знаем, что функция имеет эти две конечные точки на интервале.
➤ См.: как вычислить максимум и минимум функции
Поскольку функция непрерывна на всем интервале, это означает, что она также будет принимать все возможные значения между абсолютным минимумом и абсолютным максимумом на этом же интервале.
Кроме того, как следствие теоремы Вейерштрасса, можно вывести, что любая непрерывная функция на отрезке ограничена сверху и снизу , а верхняя и нижняя границы функции являются абсолютным максимумом и минимумом соответственно.
Математически теорему Вейерштрасса можно выразить следующим образом:
Золото
И
две включенные точки (абсолютный минимум и абсолютный максимум соответственно) в замкнутом интервале
![[a,b]](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
в котором определена функция.
Доказательство теоремы Вейерштрасса довольно сложное и не вносит особого вклада в концепцию, поэтому мы не будем объяснять его в этой статье. Важно то, что вы понимаете, что такое теорема Вейерштрасса и для чего она используется.
Теорема Вейерштрасса Решаемые задачи
Упражнение 1
Определите, ограничена ли следующая функция на предложенном интервале:
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e6a705ea1c5d586cf31d683ac7ccc85_l3.png "Rendered by QuickLaTeX.com")
➤ См.: область определения логарифмической функции.
Определить, ограничена ли функция на отрезке [5,10], можно, применив теорему Вейерштрасса. Поэтому мы должны знать, непрерывна ли функция в этом интервале, для этого мы вычисляем область определения логарифмической функции:
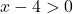
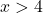
Функция непрерывна для всех значений больше x=4, поэтому она непрерывна на интервале [5,10].
Следовательно, функция удовлетворяет теореме Вейерштрасса об отрезке [5,10], что означает, что она ограничена сверху и снизу на этом отрезке.
Упражнение 2
Определите, имеет ли следующая функция максимум и/или минимум на предложенном интервале:
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f2e72f629bae2c39821ddbfbf6c93fc_l3.png "Rendered by QuickLaTeX.com")
➤ См.: область определения рациональной функции.
Сначала проанализируем непрерывность рациональной функции:
Однако функция имеет разрыв в точке x=2, что означает, что она не является непрерывной на интервале [-3,3].
Короче говоря, функция не удовлетворяет теореме Вейерштрасса, и поэтому мы не можем сказать, имеет ли она минимум или максимум в этом интервале.
Упражнение 3
Определите, имеет ли следующая функция максимум и/или минимум в предложенном интервале, и вычислите эти точки:
![f(x)=x^2+3 \qquad x \in [0,4]](https://mathority.org/wp-content/ql-cache/quicklatex.com-4dd0cf4151f8b5c1b4e69be89b7a71e1_l3.png "Rendered by QuickLaTeX.com")
➤ См.: характеристики квадратичных функций.
Областью определения любой квадратичной функции являются все действительные числа:
Таким образом, функция непрерывна на интервале [0,4] и удовлетворяет теореме Вейерштрасса. Таким образом, функция имеет абсолютный минимум и абсолютный максимум на этом интервале.
Более того, вершина этой параболы находится точно в точке x=0, поэтому функция строго возрастает на интервале [0,4] и, следовательно, минимум находится в точке x=0, а максимум в точке x= 4.
Карл Вейерштрасс
Как только мы поймем, что означает теорема Вейерштрасса, мы кратко объясним, кто был автором этой теоремы.
Карл Теодор Вильгельм Вейерштрасс был очень важным немецким математиком XIX века, точнее, он родился 31 октября 1815 года в Остенфельде и умер 19 февраля 1897 года в Берлине.
Помимо теоремы Вейерштрасса, он также известен своими другими вкладами в математику. Среди них он дал определения непрерывности, предела и производной — трех очень важных понятий функций.
Точно так же ему удалось продемонстрировать некоторые теоремы, которые в то время еще не были математически проверены, такие как теорема Больцано-Вейерштрасса, теорема о среднем значении или теорема Гейне-Бореля.
В качестве диковинки есть лунный кратер и астероид, названные в честь Вейерштрасса в его честь.