На этой странице вы найдете, что такое скалярная матрица, и несколько примеров скалярных матриц для полного понимания. Дополнительно вы сможете увидеть все свойства скалярных матриц и преимущества выполнения операций с ними. Наконец, мы объясним, как вычислить определитель скалярной матрицы и как инвертировать этот тип матрицы.
Что такое скалярная матрица?
Скалярная матрица — это диагональная матрица , в которой все значения на главной диагонали равны.
Это определение скалярной матрицы, но я уверен, что его лучше понять на примерах: 😉
Примеры скалярных массивов
Пример скалярной матрицы порядка 2×2
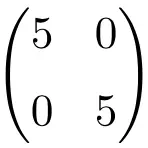
Пример скалярной матрицы 3×3
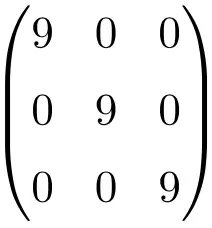
Пример скалярной матрицы размером 4×4
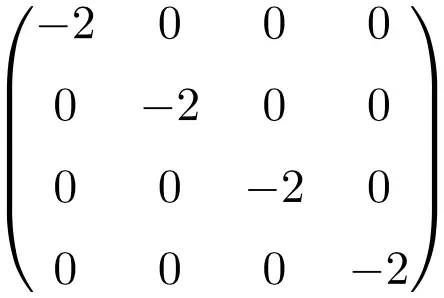
Свойства скалярных матриц
Скалярная матрица также является диагональной матрицей, поэтому вы увидите, что она наследует многие характеристики этого класса матриц:
- Все скалярные матрицы также являются симметричными матрицами .
- Скалярная матрица — это одновременно верхняя треугольная матрица и нижняя треугольная матрица .
- Единичная матрица является скалярной матрицей.
- Любая скалярная матрица может быть получена из произведения единичной матрицы и скалярного числа.
![Rendered by QuickLaTeX.com 4 \cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b77f7d177c2769b0847de258adfd1386_l3.png)
- Нулевая матрица также является скалярной матрицей.
- Собственные значения (или собственные значения) скалярной матрицы — это элементы ее главной диагонали. Поэтому их собственные значения всегда будут одинаковыми и будут повторяться столько раз, сколько размерность матрицы.
![Rendered by QuickLaTeX.com \begin{pmatrix} 8 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \longrightarrow \ \lambda = 8 \ ; \ \lambda = 8 \ ; \ \lambda = 8](https://mathority.org/wp-content/ql-cache/quicklatex.com-2513b8d4aeb6d932d9870934102a1637_l3.png)
- Сопряженным скалярной матрицей является другая скалярная матрица. И более того, значения главной диагонали присоединенной матрицы всегда будут такими же, как у исходной матрицы, возведенной в порядок матрицы — 1 .
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \longrightarrow \text{Adj}(A)=\begin{pmatrix} 5^{3-1} & 0 & 0 \\[1.1ex] 0 & 5^{3-1} & 0 \\[1.1ex] 0 & 0 & 5^{3-1} \end{pmatrix}= \begin{pmatrix} 25 & 0 & 0 \\[1.1ex] 0 & 25 & 0 \\[1.1ex] 0 & 0 & 25 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f7e94cc5a528abace04016dc263c8f9_l3.png)
Операции со скалярными матрицами
Одной из причин, по которой скалярные матрицы так широко используются в линейной алгебре, является простота, с которой они позволяют выполнять вычисления. Вот почему они так важны в математике.
Итак, давайте посмотрим, почему так легко выполнять вычисления с квадратной матрицей этого типа:
Сложение и вычитание скалярных матриц
Складывать (и вычитать) две скалярные матрицы очень просто: достаточно сложить (или вычесть) числа на главных диагоналях. Например:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} +\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix} = \begin{pmatrix} 7& 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-761de4b4c9bdbbc835b366b21d8cfc2d_l3.png)
Скалярное матричное умножение
Подобно сложению и вычитанию, чтобы решить задачу умножения или матричного произведения двух скалярных матриц, просто умножьте элементы диагоналей между ними. Например:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \cdot\begin{pmatrix} 6 & 0 & 0 \\[1.1ex] 0 & 6 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 12 & 0 & 0 \\[1.1ex] 0 & 12 & 0 \\[1.1ex] 0 & 0 & 12 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d30acbf9c6ad31625f8253549e659b02_l3.png)
Степень скалярных матриц
Вычислить степень скалярной матрицы тоже очень просто: нужно возвести каждый элемент диагонали в показатель степени. Например:
*** QuickLaTeX cannot compile formula:
\displaystyle\left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}\right.^4=\begin{pmatrix} 2^ 4 & 0 & 0 \\[1.1ex] 0 & 2^
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \right. inserted.
leading text: \end{document}
& 0 \\[1.1ex] 0 & 0 & 2^4 \end{pmatrix}= \begin{pmatrix} 16 & 0 & 0 \\[1.1ex] 0 & 16 & 0 \\[1.1ex] 0 & 0 и 16 \end{pmatrix}
![]()
\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7 \cdot 7 \cdot 7 = \bm {343}
![]()
\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7^3= \bm{343}
![Démontrer ce théorème est très simple : il suffit de calculer le déterminant d'une matrice scalaire par blocs (ou cofacteurs). Vous trouverez ci-dessous la <strong>démonstration</strong> de la formule utilisant une matrice scalaire générique :» title=»Rendered by QuickLaTeX.com» height=»62″ width=»1060″ style=»vertical-align: -4px;»></p>
<p> \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & a & 0 \\[1.1ex] 0 & 0 & a \end{vmatrix}& = a \cdot \begin{ vmatrix} a & 0 \\[1.1ex] 0 & a \end{vmatrix} – 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & a \end{vmatrix} + 0 \cdot \ начало{vmatrix} 0 & a \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (a\cdot a) – 0 \cdot 0 + 0 \cdot 0 \\[ 2ex] & = a \cdot a \cdot a \\[2ex] & = a^3 \end{aligned}</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-d24f9aa91fc9fe8ed74f705f83be3b32_l3.png)
![]()
а^3
![car la matrice est d'ordre 3, mais il faut toujours l'élever à l'ordre de la matrice.
<div class="adsb30" style=" margin:12px; text-align:center">
<div id="ezoic-pub-ad-placeholder-118"></div>
</div>
<h2 class="wp-block-heading"> Inverser une matrice scalaire</h2>
<p> Une matrice scalaire <strong>est inversible si, et seulement si, tous les éléments de la diagonale principale sont différents de 0</strong> . Dans ce cas on dit que la matrice scalaire est une matrice régulière. De plus, l’inverse d’une matrice scalaire sera toujours une autre matrice scalaire avec les <strong>inverses</strong> de la diagonale principale :» title=»Rendered by QuickLaTeX.com» height=»174″ width=»1250″ style=»vertical-align: -5px;»></p>
<p> \displaystyle A= \begin{pmatrix} 9 & 0 & 0 \\[1.1ex] 0 & 9 & 0 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} \ \longrightarrow \ A^{-1 }=\begin{pmatrix} \frac{1}{9} & 0 & 0 \\[1.1ex] 0 & \frac{1}{9} & 0 \\[1.1ex] 0 & 0 & \frac{ 1}{9} \end{pmatrix}</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-49f5afdd3e1e9918f5323139662a2138_l3.png)
![]()
\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}=\cfrac{1}{8} = $0,125