В этой статье мы объясняем, что такое симметричные функции (четные и нечетные функции) и как изучать симметрию функции. Вы также сможете увидеть свойства этих типов функций и, наконец, сможете попрактиковаться в упражнениях, решающих шаг за шагом симметричные функции.
Что такое симметричная функция?
Симметричная функция — это функция, у которой в ее графическом представлении можно найти ось симметрии. Существует два типа симметричных функций: четные функции, симметричные относительно оси Y, и нечетные функции, симметричные относительно начала координат.
Помните, что ось симметрии — это воображаемая линия, которая делит что-либо на две части так, что их противоположные точки находятся на равном расстоянии друг от друга.
даже функции
Четные функции — это функции, симметричные относительно оси Y, то есть ось Y является осью симметрии функции.
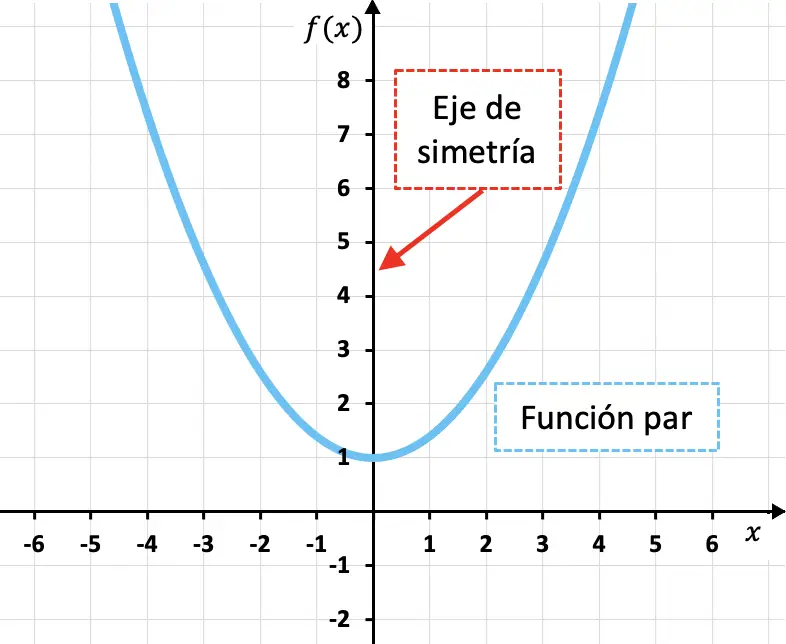
Как видно из приведенной выше квадратичной функции, образ четной функции для любого значения независимой переменной (x) эквивалентен образу функции для противоположного значения (-x). Другими словами, математически функция является четной, если она удовлетворяет следующему условию:
![]()
Четные функции — это разновидность симметричных функций, теперь давайте посмотрим, как выглядят нечетные функции.
нечетные функции
Нечетные функции — это функции, симметричные относительно начала координат, то есть относительно точки (0,0).
Ниже вы можете увидеть график странной функции:
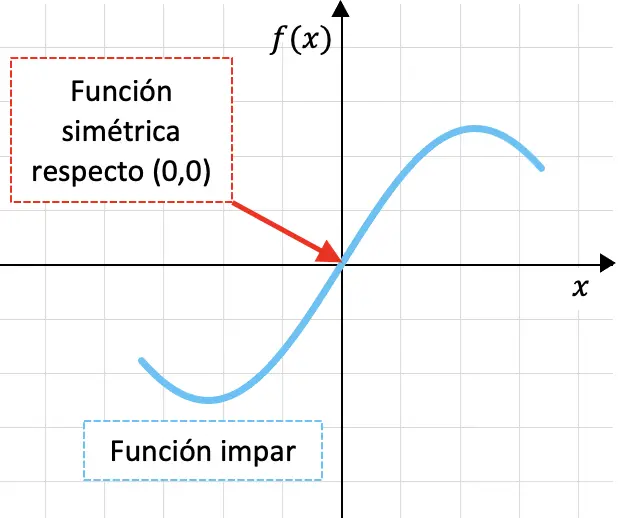
Тот факт, что функция симметрична относительно начала координат, означает, что если мы свернем график функции сначала через ось OY, а затем через ось OX, график функции перекроется.
С алгебраической точки зрения функция является нечетной, если между ее изображениями выполняется следующее соотношение:
![]()
Знание симметрии функции очень полезно для ее представления, поскольку, зная только одну половину графика, мы можем быстро нарисовать другую часть.
Как найти симметрию функции
Для изучения симметрии функции необходимо вычислить образ
![]()
, то есть необходимо вычислить
![]()
Итак, в зависимости от результата изображения симметрия функции будет:
- если он заполнен
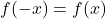
, функция четная и, следовательно , симметричная относительно оси Y.
- если он заполнен
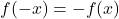
, функция нечетная и, следовательно , симметричная относительно начала координат.
- Если ни одно из вышеперечисленных условий не выполнено, это асимметричная функция (не имеет оси симметрии).
Например, давайте проанализируем симметрию следующей кубической функции:
![]()
Для изучения симметрии функции вычислим
![]()
![]()
Полученное алгебраическое выражение эквивалентно исходному выражению функции, но изменило знак, или, другими словами, выполняется следующее равенство:
![]()
Таким образом, функция нечетна и, следовательно, симметрична относительно начала координат (0,0).
Свойства симметричных функций
Симметричные функции имеют следующие характеристики:
- Сумма двух четных/нечетных функций равна другой четной/нечетной функции.
- Произведение двух четных функций или двух нечетных функций дает четную функцию.
- Производная четной/нечетной функции является четной/нечетной функцией.
- Композиция двух четных/нечетных функций эквивалентна четной/нечетной функции.
- Единственная функция, которая является одновременно четной и нечетной, то есть симметричной относительно оси OY и относительно начала координат, — это функция
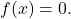
Решенные задачи симметрии функции
Упражнение 1
Найдите симметрию следующей функции:
![]()
Чтобы вычислить симметрию функции, нам нужно оценить
![]()
![]()
Любая степень отрицательного числа, возведенная в показатель степени, дает положительное число, поэтому в этом случае верно следующее уравнение:
![]()
Таким образом, функция четная и, следовательно, симметричная относительно оси Y (оси Y).
Упражнение 2
Изучите симметрию следующей рациональной функции:
![]()
Чтобы определить симметрию функции, сделаем
![]()
![]()
В этой задаче условие симметрии не выполняется, поскольку образ
![]()
не равен
![]()
ни для
![]()
![]()
Таким образом, функция не имеет оси симметрии, а является скорее асимметричной функцией.
Упражнение 3
Вычислите симметрию следующей функции:
![]()
Для анализа симметрии функции нам необходимо вычислить
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
В этом случае полученное выражение похоже на исходное выражение, но с изменением знака, поэтому выполняется следующее уравнение:
![]()
Таким образом, функция нечетна и, следовательно, симметрична относительно начала координат (0,0).