Расстояние между двумя линиями в пространстве (в r3)

На этой странице вы узнаете, как рассчитывается расстояние между двумя линиями в пространстве (в R3), независимо от их типа (параллельные, секущие, совпадающие, секущие, перпендикулярные линии и т. д.). Кроме того, вы сможете увидеть примеры и упражнения, решаемые шаг за шагом.

Как рассчитать расстояние между двумя линиями

Расстояние между двумя линиями — это минимальное расстояние между любой точкой одной линии и любой точкой другой линии. Это расстояние соответствует длине отрезка, идущего от одной линии к другой и одновременно перпендикулярного обеим линиям.

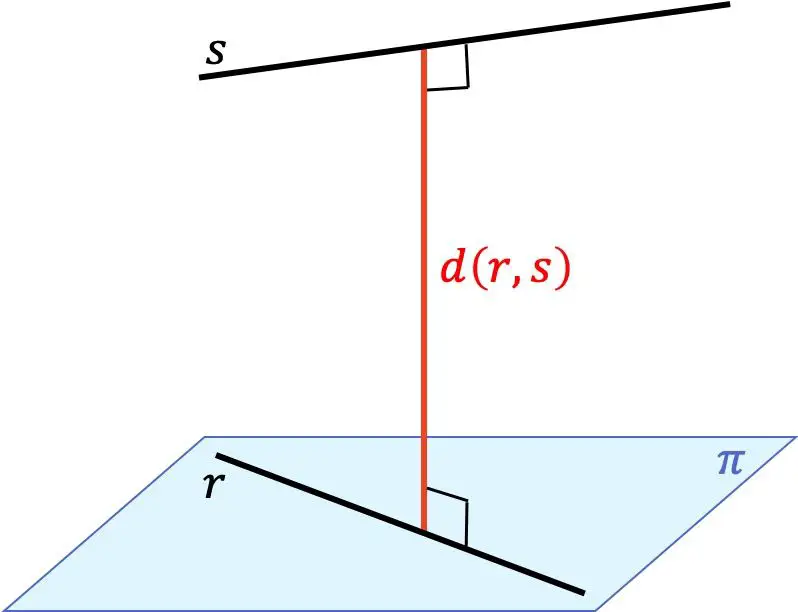
расстояние между двумя линиями в пространстве (в R3)

Итак, нахождение расстояния между двумя разными линиями в трехмерном (3D) пространстве зависит от взаимного положения между ними:

  • Если две линии совпадают или пересекаются , расстояние между двумя линиями равно нулю, поскольку они пересекаются (по крайней мере) в одной точке.
  • Когда две линии параллельны , нам нужно взять любую точку на одной из линий и вычислить расстояние между этой точкой и другой линией (ниже приведен пример того, как это сделать).
  • Если две линии пересекаются в пространстве, нам нужно применить формулу расстояния между двумя пересекающимися линиями (подробное объяснение см. Ниже).

Итак, чтобы вычислить расстояние между двумя линиями, необходимо сначала знать, какого типа эти линии, а затем, в зависимости от случая, использовать ту или иную формулу. Поэтому важно, чтобы вы уже научились находить взаимное положение двух линий в пространстве, прежде чем продолжить, но если вы не помните, как это было сделано, по ссылке вы увидите очень полное объяснение, а также примеры и решенные упражнения. шаг за шагом.

Как найти расстояние между двумя параллельными линиями в пространстве

Вычисление расстояния между двумя параллельными прямыми в пространстве (в R3) производится так же, как и в плоскости (в R2): необходимо взять точку на любой из двух прямых и найти расстояние этой точки на другой. линия.

расстояние между двумя параллельными линиями в пространстве

Таким образом, формула для расчета расстояния от точки до линии в трех измерениях (которая используется для определения расстояния между двумя параллельными линиями):

d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}

Золото:

  • \lvert \vv{\text{v}}_r \rvert

    — величина вектора направления линии

    r.

  • Q

    это точка на линии

    r,

    P

    точка на линии

    s

    И

    \vv{QP}

    вектор, определяемый двумя точками

  • \lvert \vv{QP} \times \vv{\text{v}}_r \rvert

    — величина векторного произведения между векторами

    \vv{QP}

    И

    \vv{\text{v}}_r

В качестве примера мы собираемся решить задачу о расстоянии между двумя параллельными линиями в пространстве:

  • Каково расстояние между следующими двумя параллельными прямыми?

r: \ (x,y,z) = (2,1,1) + t(-1,3,2)

s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)

Обе линии выражаются в виде векторного уравнения, поэтому мы легко узнаем вектор направления и точку каждой из них:

\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}

Если у вас есть сомнения относительно того, как определить вектор направления и точку прямой, рекомендуем взглянуть на объяснение уравнения прямой . Там мы объяснили это для всех уравнений прямой, поскольку нахождение вектора направления и точки, принадлежащей прямой, зависит от типа уравнения, в котором выражается линия.

Теперь, чтобы найти расстояние между двумя параллельными прямыми, нам нужно применить формулу расстояния от точки до прямой:

d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}

Итак, с одной стороны, мы вычисляем модуль вектора, полученного в результате векторного произведения. Если у вас есть сомнения относительно того, как оно рассчитывается, вы можете обратиться к формуле векторного произведения , где, кроме того, вы сможете увидеть примеры и решенные упражнения этой операции между векторами.

\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)

\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}

\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}

И, с другой стороны, находим величину вектора прямой

r:

\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}

Наконец, подставляем значение каждого слагаемого в формулу и вычисляем расстояние между строками:

d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}

Следовательно, расстояние между двумя линиями составляет 3,60 единицы.

Как определить расстояние между двумя пересекающимися линиями в пространстве

Как мы видели вначале, метод определения расстояния между двумя пересекающимися прямыми отличается от процедуры определения расстояний между параллельными прямыми.

расстояние между пересекающимися линиями в пространстве

Таким образом, существует несколько методов определения расстояния между двумя пересекающимися линиями в пространстве. На этой странице мы объясним только одну процедуру, самую простую, потому что два других метода более длительны и сложны, фактически они практически не используются.

Пусть вектор направления и любая точка двух пересекающихся прямых будут:

\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}

Формула расстояния между двумя пересекающимися линиями :

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Золото

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|

— абсолютное значение смешанного произведения векторов

\vv{\text{u}}, \vv{\text{v}}

и вектор, определяемый точками

A

И

B

. И с другой стороны,

\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert

— это амплитуда векторного произведения векторов направления двух пересекающихся линий.

Чтобы вы увидели, как определить расстояние между двумя пересекающимися линиями, на примере решим задачу:

  • Каково расстояние между двумя следующими пересекающимися прямыми?

r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}

s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}

Во-первых, нам нужно определить вектор направления и точку на каждой линии. Две линии выражаются в виде непрерывного уравнения, поэтому:

\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}

А теперь применим формулу расстояния между двумя пересекающимися линиями:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

С одной стороны, мы решаем смешанное произведение (или тройное скалярное произведение):

\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13

И, с другой стороны, находим модуль векторного произведения (или перекрестного произведения):

\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}

\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}

Наконец, подставляем значение каждого слагаемого в формулу расстояния между двумя пересекающимися линиями:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх