На этой странице вы увидите, как рассчитать рейтинг таблицы на основе параметра. Вы также найдете пошаговые примеры и решенные упражнения о том, как найти диапазон матрицы по одному параметру.
Чтобы полностью понять процедуру изучения ранга матриц с параметрами, важно, чтобы вы уже знали , как вычислять ранг матрицы по определителям . Поэтому мы рекомендуем вам сначала изучить эти две вещи, прежде чем продолжить чтение.
Как вычислить диапазон массива на основе параметра. Пример:
- Определяет диапазон матрицы A на основе различных значений параметров.
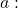
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0aa5688f2845a0225149f448466c943c_l3.png)
Матрица A будет иметь не более 3-го ранга, поскольку это матрица 3-го порядка. Поэтому первое, что нам нужно сделать, это решить определитель всей матрицы 3х3 с помощью правила Сарруса , чтобы посмотреть, может ли он иметь ранг 3:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-835a881061438326519f4660b4c394fc_l3.png)
Результат определителя является функцией параметра
![]()
. Поэтому мы устанавливаем результат равным 0, чтобы увидеть, когда таблица будет иметь ранг 2, а когда — ранг 3:
![]()
И решаем полученное уравнение:
![]()
![]()
![]()
Поэтому, когда
![]()
независимо от того, равно ли это +1 или -1, определитель 3×3 будет равен 0 и, следовательно, ранг матрицы не будет равен 3. С другой стороны, когда
![]()
отличается от +1 и -1, определитель будет отличен от 0 и, следовательно, матрица будет иметь ранг 3.
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-53dde6f61dc01cac5c0a0705c44a7433_l3.png)
Как мы видели ранее, когда
![]()
равно 1, определитель матрицы равен 0. Поэтому он не может иметь ранг 3. Теперь мы попытаемся вычислить определитель 2 × 2, отличный от 0, внутри матрицы, например, в верхнем левом углу:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d291f322f9d3f392e46568817e531a84_l3.png)
Определитель второго порядка отличен от 0. Таким образом, при параметре
![]()
или +1, ранг матрицы будет равен 2:
![]()
Как только мы увидим диапазон матрицы, когда
![]()
и когда
![]()
Давайте посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f723d9c6b9f786b8c405ac7ec2d8bf1d_l3.png)
Как мы видели вначале, когда
![]()
es -1, а определитель матрицы равен 0. Поэтому ему нельзя присвоить ранг 3. Поэтому следует попытаться встретить в матрице определитель 2×2, отличный от 0, например нижний часть матрицы. ЛЕВЫЙ:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdc9bd6d9ad083e1e38f53079aebb5e5_l3.png)
Определитель размерности 2 отличен от 0. Таким образом, при параметре
![]()
или -1, ранг таблицы будет равен 2:
![]()
Таким образом, мы нашли 3 различных случая, в которых ранг матрицы A зависит от значения, которое принимает параметр.
![]()
Вот резюме :
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc3a7ebea32c871ab7971a276decc60a_l3.png)
Теперь, когда вы знаете, как обсуждать диапазон матриц, зависящих от параметров, вы можете попрактиковаться в выполнении приведенных ниже пошаговых упражнений. Для их решения вам наверняка помогут свойства определителей , поэтому, если вы не очень разбираетесь в них, советую сначала заглянуть на связанную страницу, где каждый из них поясняется примерами.
Исправлены проблемы с диапазоном матриц на основе параметров.
Упражнение 1
Изучите диапазон следующей таблицы на основе значения параметра.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d7f53b08bcf2e2660dbb7c0aeb6fd369_l3.png)
Матрица A будет иметь не более ранга 3, поскольку это матрица 3×3. Следовательно, первое, что нам нужно сделать, это решить определитель всей матрицы (с помощью правила Сарруса), чтобы увидеть, может ли он иметь ранг 3:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2539698cbcf9f06d2890d17da76174f_l3.png)
Мы устанавливаем результат равным 0, чтобы увидеть, когда массив будет иметь ранг 2, а когда — 3:
![]()
![]()
![]()
Поэтому, когда
![]()
отлично от 2, определитель 3×3 будет отличен от 0 и, следовательно, ранг матрицы будет равен 3.
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c131e19dd5d5c0d7826306103b4e118b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-b97f01989b5e9679f95d300cd64f3735_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-77b38ebf03b8ed059edefd523c5ca1f4_l3.png)
![]()
Таким образом, мы обнаружили 2 случая, в которых диапазон матрицы A меняется в зависимости от значения, которое принимает параметр:
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-41e5cc7b6e9b3204f26e1c64e46f7057_l3.png)
Упражнение 2
Найдите диапазон следующей таблицы на основе значения параметра.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b28f21cc2e7211d9dae9b6685b541fc_l3.png)
Матрица A будет иметь не более ранга 3, поскольку это матрица 3×3. Следовательно, первое, что нам нужно сделать, это решить определитель всей матрицы (с помощью правила Сарруса), чтобы увидеть, может ли он иметь ранг 3:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-30c8c16fea09001059a5d66727fc7be3_l3.png)
Мы устанавливаем результат равным 0, чтобы увидеть, когда массив будет иметь ранг 2, а когда — 3:
![]()
![]()
![]()
![]()
![]()
Поэтому, когда
![]()
отличается от +1 и -1, определитель 3×3 будет отличаться от 0 и, следовательно, ранг матрицы будет равен 3.
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b95d408f076c4978c8605380a277cdf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcd50b9549925b5011a6c20943c326ee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03242296f208e07b9c4d634f0b7724cc_l3.png)
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2d16421400df26760d811229215ac83_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ecd0b86cd6c59a0911f0c39ca7599806_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-378e43f0ef61ccabf82dacb5ac70466f_l3.png)
![]()
Таким образом, мы обнаружили 3 случая, в которых диапазон матрицы A меняется в зависимости от значения, которое принимает параметр:
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bf1904cee51914e041d94f588fed84d_l3.png)
Упражнение 3
Вычисляет диапазон следующей таблицы на основе значения параметра.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-090a99d3b4111785433e5c769589eb01_l3.png)
Матрица A будет иметь не более ранга 3, поскольку это матрица 3×3. Следовательно, первое, что нам нужно сделать, это решить определитель всей матрицы (с помощью правила Сарруса), чтобы увидеть, может ли он иметь ранг 3:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fec1cb52bb87fa2bccb40b70e1f21c7c_l3.png)
Мы устанавливаем результат равным 0, чтобы увидеть, когда массив будет иметь ранг 2, а когда — 3:
![]()
Это неполное квадратное уравнение, поэтому выделим общий множитель:
![]()
И мы устанавливаем каждое слагаемое равным 0:
![Rendered by QuickLaTeX.com \displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43b38da320da538e46c6b4515de48568_l3.png)
В качестве решений мы получили 0 и -4. Поэтому, когда
![]()
отличается от 0 и -4, определитель 3×3 будет отличаться от 0 и, следовательно, ранг матрицы будет равен 3.
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d97b25f01cb00d4677da0de5b4340ddb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0f3c315588dff8274873001f727a69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c132b22650c707d9f410c3d9c1e8da35_l3.png)
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ce7e40d9d78ecddc5ee81fc799c8767_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-52d15d0bceeb1dbbc415fb4825ce9a05_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d45971f1dbda32405246de38bb68bd92_l3.png)
![]()
Таким образом, мы обнаружили 3 случая, в которых диапазон матрицы A меняется в зависимости от значения, которое принимает параметр:
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-844f152985a2d84be1456501dfdc16e4_l3.png)
Упражнение 4
Найдите размер следующей матрицы размером 3×4 в соответствии со значением параметра
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4da7907bd0e8f80006ea47d2437b3f3d_l3.png)
Матрица A будет иметь не более 3-го ранга, поскольку мы не можем вычислить какой-либо определитель 4×4 . Следовательно, первое, что нам нужно сделать, это найти все возможные определители порядка 3 (с помощью правила Сарруса), чтобы увидеть, может ли он быть порядка 3:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2db025b8ecf4323d4a912d84a215d8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e40592bf6f8bfd13cb68a1fd0393cebb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce1c28ae4120f0b37059b763e576d2eb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-668e9096b00b90ee4cc48d272b17e7bd_l3.png)
Результаты всех возможных определителей порядка 3 равны 0, независимо от значения
![]()
. Таким образом, матрица никогда не будет ранга 3, поскольку не имеет значения, какое значение она принимает.
![]()
что никогда не будет определителя 3×3, отличного от 0.
Итак, теперь мы пробуем определители размерности 2 × 2. Однако все определители порядка 2 также дают 0, за исключением следующих:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4408f1ccf562196943209356e50e892_l3.png)
Теперь приравниваем результат к 0 и решаем уравнение:
![]()
![]()
![]()
Поэтому, когда
![]()
отличается от -2, определитель 2×2 будет отличен от 0 и, следовательно, ранг матрицы будет равен 2.
![]()
Теперь посмотрим, что произойдет, когда
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ecbf63b188b46c05e67741cee83d7a2_l3.png)
Как мы видели ранее, когда
![]()
равно -2, все определители порядка 2 равны 0. Поэтому он не может иметь ранг 2. И поскольку существует хотя бы один определитель 1×1, отличный от 0, в этом случае ранг матрицы равен 1:
![]()
Таким образом, мы обнаружили 2 случая, в которых диапазон матрицы A меняется в зависимости от значения, которое принимает параметр:
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-2bdfb67894431a4a08a3e791dcda0313_l3.png)