В этой статье мы объясним, как получить произведение двух функций (формула). Кроме того, вы сможете увидеть несколько примеров производных произведений функций и даже потренироваться с решением упражнений на производные умножения.
Формула производной произведения
Производная произведения двух разных функций равна произведению производной первой функции на вторую недифференцированную функцию плюс произведение первой недифференцированной функции на производную второй функции.
Другими словами, если f(x) и g(x) — две разные функции, формула производной умножения между двумя функциями выглядит следующим образом:
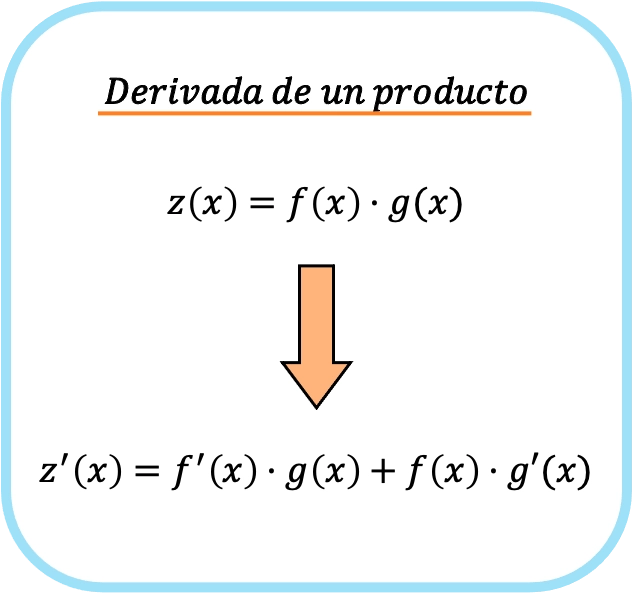
Таким образом, применяя правило производной произведения, мы переходим от простого умножения к двум различным произведениям.
Примеры производных продукта
Как только мы узнаем, какова формула производной произведения (или умножения), мы решим несколько примеров производной этого типа. Это облегчит вам понимание того, как получается произведение двух функций.
Пример 1
В этом примере мы решим производную двух потенциальных функций путем умножения:
![]()
Как мы видели в предыдущем разделе, формула производной умножения имеет вид:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
Поэтому надо сначала вычислить производную каждой функции отдельно:
![]()
![]()
И как только мы узнаем производную каждой функции, мы можем применить формулу производной произведения двух функций. То есть мы умножаем производную первого множителя на второй множитель, не дифференцируя, затем складываем произведение первого множителя, не дифференцируя, на производную второго множителя:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00f424cf1f72c1d3822c14d49873253e_l3.png)
Наконец, проведем операции по упрощению полученного результата:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-48b8d455b68b87932ca3a437f5ffe3a3_l3.png)
Пример 2
В этом случае мы выведем произведение константы на функцию:
![]()
Производное правило произведения выглядит следующим образом:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
Таким образом, мы отдельно выводим каждую функцию, входящую в состав произведения:
![]()
![]()
А затем применяем правило для производной от умножения:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c2d81edaa002aeb66ca6eec22bec001_l3.png)
Обратите внимание, что производная константы всегда равна нулю, поэтому мы можем сделать вывод, что производная от умножения константы на функцию равна произведению константы и производной функции.
![]()
Пример 3
Давайте решим произведение показательной функции на натуральный логарифм:
![]()
Формула производной от произведения двух функций:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
Поэтому мы должны сначала отдельно вывести производную каждой функции, образующей произведение, а именно:
![]()
![]()
Таким образом, производное произведение функций равно:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e1cb417a69252fe05883f7963bcb8db_l3.png)
Решенные упражнения на производную произведения
Выводит следующие функциональные продукты:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f46e303cda3be6c3781f7ee4c46c1680_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5dbaa6f333ff27c717b6478d26154025_l3.png)
Получено из трехфункционального продукта
Далее мы оставляем вам формулу производной от умножения трех функций, поскольку она очень похожа на формулу для двух функций и может быть полезна в некоторых случаях.
Производная произведения трех функций равна произведению производной первой функции и двух других функций плюс произведение производной второй функции и двух других функций плюс произведение производной третья функция.функция двумя другими функциями.
![]()
Например, если мы хотим получить следующее умножение трех разных функций:
![]()
Для решения производной необходимо применить правило производной произведения трех функций, следовательно:
![]()
Демонстрация формулы производной продукта
Наконец, мы продемонстрируем формулу производной умножения. Вам не обязательно запоминать их, но всегда полезно понять, откуда берутся формулы. 🙂
Из математического определения производной:
![]()
Пусть функция z является произведением двух разных функций:
![]()
Тогда производная от z , согласно определению, будет равна:
![]()
![]()
Как мы знаем, если мы добавим член путем сложения и вычитания, это не повлияет на результат, если оба термина являются одним и тем же. Поэтому мы можем перейти к следующему шагу:
![]()
Теперь мы используем свойства границы, чтобы разделить предыдущую границу на две разные границы:
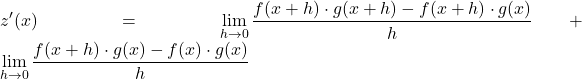
Выделим общий делитель в числителе двух дробей:
![]()
С другой стороны, мы знаем результат следующего предела:
![]()
Поэтому мы можем упростить ограничения:
![]()
![]()
Наконец, если посмотреть на два оставшихся предела, каждый соответствует определению производной функции. Таким образом, равенство можно упростить:
![]()
Или эквивалент:
![]()