Производная частного (деление): формула и решаемые упражнения

В этой статье мы объясним, как получить частное (или деление) двух функций. Вы найдете примеры производных частных функций и, кроме того, сможете попрактиковаться с помощью пошаговых упражнений на производные деления.

Формула производной частного

Производная коэффициента (или деления) функций идентична производной функции числителя на функцию знаменателя, меньшему, чем функция числителя на производную функции знаменателя, разделенную на квадрат функции старшего знаменателя.

формула производной деления или частного

Как видите, когда мы применяем правило для производной частного (или деления), после дифференцирования у нас все еще остается дробь. Но, кроме того, в числителе у нас два умножения и вычитание, а знаменатель возведен в степень двойки.

Примеры производных частных

Мы только что увидели, какова формула производной частного двух функций, затем решим несколько примеров производных такого типа операций. Помните: если вы не понимаете, как получается функциональное частное, вы можете задать нам вопрос в разделе комментариев.

Пример 1

В этом примере мы выведем потенциальную функцию, разделенную на тригонометрическую функцию:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

Формула производной от деления двух разных функций выглядит следующим образом:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Итак, нам сначала нужно вычислить производную каждой функции отдельно:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

Таким образом, производная всей функции равна:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Пример 2

В этом случае мы найдем производную константы, разделенную на функцию:

$f(x)=\cfrac{10}{x^2+3x-9}$

Как мы видели выше, правило для производной от деления двух разных функций следующее:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Итак, вычисляем производную числителя и знаменателя отдельно:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

И, наконец, находим производную от целочисленного деления:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

Фактически, мы можем вывести формулу для непосредственного дифференцирования, когда у нас есть константа в числителе, разделенная на функцию, поскольку производная константы всегда равна 0. Следовательно, следующая формула всегда будет верна:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Пример 3

В этом упражнении мы выведем частное двух многочленов:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Чтобы решить производную, мы должны применить правило для производной частного двух разных функций, которое выглядит следующим образом:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Теперь найдем производную полинома числителя и полинома знаменателя:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

Таким образом, производная от деления полинонимов равна:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

И наконец, проводим операции и максимально упрощаем дробь:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Решенные упражнения на производную частного

Выведите следующие подразделения функций:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Посмотреть решение

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Демонстрация производной частного

Наконец, мы продемонстрируем формулу производной от деления. Для этого воспользуемся общим определением производной, которое звучит так:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Пусть z — деление двух разных функций:

$z(x)=\cfrac{f(x)}{g(x)}$

Тогда производная функции z с применением математического определения будет равна:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

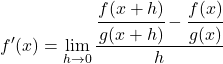
Решаем вычитание дробей из числителя дроби:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

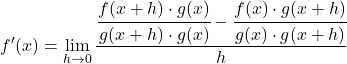
Добавление в уравнение членов сложения и вычитания не меняет уравнение. Поэтому мы можем перейти к следующему шагу:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

Выделим общий множитель:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Теперь перенесем член h из знаменателя в числитель, используя свойства дробей:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

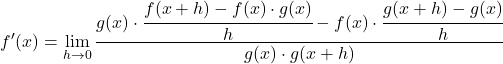
Преобразуем уравнение, применив свойства пределов:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

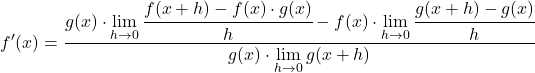
Пределы числителя точно соответствуют математическому определению производной каждой функции, поэтому:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

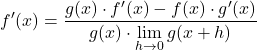
Решаем предел знаменателя дроби:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

И таким образом демонстрируется формула производной частного двух функций:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

Производная частного (или деления)

Формула производной частного

Примеры производных частных

Пример 1

Пример 2

Пример 3

Решенные упражнения на производную частного

Демонстрация производной частного

Оставьте комментарий Отменить ответ