Здесь вы найдете формулу производной арккотангенса и на примерах объясним, как вывести арккотангенс функции.
формула производной арккотангенса
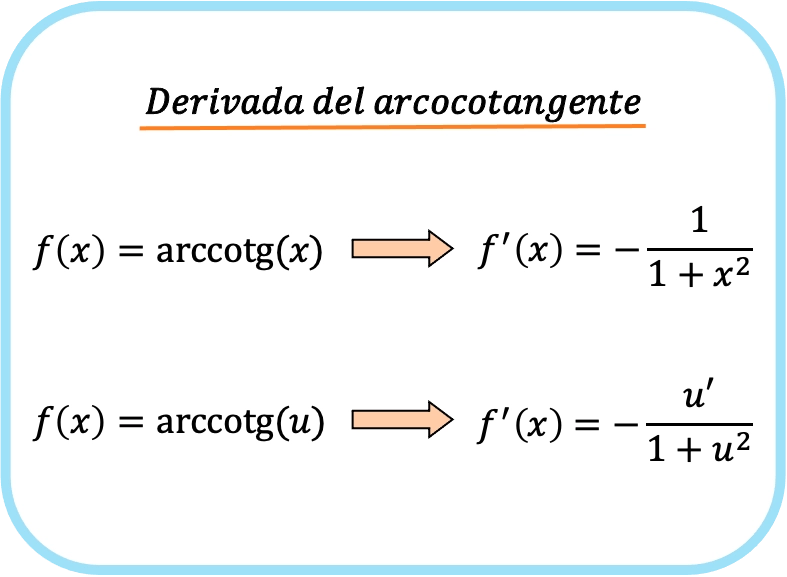
Производная арктангенса x равна отрицательной единице, разделенной на единицу плюс x в квадрате.
![]()
Следовательно, производная арккотангенса функции равна минус производной этой функции, деленной на единицу, плюс квадрат функции.
![]()
Обратите внимание, что первая и вторая формулы одинаковы, с той лишь разницей, что ко второму выражению применяется правило цепочки. Фактически, если вы подставите x вместо u, вы получите первую формулу, поскольку производная функции x равна 1.
Хотя арккотангенс является обратной функцией котангенса, их производные совершенно различны. Фактически, котангенс функции можно получить тремя способами, вы можете увидеть их все здесь:
➤ См.: формула производной котангенса
Примеры производной арккотангенса
После того, как вы увидели формулу производной арккотангенса, вот два решенных упражнения для этого типа тригонометрической производной. Также помните, что если у вас есть вопросы, вы можете оставить свой вопрос ниже в комментариях.
Пример 1
На этом примере мы увидим, сколько составляет производная арккотангенса квадратичной функции x 2 .
![]()
В аргументе арккотангенса у нас есть функция, отличная от x, поэтому нам нужно применить формулу для производной арккотангенса с цепным правилом:
![]()
Производная от x, возведенная в два раза, равна 2x, поэтому в числителе надо поставить 2x, а в знаменателе функцию возведенного в квадрат аргумента:
![]()
Пример 2
Во втором примере мы выведем арккотангенс полиномиальной функции третьей степени.
![]()
Для его вывода мы используем правило производной арккотангенса:
![]()
Таким образом, производная арккотангенса функции равна:
![]()