В этой статье мы объясним, как получить гиперболический арккосеканс функции. Вы также найдете рабочие примеры производной гиперболического арккосеканса.
Формула производной гиперболической косекансной дуги
Производная дугового гиперболического косеканса x равна минус 1, деленной на произведение x, умноженное на корень из единицы плюс x в квадрате.
![]()
Следовательно, производная дугового гиперболического косеканса функции равна минус производной указанной функции, деленной на произведение функции, умноженное на корень из единицы, плюс квадрат функции.
![]()
Вкратце, формула для расчета производной гиперболической функции арккосеканса выглядит следующим образом:
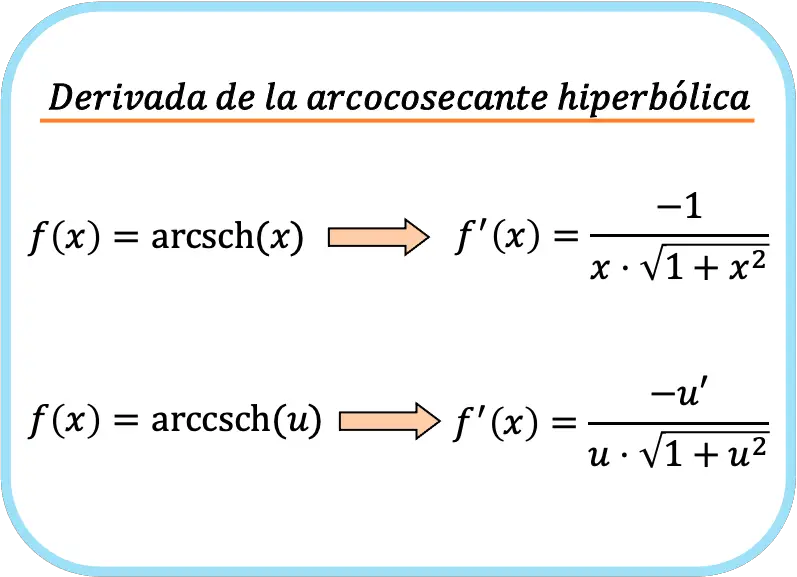
Хоть мы и привели две формулы, это не значит, что они разные. Если присмотреться, вторая формула аналогична первой, но с применением правила цепочки.
Примеры производной гиперболической косекансной дуги
Учитывая формулу производной косеканса гиперболической дуги, мы затем выведем две такие функции, чтобы вы могли увидеть, как это делается.
Пример 1
![]()
В этом упражнении мы должны использовать формулу производной гиперболического косеканса дуги с цепным правилом, поскольку в аргументе присутствует функция, отличная от x:
![]()
Итак, чтобы найти производную, нам нужно заменить u на 3x, а u’ на ее производную, которая равна 3:
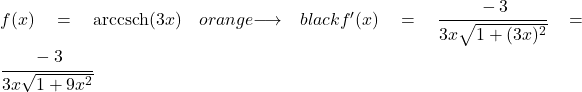
Пример 2
![]()
В этом случае у нас есть полиномиальная функция в аргументе гиперболического арккосеканса, поэтому нам также нужно использовать цепное правило для ее получения:
![]()
Поэтому в числитель дроби ставим производную функции аргумента, а в знаменателе меняем u на полиномиальную функцию:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)
Похожие товары
- Производная гиперболического арккосинуса
- Производная гиперболического косеканса
- Производная гиперболического косинуса
- Производная косекансной дуги
- полученное из косеканса
- Производная арккосинуса
- производная косинуса