Здесь мы объясним, как получить гиперболический котангенс функции. Вы также найдете примеры производной гиперболического котангенса.
Формула производной гиперболического котангенса
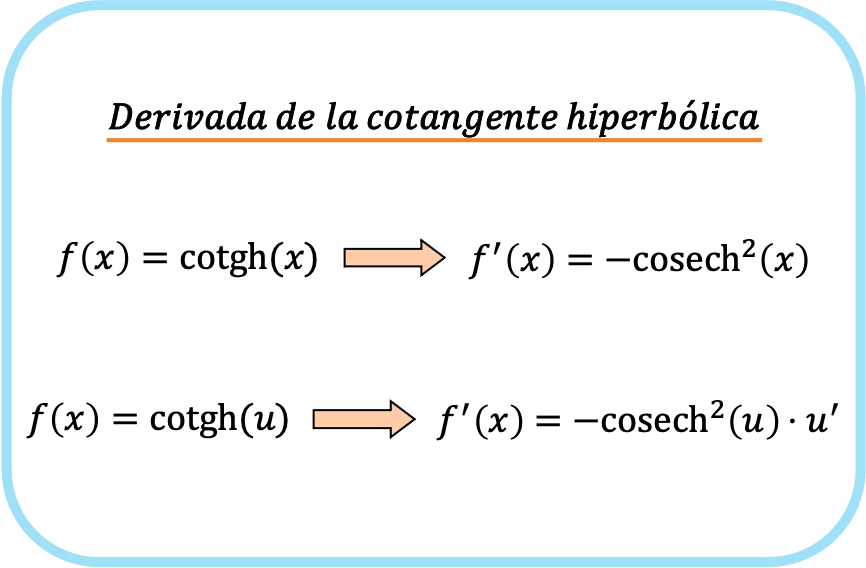
Производная гиперболического котангенса x равна минус гиперболическому косекансу x в квадрате.
![]()
Следовательно, производная гиперболического котангенса функции равна минус гиперболическому косекансу функции, умноженному на производную этой функции.
![]()
Имейте в виду, что во второй формуле было применено цепное правило, и эта формула используется, когда в аргументе гиперболического котангенса присутствует функция, отличная от x.
В некоторых книгах по математике вы можете найти, что производная котангенса другая, поскольку следующие три выражения эквивалентны:
![]()
Очевидно, что для получения гиперболического котангенса вы можете использовать любое выражение из трех, которое вам больше нравится, но наиболее часто используемым является квадрат гиперболического косеканса.
Примеры производной гиперболического котангенса
Как только мы узнаем, какова формула производной гиперболического котангенса функции, мы решим несколько примеров тригонометрических производных этого типа.
Пример 1
В этом примере мы увидим, что является производной гиперболического котангенса функции 2x.
![]()
В аргументе гиперболического котангенса у нас есть функция, отличная от x, поэтому нам нужно использовать формулу с правилом цепочки для вывода:
![]()
Поскольку 2x — член первой степени, его производная равна 2. Итак, чтобы найти производную гиперболического котангенса 2x, мы просто подставляем 2x в квадрат аргумента гиперболического косеканса и умножаем на 2.
![]()
Пример 2
Во втором примере мы определим значение производной гиперболического котангенса полиномиальной функции.
![]()
Как мы видели выше, правило определения гиперболического котангенса функции следующее:
![]()
Следовательно, производная гиперболического котангенса этого упражнения будет следующей:
![]()