Производная гиперболического арктангенса

Здесь вы узнаете, как вывести гиперболический арктангенс функции. Вы также сможете увидеть решенные примеры тригонометрических производных этого типа и, наконец, мы покажем вам формулу производной гиперболического арктангенса.

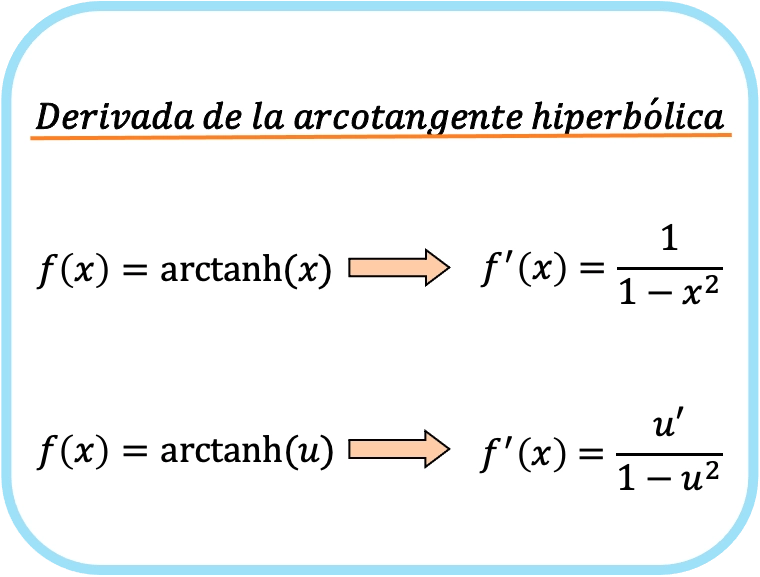
Формула производной гиперболического арктангенса

Производная гиперболического арктангенса x равна единице минус x в квадрате.

$f(x)=\text{arctanh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}$

Следовательно, производная гиперболического арктангенса функции равна частному производной этой функции, деленному на единицу минус указанная функция в квадрате.

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

По сути, обе формулы одинаковы, но во второй применяется правило цепочки. Например, замена x на u дает нам в точности первую формулу, поскольку производная x равна 1.

производная гиперболического арктангенса

Точно так же, как арктангенс является обратной функцией тангенса, гиперболический арктангенс является обратной функцией гиперболического тангенса. Несмотря на это, их производные очень разные, вы можете проверить производную этой тригонометрической функции здесь:

➤ См.: формула производной гиперболического тангенса

Примеры производной гиперболического арктангенса

Пример 1

$f(x)=\text{arctanh}(2x)$

По логике вещей мы должны применить правило производной гиперболического арктангенса:

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

Производная 2х равна 2, поэтому в числителе дроби поставьте двойку, а в знаменателе — единицу минус 2х в квадрате:

$f(x)=\text{arctanh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1-(2x)^2}}=\cfrac{2}{1- 4x^2}$

Пример 2

$f(x)=\text{arctanh}(e^{3x})$

Чтобы найти производную этой функции, нам нужно использовать формулу производной гиперболического арктангенса.

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

Кроме того, функция аргумента гиперболического арктангенса является составной функцией, поэтому нам также потребуется применить цепное правило:

$f(x)=\text{arctanh}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}$

Доказательство производной гиперболического арктангенса

В этом последнем разделе мы продемонстрируем формулу производной гиперболического арктангенса.

$y=\text{arctanh}(x)$

Поскольку гиперболический арктангенс является обратным гиперболическим тангенсом, мы можем выразить предыдущее равенство по-другому:

$x=\text{tanh}(y)$

Теперь продифференцируем обе части уравнения:

$1=\cfrac{1}{\text{cosh}^2(y)}\cdot y'$

Мы очищаем вас:

$y'=\text{cosh}^2(y)$

С другой стороны, мы знаем, что разница квадратов гиперболического косинуса и гиперболического синуса дает 1. Поэтому мы можем преобразовать предыдущее выражение в дробь:

$\text{cosh}^2(y)-\text{senh}^2(y)=1$

$y'=\cfrac{\text{cosh}^2(y)}{1}=\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)-\text{senh}^2(y)}$

Все члены дроби разделим на квадрат гиперболического косинуса:

$y'=\cfrac{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}}{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}$

$y'=\cfrac{1}{1-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}$

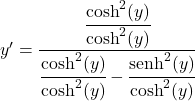
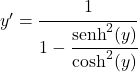
Частное гиперболического синуса между гиперболическим косинусом равно гиперболическому тангенсу, следовательно:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

$y'=\cfrac{1}{1-\text{tanh}^2(y)}$

Но, как мы видели в начале доказательства, гиперболический тангенс эквивалентен переменной x, поэтому мы можем подставить выражение, получив таким образом формулу для производной гиперболического арктангенса:

$y'=\cfrac{1}{1-x^2}$

Производная гиперболического арктангенса

Формула производной гиперболического арктангенса

Примеры производной гиперболического арктангенса

Пример 1

Пример 2

Доказательство производной гиперболического арктангенса

Похожие товары

Оставьте комментарий Отменить ответ