В этой статье мы объясним, как получить гиперболический арккотангенс функции. Кроме того, вы сможете увидеть решенные примеры производной гиперболического арккотангенса.
Формула производной гиперболического арккотангенса
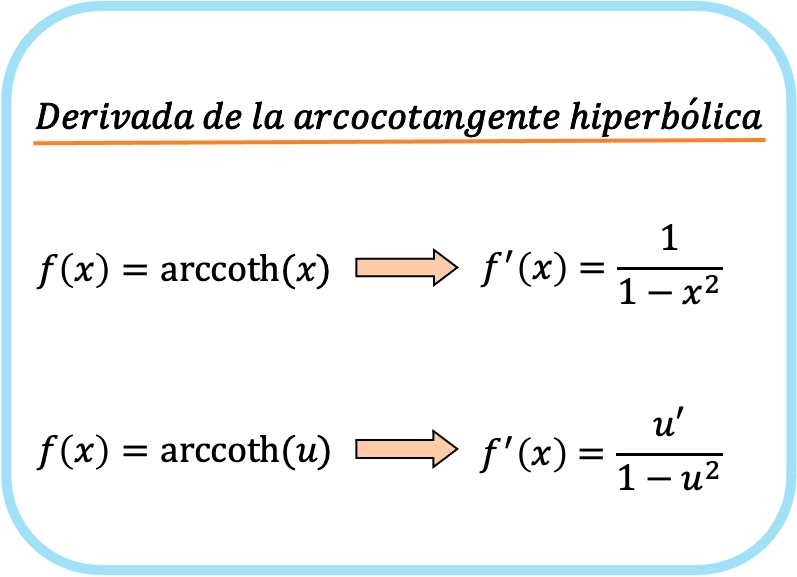
Производная гиперболического арккотангенса x равна единице минус x в квадрате.
![]()
Следовательно, производная гиперболического арккотангенса функции равна частному производной этой функции, деленному на единицу минус квадрат этой функции.
![]()
Обратите внимание, что вторая формула похожа на первую, но применяет правило цепочки, поэтому их фактически можно считать одной и той же формулой.
В некоторых учебниках по математике вы можете увидеть, что производная обратной тригонометрической функции этого типа равна:
![]()
Однако, если присмотреться, это одна и та же формула, с той лишь разницей, что числитель и знаменатель дроби умножены на -1.
Примеры производной гиперболического арккотангенса
Пример 1
![]()
В аргументе гиперболического арккотангенса у нас есть функция, отличная от x, поэтому нам нужно использовать формулу цепного правила для ее получения:
![]()
Производная 5х равна 5, поэтому в числителе дроби поставьте 5, а в знаменателе поставьте минус 5х в квадрате:
![]()
Пример 2
![]()
Чтобы найти производную этой функции, нам нужно применить формулу для производной гиперболического арккотангенса, которая выглядит следующим образом:
![]()
В данном случае мы имеем составную функцию, так как в аргументе тригонометрической функции имеется показательная функция. Поэтому нам нужно использовать цепное правило, чтобы найти производную всей функции:
![]()
Похожие товары
- Производная гиперболического арктангенса
- Производная гиперболического тангенса
- Производная гиперболического котангенса
- Производная арккотангенса
- Производная арктангенса
- полученное из котангенса
- производная тангенса