На этой странице вы найдете объяснение подобных матриц, также называемых подобными матрицами. Более того, мы покажем вам наглядный пример двух подобных матриц и все свойства этого типа матриц, чтобы у вас не осталось сомнений. Наконец, вы даже сможете увидеть, как они соотносятся с конгруэнтными матрицами.
Что такое подобные (или подобные) матрицы?
Определение подобных матриц следующее:
две матрицы
И
подобны (или подобны), если существует матрица
при котором выполняется следующее условие:
Или эквивалент:
Фактически, матрица
действует как матрица изменения базиса. Следовательно, это уравнение означает, что матрица
можно выразить в другой базе (
), что порождает матрицу
.
Этот термин также можно назвать преобразованием подобия , поскольку мы фактически преобразуем матрицу
в матрице
.
Очевидно, что матрица
это должна быть правильная или невырожденная матрица (ненулевой определитель).
С другой стороны, мы можем указать, что две матрицы аналогичны следующему выражению:
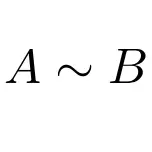
Этот класс матриц более важен, чем кажется для линейной алгебры. В основном они используются для диагонализуемых матриц, поскольку процедура диагонализации любой матрицы основана на понятии подобия матриц.
Фактически, процесс диагонализации матрицы включает в себя вычисление аналогичной матрицы, которая в то же время является диагональной матрицей. Вы можете увидеть, как это делается, в разделе «Как диагонализировать матрицу» .
Пример похожих или похожих матриц
Затем мы увидим пример подобных матриц размерности 2×2, чтобы завершить усвоение понятия.
- Квадратные матрицы A и B подобны друг другу обратимой матрицей P:
![\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4978e1117b69063b63256a0663eaf207_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6344f1d5a14dd381ab105bcb52827455_l3.png "Rendered by QuickLaTeX.com")
Чтобы показать, что это взаимно подобные матрицы, мы должны сначала вычислить обратную матрицу P:
![\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49a4a995246e782635e2e2b43302798_l3.png "Rendered by QuickLaTeX.com")
И теперь мы проверяем их схожесть, выполнив матричное произведение, определяющее сходство двух матриц:
✅
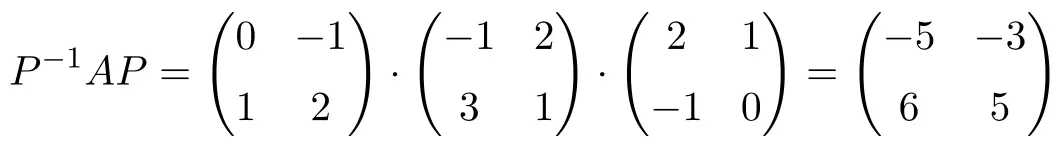
Да, соотношение подобия выполнено, значит, это подобные матрицы.
Похожие свойства матрицы
Две подобные матрицы A и B имеют следующие характеристики:
- Тот же ранг.
- Определители обеих матриц одинаковы.
- Та же самая трассировка.
- Те же собственные значения (или собственные значения). Однако собственные векторы (или собственные векторы) обычно различны.
- Тот же характеристический полином и минимальный полином.
- Транспонирование матрицы аналогично исходной матрице.
- Матрицу B можно найти, применяя элементарные операции к строкам матрицы A, и наоборот.
- Очевидно, сходство отражено. То есть, если А похоже на Б, то и Б похоже на А.
- При этом подобие матриц также симметрично. Другими словами, если с помощью матрицы P можно получить матрицу, подобную A(B), то матрицу, подобную B(A), можно получить и с той же матрицей P:
- Более того, сходство транзитивно. Таким образом, если матрица A похожа на матрицу B, а матрица B похожа на матрицу C, то матрица A также похожа на матрицу C.
![\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9f845ee4a4c9e72220ecb4033ea9640_l3.png "Rendered by QuickLaTeX.com")
- Наконец, каждая матрица похожа на пилообразную матрицу. И из этого свойства можно вывести следующее следствие: каждая квадратная матрица подобна треугольной матрице.
конгруэнтные матрицы
С другой стороны, существует еще одна очень похожая связь между матрицами, но она связана не с обратной матрицей, а с транспонированной матрицей. Это называется конгруэнтностью .
Две матрицы A и B конгруэнтны , если существует обратимая матрица P, для которой выполняется следующее равенство:
Как видите, это аналог аналогичных матриц, но с транспонированной матрицей.